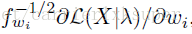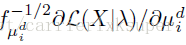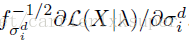我寫東西喜歡五顏六色，也喜歡通俗的來講！哈哈。。。。

核心：

Fisher vector本質上是用似然函式的梯度vector來表達一幅影象

基礎知識的預備：

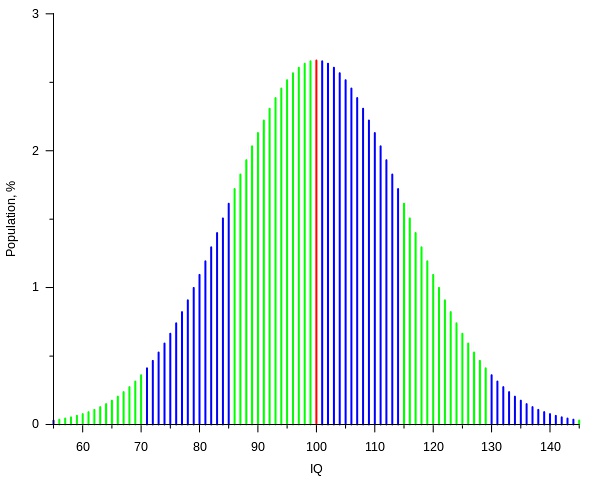
1. 高斯分佈

生活和自然中，很多的事和物的分佈都可以近似的看做是高斯分佈。比如說：一個班的成績的優良中差的分佈。最優秀的和最差的往往都是少數，一般人是大多數。

高斯分佈直觀的感受是這樣的：這是這種分佈的概率情況的表示：

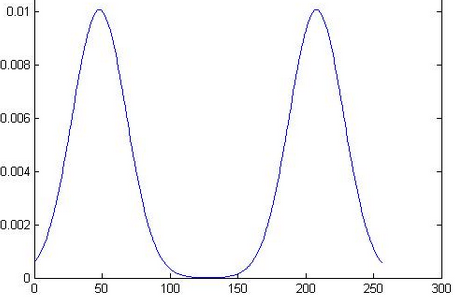
2. 混合高斯分佈

問題是：一個班的成績的分佈他也可能是這樣的：60分以下以及95分以上很少人，60-75很多人，突然75-85人又少了，但是85-90又多了。這個時候直觀的感受是這樣的：

這個時候很顯然若使用兩個高斯分佈來擬合，加上二者的權重效果比單個的高斯分佈要好得多！若是不止兩個山峰那最好就是再多幾個高斯的分佈同時來擬合。所以我對GMM（Gaussian Mixture Model）理解。

3.高斯分佈用於影象

相信大家對於獨立同分布（i.i.d）還是知道的。對於影象也是，它表示為你用來表示這樣影象的特徵的哥哥維度之間是獨立的。拿一個人來說，我們如果用它的身高、體重、三維來代替他。那這些就是他的特徵了。對於他來說，這些特徵就可以看做是獨立同分布了。對於一個影象同樣是這樣。

而用到獨立同分布最重要的原因是：你可以將一個樣本（一張圖片）的概率分佈表示為各個特徵維度上面的概率分佈的乘積。即： 取對數以後則表示為各項的對數概率的和，這樣就極大的降低了計算的難度。

嵌入在高維空間中的低維流形：最直觀的例子通常都會是嵌入在三維空間中的二維或者一維流行。比如說一塊布，可以把它看成一個二維平面，這是一個二維的歐氏空間，現在我們（在三維）中把它扭一扭，它就變成了一個流形（當然，不扭的時候，它也是一個流形，歐氏空間是流形的一種特殊情況）。所以，直觀上來講，一個流形好比是一個 d 維的空間，在一個 m 維的空間中 (m > d) 被扭曲之後的結果。

5. Fisher Vector 的本質

Fisher Vector的本質就是對於高斯分佈-的變數求偏導！也就是對權重，均值，標準差求編導得到的結果。最後在需要一個歸一化處理。具體的可以參照：

在此之前再定義一個變數：

，表徵的是occupancyprobability，也就是特徵xt是由第i個高斯分佈生成的概率。

下面的公式給出了偏導計算公式：

-------------------------------------4

     值得注意的是上面求出來的都是沒有歸一化的vector，需要進行歸一化操作，正如上一篇blog介紹的那樣，由於是在概率空間中，與歐式空間中的歸一化不同，引入Fisher matrix進行歸一化。

   公式4的三個變數分別引入三個對應的歸一化需要的fisher matrix：

------------------------------5

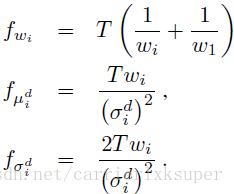
於是最終歸一化之後的fisher vector就是：

由於每一個特徵是d維的，需要K個高斯分佈的線性組合，有公式5，一個Fisher vector的維數為（2*d+1）*K-1維。

這樣得到的便是一張圖片的特徵了，便可以做視覺方面的操作勒。

6. 為什麼Fisher Vector比高斯分佈有效

我們將一張圖近似為一個高斯分佈，由這個高斯分佈來表示這張影象。假設我們是做目標的檢測，那麼當你得到一個有相同的高斯分佈的圖的時候你就可以判斷出這就是那個目標了。但實際的情況是卻不一定是這樣的，我們看一張圖：

這兩張圖上特徵點的分佈在黑色的區域，二者的分佈卻可以一樣（當然我畫的不是很好）！

由此，我們知道，在高斯分佈的基礎上我們再找到變化的方向，我們便可以更加準確的表示這一張圖！

我幾乎是從道理上講解的，細節還需要參考論文：Image Classification with the Fisher Vector: Theory and Practice. 等

好的，希望可以幫到你！

iker Cross

2014年12月2日