劍指offer:二叉搜尋樹與雙向連結串列(Python)
阿新 • • 發佈:2019-01-29
站在巨人的肩膀上,風景這邊獨好;
親自爬上巨人的肩膀,才知風景為什麼這麼美。
題目描述
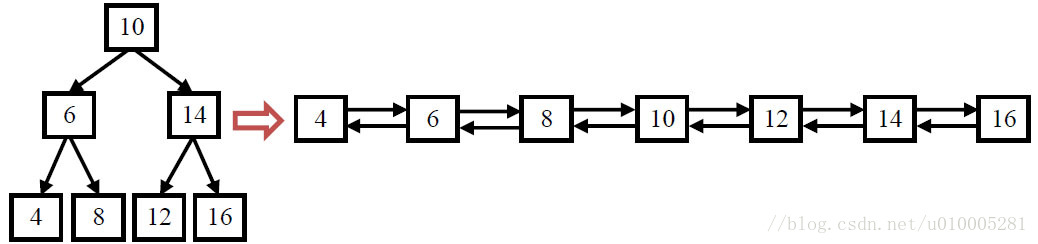
輸入一棵二叉搜尋樹,將該二叉搜尋樹轉換成一個排序的雙向連結串列。要求不能建立任何新的結點,只能調整樹中結點指標的指向。如圖:
解題思路
吐槽
我刷的牛客網就只有文字描述沒有圖啊!!表示看不懂… 網上搜索看到這張圖片之後開始構思解題思路。當時瞄到這麼一張圖:

然後就開始順著這張圖的思路想解決辦法了:用中序遍歷和遞迴,且以這張圖為第一步,後續的左右子樹均按照圖示的思路來做,並且前後不用任何中間節點。但慢慢發現,如果用遞迴,在不新建任何中間節點的情況下,我只能實現到:4==6==8==10==16==14==12,並且圖示提供的思路也不夠精確。
遂求助網路,但得到的解法均需要新建輔助節點,且絕大多數程式碼不夠簡練。在牛客網該題下 大家的討論中倒是有不錯的思路,只是沒有配文的情況下還需要點時間理解。鑑於自己沒查到該題精簡且詳細的解題思路,我就露個拙,實現Python解法,並配上我的理解。
思路
- 核心演算法依舊是中序遍歷
- 不是從根節點開始,而是從中序遍歷得到的第一個節點開始
- 定義兩個輔助節點listHead(連結串列頭節點)、listTail(連結串列尾節點)。事實上,二叉樹只是換了種形式的連結串列;listHead用於記錄連結串列的頭節點,用於最後演算法的返回;listTail用於定位當前需要更改指向的節點。瞭解了listHead和listTail的作用,程式碼理解起來至少順暢80%。
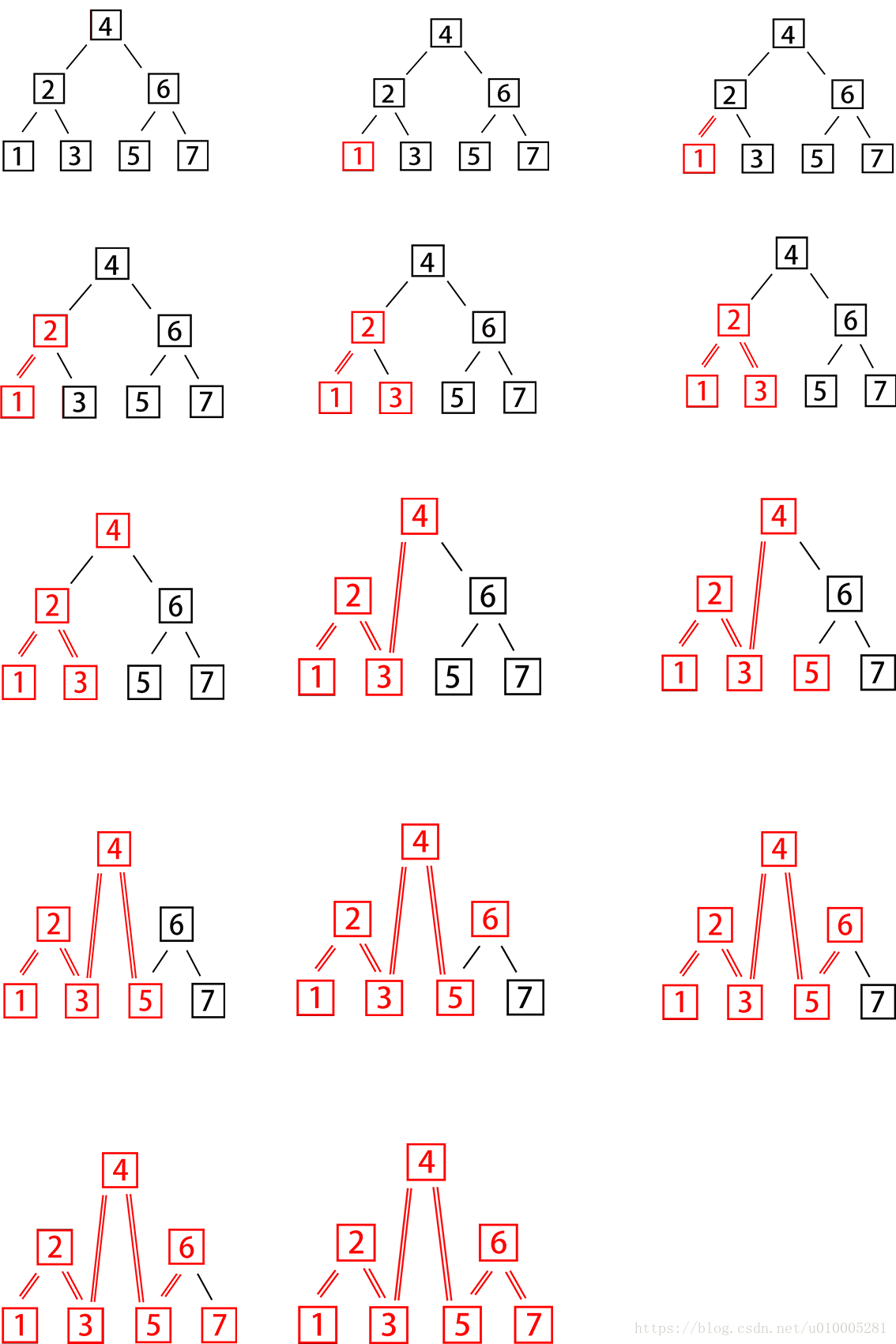
- 提供我畫的演算法的過程圖,有點醜,但有助於理解(幫你們畫了,你們就不用畫啦),另外圖中右上角步驟三應該是“2”標紅,“2”和“1”中間的連線為單線黑~~~
Python程式碼
class Solution:
def __init__(self):
self.listHead = None
self.listTail = None
def Convert(self, pRootOfTree):
if pRootOfTree==None:
return
self.Convert(pRootOfTree.left)
if self.listHead==None:
self.listHead = pRootOfTree
self.listTail = pRootOfTree
else 稍微多說一句,其實這段程式碼也就5行,5行中2行是中序遍歷的程式碼,分別是第8、16行;3行是更改節點指向的程式碼,為13-15行。9-11行的if語句只有在中序遍歷到第一個節點時呼叫,自此之後listHead不變,listTail跟隨演算法的進度。為了更清楚的展示,給出中序遍歷的程式碼如下。對比可以看出來,實際上只是中序遍歷中的第八行程式碼被上述的if-else語句替代了,僅此而已。
class Solution:
def __init__(self):
self.array = []
def midOrder(self, root):
if not root:
return self.array
self.midOrder(root.left)
self.array.append(root.val)
self.midOrder(root.right)不想一個節點一個節點的驗證得到的雙向連結串列是否正確,可以用如下方法驗證連結串列的正向序和反向序:
def printList(self, head):
while head.right:
print(head.val, end=" ")
head = head.right
print(head.val)
while head:
print(head.val, end= " ")
head = head.left最後的最後,寫程式碼一般需要在自己的編輯器上跑通,才會提交到網站上,所以這裡給出全套的程式碼,用以驗證方法的正確與否:
class Solution:
def __init__(self):
self.listHead = None
self.listTail = None
# 將二叉樹轉換為有序雙向連結串列
def Convert(self, pRootOfTree):
if pRootOfTree==None:
return
self.Convert(pRootOfTree.left)
if self.listHead==None:
self.listHead = pRootOfTree
self.listTail = pRootOfTree
else:
self.listTail.right = pRootOfTree
pRootOfTree.left = self.listTail
self.listTail = pRootOfTree
self.Convert(pRootOfTree.right)
return self.listHead
# 獲得連結串列的正向序和反向序
def printList(self, head):
while head.right:
print(head.val, end=" ")
head = head.right
print(head.val)
while head:
print(head.val, end= " ")
head = head.left
# 給定二叉樹的前序遍歷和中序遍歷,獲得該二叉樹
def getBSTwithPreTin(self, pre, tin):
if len(pre)==0 | len(tin)==0:
return None
root = TreeNode(pre[0])
for order,item in enumerate(tin):
if root .val == item:
root.left = self.getBSTwithPreTin(pre[1:order+1], tin[:order])
root.right = self.getBSTwithPreTin(pre[order+1:], tin[order+1:])
return root
class TreeNode:
def __init__(self, x):
self.left = None
self.right = None
self.val = x
if __name__ == '__main__':
solution = Solution()
preorder_seq = [4,2,1,3,6,5,7]
middleorder_seq = [1,2,3,4,5,6,7]
treeRoot1 = solution.getBSTwithPreTin(preorder_seq, middleorder_seq)
head = solution.Convert(treeRoot1)
solution.printList(head)
# 4
# / \
# 2 6
# / \ / \
# 1 3 5 7