題目描述：
輸入一顆二叉搜尋樹，將該二叉搜尋樹轉換成一個排序的雙向連結串列。要求不能建立新的結點，只能調整樹中結點指標的指向。

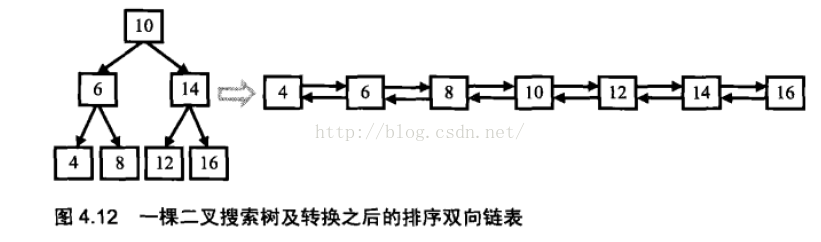
比如如下圖中的二叉搜尋樹，則輸出轉換之後的排序雙向連結串列為：

分析：

在二叉樹中，每個結點都有兩個指向子節點的指標。在雙向連結串列中，每個結點也有兩個指標，他們分別指向前一個結點和後一個結點。由於這兩種結點的結構相似，同時二叉搜尋樹也是一種排序的資料結構，因此在理論上有可能實現二叉搜尋樹和排序的雙向連結串列的轉換。在搜尋二叉樹中，左子結點的值總是小於父節點的值，右子節點的值總是大於父節點的值。因此我們在轉換成排序的雙向連結串列時，原先指向的左子結點的指標調整為連結串列中指向前一個結點的指標，原先指向右子節點的指標調整為連結串列中指向後一個結點的指標。接下來我們考慮如何轉化。

由於要求轉換之後的連結串列是排好序的，我們可以中序遍歷樹中的每一個結點，這是因為中序遍歷演算法的特點是按照從小到大的順序遍歷二叉樹的每一個結點。當遍歷到根節點的時候，我們把樹分為三部分：值為10的結點，根節點為6的左子樹、根節點為14的右子樹。根據排序連結串列的定義，值為10的結點將和它的左子樹的最大的一個結點（即值為8的結點）連線起來，同時它還將右子樹最小的結點（即值為12的結點）連線起來，如圖：

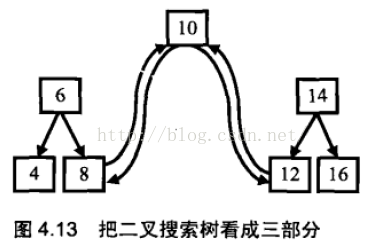
按照中序遍歷的順序，當我們遍歷轉換到根節點（值為10的結點）時，它的左子樹已經轉換成一個排序的連結串列了，並且處在連結串列中的最後一個結點是當前值的最大的結點。我們把值為8的結點與根節點連結起來，此時連結串列中的最後一個結點是10了。接著我們去遍歷轉換右子樹，並把根節點和右子樹最小的結點連結起來。至於怎麼去轉換它的左子樹和右子樹，由於遍歷和轉換過程是一樣的，我們自然的想到了遞迴。

程式碼如下：

/**
 * 二叉搜尋樹轉換成排序的雙向連結串列
 */
public class BinaryTreeConvert {

    public BinaryTreeNode convert(BinaryTreeNode root) {
        //指向雙向連結串列的尾節點
        BinaryTreeNode lastNodeInList = null;
        convertNode(root, lastNodeInList);

        //我們需要返回頭結點
        BinaryTreeNode head = lastNodeInList;
        while
 
(head != null && head.left != null){
            head = head.left;
        }
        return head;
    }

    //使用遞迴進行轉換
    public void convertNode(BinaryTreeNode node, BinaryTreeNode lastNodeInList) {
        if(node == null)
            return ;

        BinaryTreeNode currentNode = node;
        if(currentNode.left != null){
            convertNode(currentNode.left, lastNodeInList);
        }
        currentNode.left = lastNodeInList;
        if(lastNodeInList != null){
            lastNodeInList.right = currentNode;
        }
        lastNodeInList = currentNode;
        if(currentNode.right != null){
            convertNode(currentNode.right, lastNodeInList);
        }
    }

}

//二叉樹節點
class BinaryTreeNode {
    int value;
    BinaryTreeNode left;
    BinaryTreeNode right;
}