基於Mathematica的機器人模擬環境(機械臂篇)
目的
本文手把手教你在 Mathematica 科學計算軟體中搭建機器人的模擬環境,具體包括以下內容:
1 匯入機械臂的三維幾何模型
2 正\逆運動學模擬
3 碰撞檢測
4 軌跡規劃
5 正\逆動力學模擬
6 運動控制
文中的程式碼和模型檔案點選此處下載。使用的軟體版本是 Mathematica 11.1,較早的版本可能缺少某些函式,所以最好使用最新版。進入正文之前不妨先看幾個例子:




無論你從事的是機器人研發還是教學科研,一款好用的模擬軟體都能對你的工作起到很大的幫助。那麼應該選擇哪個軟體呢?最方便的選擇就是成熟的商業軟體,例如Adams、RecurDyn、Webots。你的錢不是白花的,商業軟體功能強大又穩定,而且效能一般都經過了優化。可是再強大的商業軟體也有設計不合理的地方,它們的演算法基本都是“黑箱”,你想做一點更改都不行。從學習和研究的角度出發,最好選擇程式碼可修改的開源或半開源軟體。
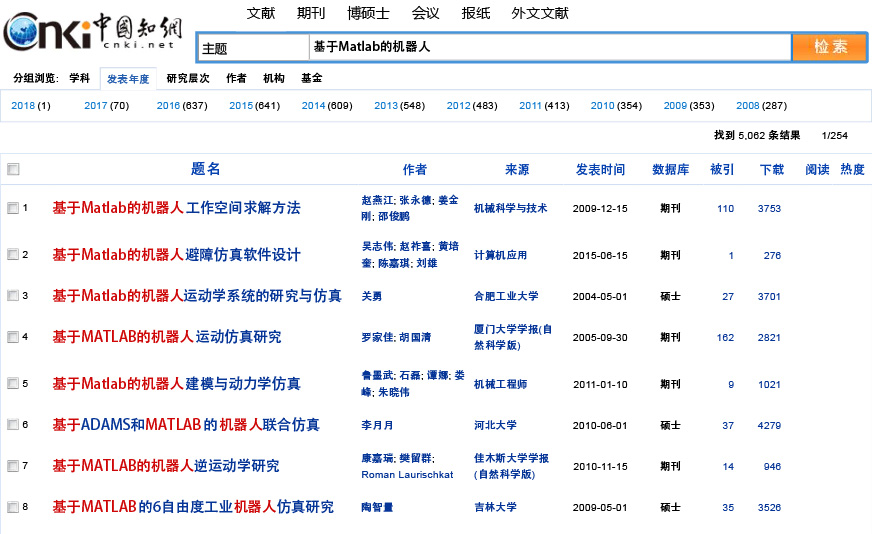
在論文資料庫中檢索一下就會發現,很多人都選擇藉助Matlab這個通用軟體平臺進行機器人的建模模擬。這並不奇怪,因為Matlab具有優秀的數值計算和模擬能力,在它的基礎上開發會很便利。如果你非要捨近求遠,用 C++ 編寫一套模擬軟體,先不要說模擬結果如何顯示,光是矩陣計算的實現細節就能讓你焦頭爛額。
| Matlab | Mathematica | |
| 視覺化效果 |
一般 | 優秀 |
| 匯入機器人模型 | 需要自己寫函式 | 自帶函式 |
| 機器人工具箱/包 | Robotic Toolbox、SpaceLib等 | Screws、Robotica等 |
| 除錯功能 | 方便易用 | 目前還不太方便,有點繁瑣 |
| 程式碼長度(個人經驗) |
1. 獲取機器人的外觀模型
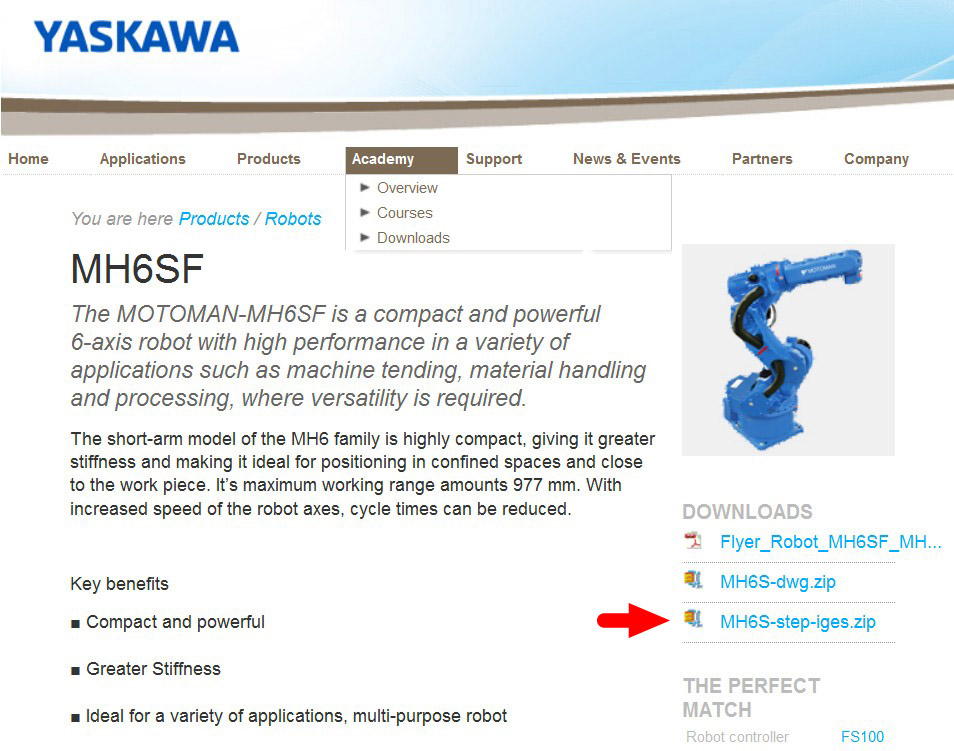
製作逼真的模擬首先需要的是機器人的外觀模型。如果你有機器人的三維模型最好,沒有的話也不要緊,著名的機器人制造商都在官網提供其各種型號機器人的真實模型,例如 ABB、安川,供大家免費下載和使用。
說明:為了防止山寨或者篡改,這些模型都是不可通過建模軟體修改的格式,例如 IGES 和 STEP 格式。但我們只用來顯示和碰撞檢測,所以並不影響模擬。
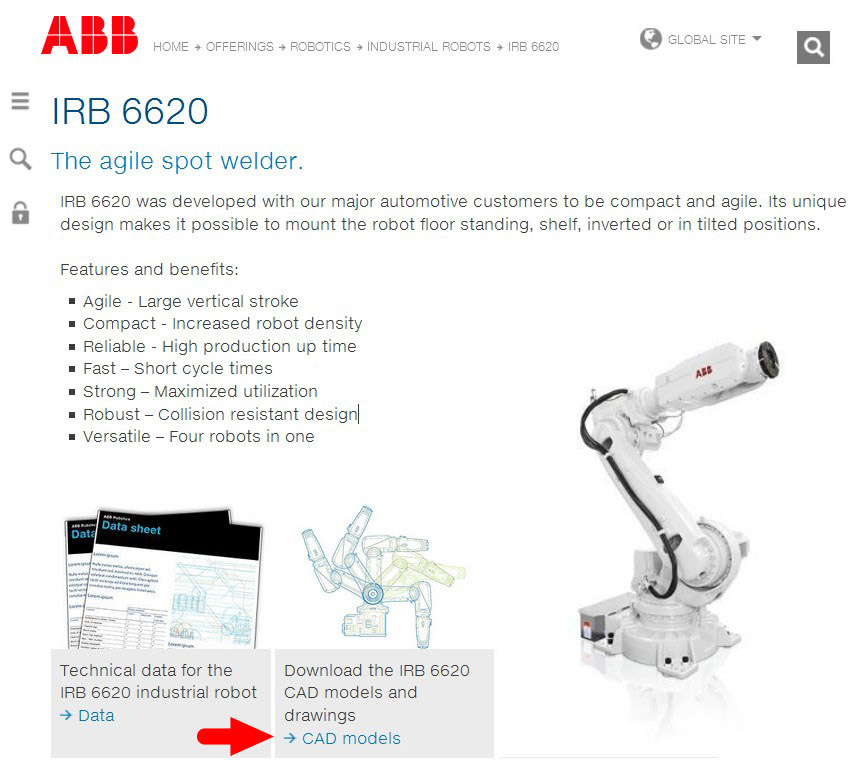
2. 匯入機器人的外觀模型
獲得模型後要匯入Mathematica中進行處理並顯示,下面我們藉助一個例子說明具體的步驟。Motoman ES165D 是安川公司生產的一款6自由度點焊機器人,其最後三個關節軸線相交於一點,這是一種非常經典而且有代表性的設計,因此我們選擇以這款機器人為例進行講解(這個機器人的完整模型點選此處下載)。

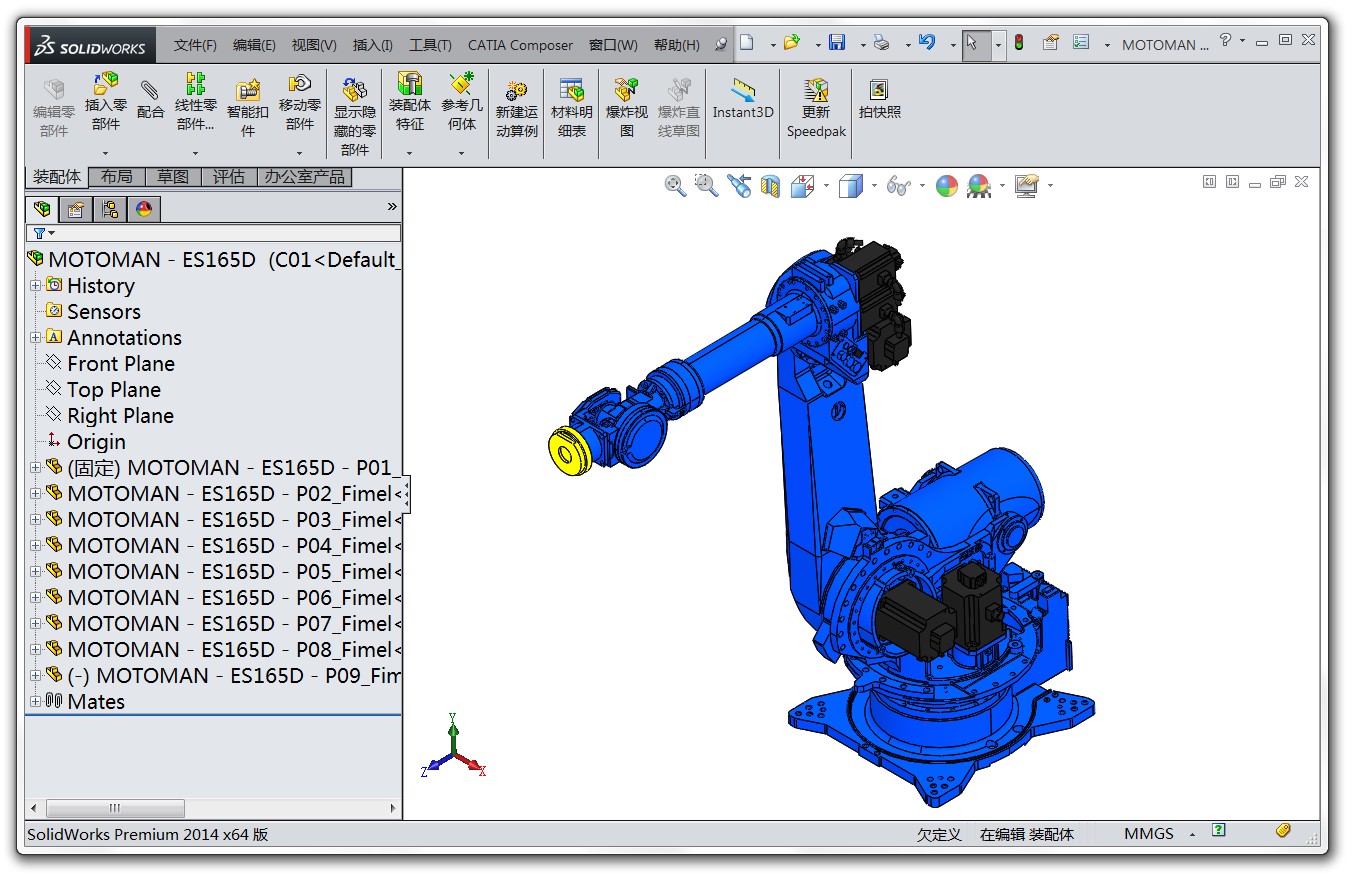
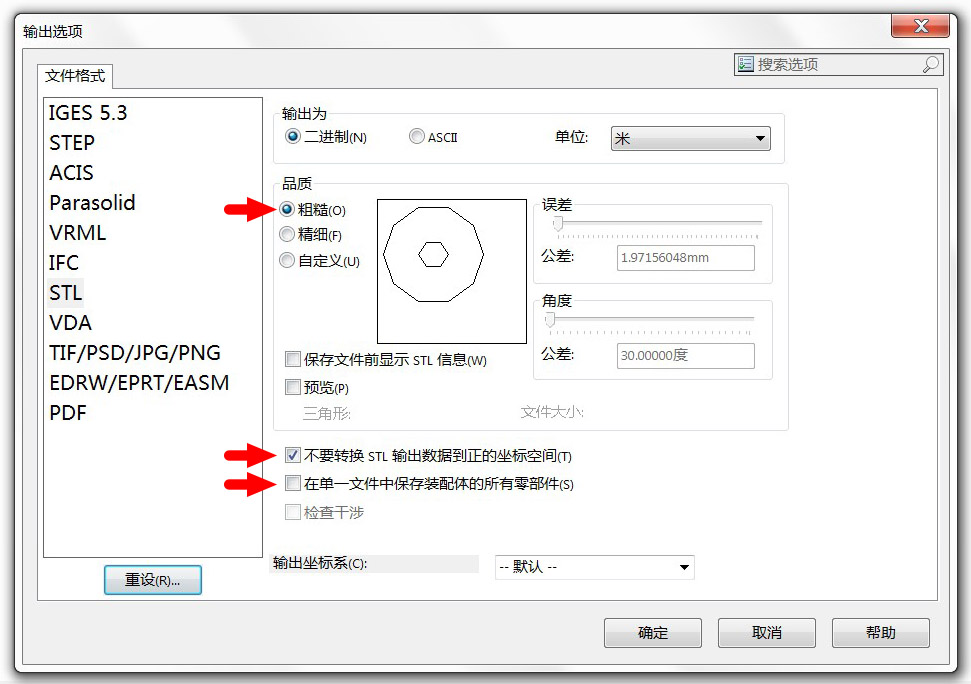
用SolidWorks 2014軟體開啟機器人的裝配體檔案,並選擇“另存為”STL 格式。然後開啟當前頁面下方的“選項”對話方塊,如下圖。這裡我們要設定三個地方:
1. “品質”表示對模型的簡化程度,如果你想實現非常逼真的效果,可以選擇“精細”,但缺點是資料點很多導致檔案很大、處理起來比較慢。一般選擇“粗糙”就夠了;
2. 勾選“不要轉換 STL 輸出資料到正的座標空間”;
3. 不要勾選“在單一檔案中儲存裝配體的所有連桿”。
小技巧:STL格式是一種三維圖形格式,被很多三維建模軟體支援(Mathematica也支援,所以我們要儲存為這個格式)。STL格式只儲存三維圖形的表面資訊,而且是用很多的三角形對圖形進行近似的表示。如果你的機器人外形比較簡單(規則的幾何體),那麼得到的STL檔案大小一般只有幾十KB ;可是如果外形很複雜(比如包含很多的孔洞、曲面),生成的STL檔案會很大(幾MB∼幾十MB)。對於一般配置的計算機,模型檔案超過100KB用Mathematica處理起來就比較慢了。為了讓模擬顯示地更流暢,可以利用免費軟體MeshLab對其進行化簡,MeshLab通常能夠在基本不改變外形的前提下將檔案大小縮減為原來的十分之一甚至更多。
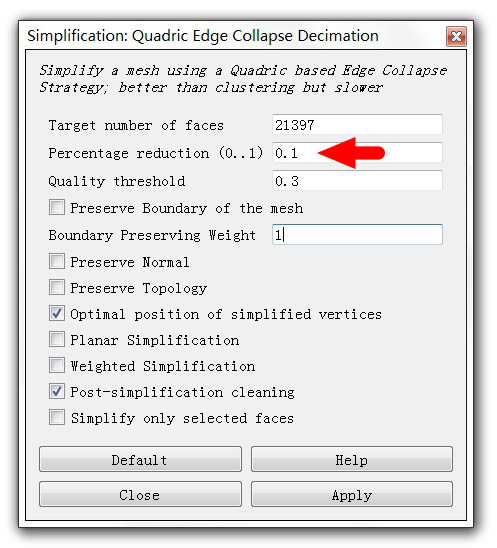
MeshLab的安裝和操作都是傻瓜式的,開啟後進入如下圖左所示的選單中,出現右圖的頁面,這裡的“Percentage reduction”表示縮減的百分比(1 表示不縮減,0.1 則表示縮減為原來的10%),設定好後點擊Apply並儲存即可。
然後在 Mathematica中匯入 STL 檔案,使用的程式碼如下(假設這些 STL 檔案儲存在 D:\MOTOMAN 資料夾下):
SetDirectory["D:\\MOTOMAN"]; (*設定檔案存放的地址,注意次級路徑用雙斜槓*)
n = 6; (*n是機械臂的自由度,文章後面還會用到*)
partsName = {"1.stl", "2.stl", "3.stl", "4.stl", "5.stl", "6.stl", "7.stl", "8.stl", "9.stl"}; (*分別是組成機械臂的9個連桿*)
robotPartsGraphics = Import[#, "Graphics3D"] & /@ partsName; (*一次性匯入所有連桿,並且匯入為可以直接顯示的圖形格式*)
robotParts = robotPartsGraphics[[;; , 1]]; (*從三維圖形中提取出幾何資料:頂點的三維座標和邊*)這裡我偷了個懶,為了少打些字,我把匯出連桿的檔名改成了從1到9的數字(這個機械臂的裝配體一共包含9個零件)。我們把匯入的模型顯示出來,效果如下圖。使用的程式碼如下:
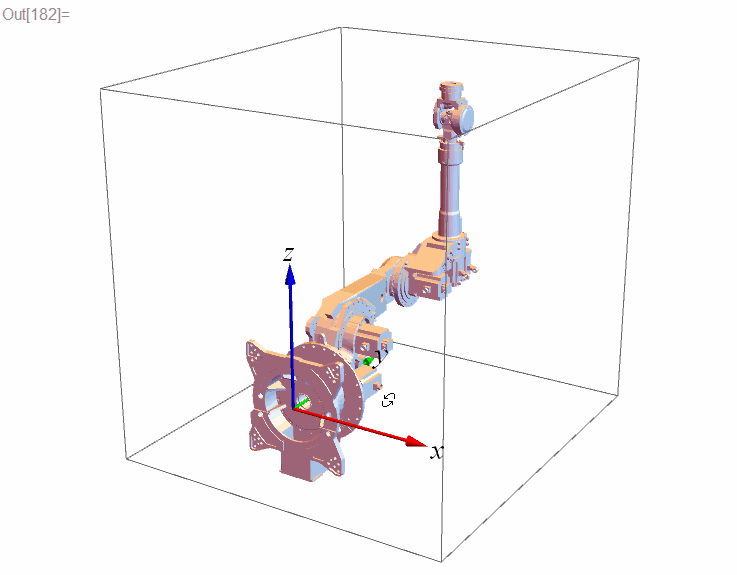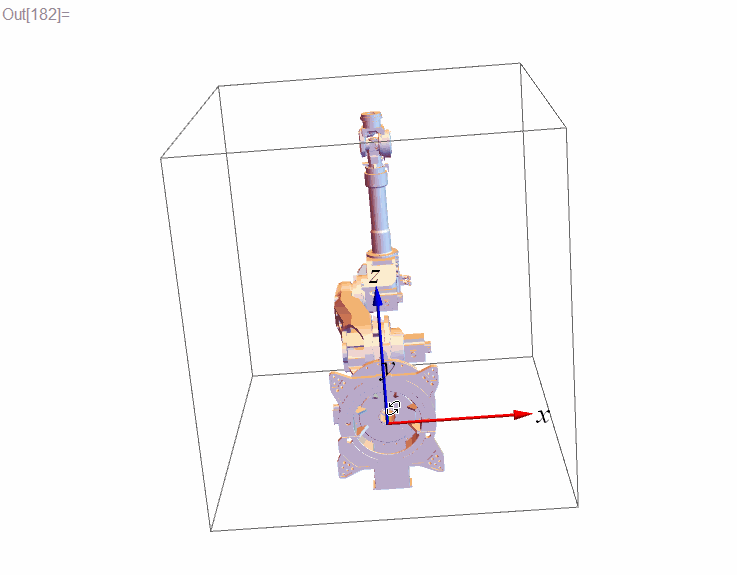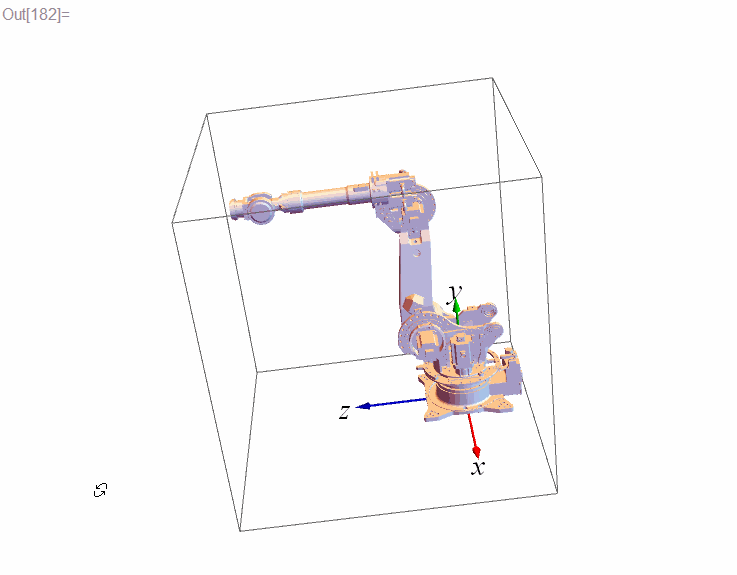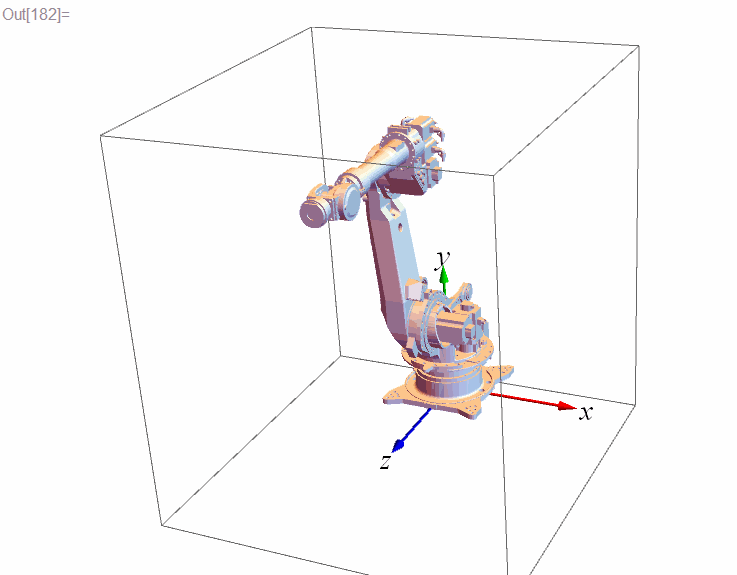
Graphics3D[{frame3D, robotParts}]說明:frame3D是三維座標系的三個正交的軸(軸的顏色分別是)。在機器人領域會用到大量的座標系及其變換,直接看數字總是不直觀,不如將座標系顯示出來更方便。定義 frame3D 的程式碼如下,這個座標系預設原點的位置在,以後我們稱這個座標系為“全域性座標系”。
frame3D = {RGBColor[#], Arrowheads[0.05], Arrow[Tube[{{0, 0, 0}, #}, 0.01]]} & /@ IdentityMatrix[3];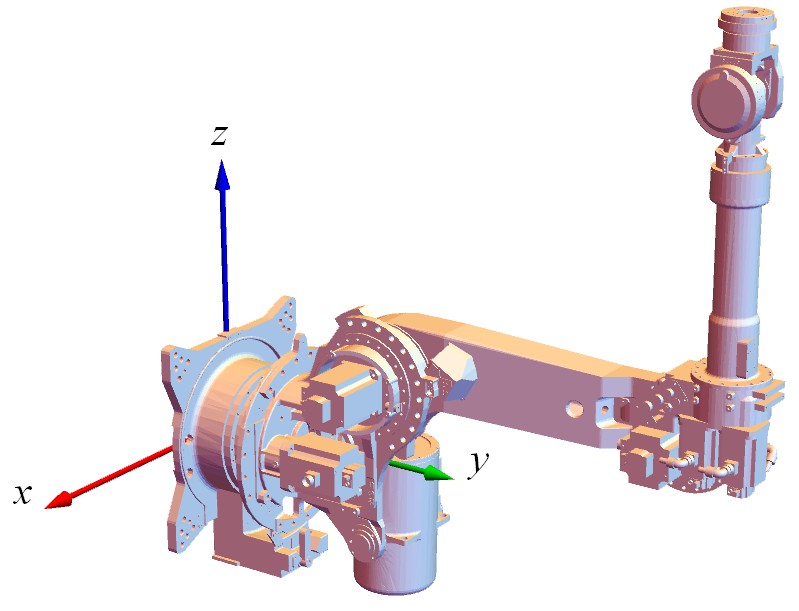
你可能會好奇:匯入的零件資料是以什麼樣的格式儲存的呢?
用來儲存機器人外形資料的
robotParts變數包含9個零件的資料,假如你想看第一個零件(對應的是基座,它通常用來將機械臂固定在大地上),可以輸入:
robotParts[[1]] (*雙層方括號中的數字表示對應第幾個零件*) 執行後的輸出結果是一堆由 GraphicsComplex 函式包裹著的數字,主要可分為兩部分:第一部分是零件幾何體所有頂點的三維座標;第二部分是組成零件幾何體的三角形(注意:構成每個三角形的三個頂點是第一部分點的序號,而不是座標值)。我們可以用以下程式碼將其分別顯示出來:
pts = robotParts[[1]][[1]]; (*零件1的第一部分:頂點的三維座標資料*)
triangles = robotParts[[1]][[2]]; (*零件1的第二部分:三角形面片*)
trianglesBlue = triangles /. {EdgeForm[] -> EdgeForm[Blue]}; (*三角形的邊顯示為藍色*)
Graphics3D[{GraphicsComplex[pts, trianglesBlue], Red, Point[pts]}]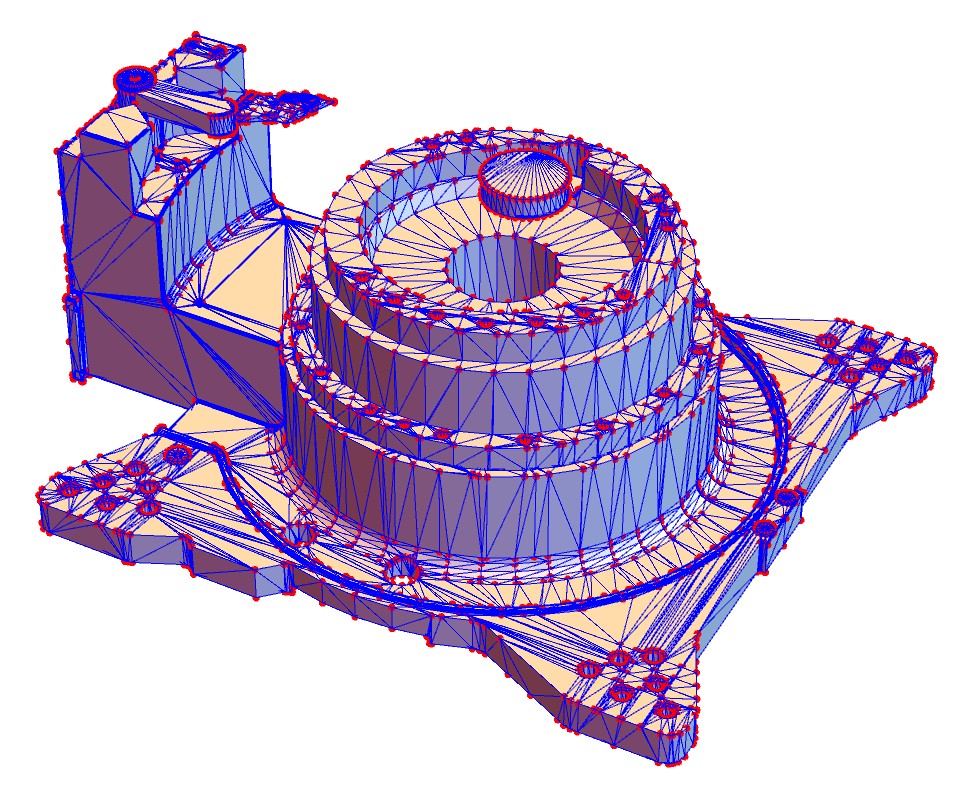
當然你可以任性而為,用哪個都可以。不過根據國家標準《GBT 16977-2005 工業機器人 座標系和運動命名原則》,機械臂基座座標系的 軸應該垂直於基座安裝面(一般是水平地面)、指向為重力加速度的反方向(也就是垂直地面向上), 軸指向機器人工作空間中心點的方向。制定國家標準的都是些經驗豐富的專家老手,我們最好跟國標保持一致(國標的作圖水平就不能提高點嗎?這圖怎麼感覺像小學生畫的)。

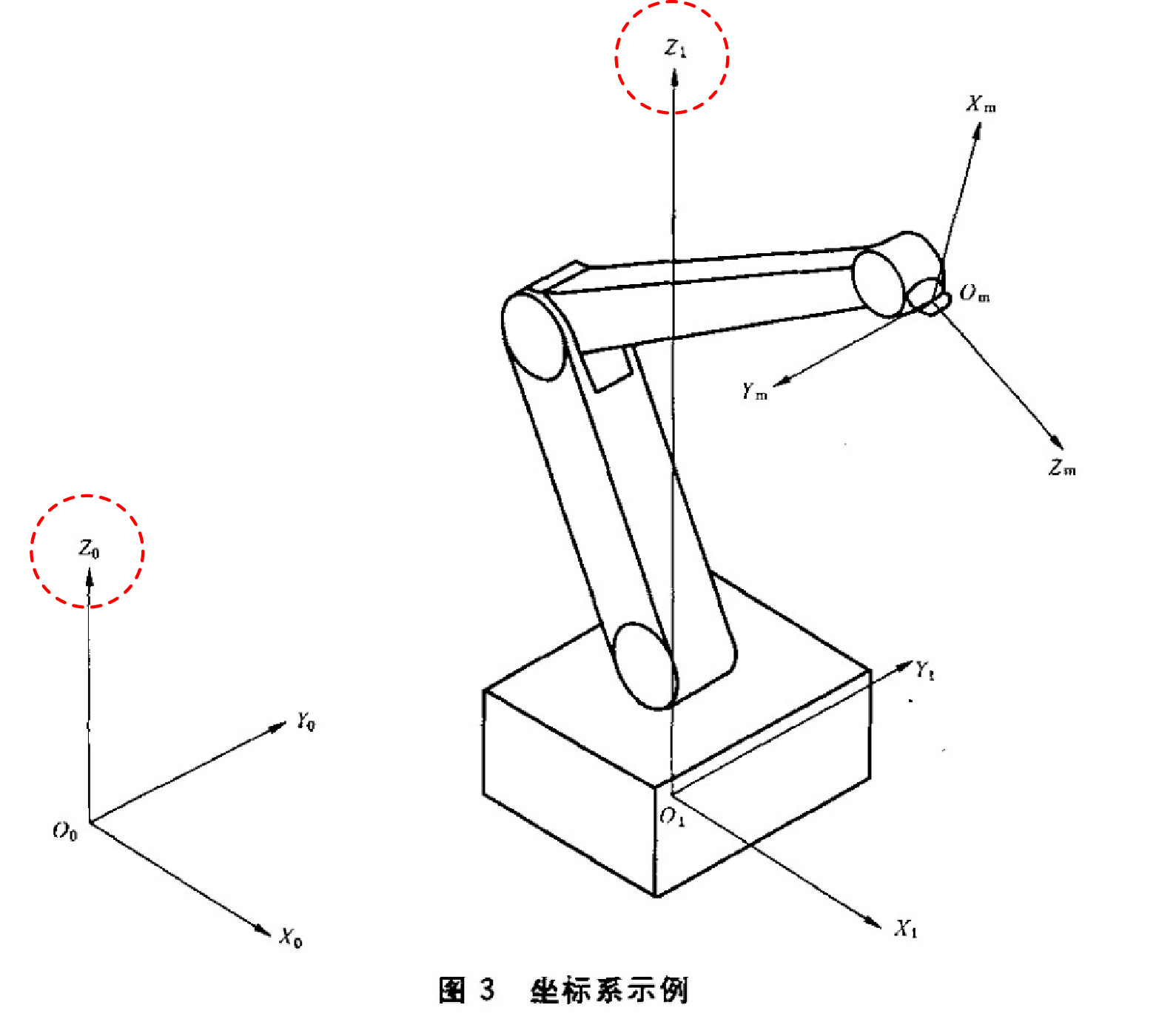
為此,我們定義旋轉矩陣(兩種定義效果一樣):
{Xaxis,Yaxis,Zaxis}=IdentityMatrix[3]; (*定義三個旋轉軸*)
rot = RotationMatrix[90 Degree, Zaxis].RotationMatrix[90 Degree, Xaxis]; (*注意第二次變換是在左邊乘*)
rot = RotationMatrix[90 Degree, Xaxis].RotationMatrix[90 Degree, Yaxis]; (*注意第二次變換是在右邊乘*) 然後用rot矩陣旋轉每個連桿(的座標,即儲存在第一部分robotParts[[i, 1]]中的資料):
robotParts=Table[GraphicsComplex[rot.# & /@ robotParts[[i, 1]], robotParts[[i, 2]]], {i, 9}];經過姿態變換後的機器人看起來舒服點了,只是有些蒼白。為了給它點個性(也方便區分不同的零件或者稱為連桿),我們給連桿設定一下顏色,程式碼如下。你可能注意到了,這裡我沒有使用迴圈去為9個連桿一個一個地設定顏色,而是把同類的元素(顏色)寫在一起,然後再和連桿列表一起轉置即可把顏色“分配”給各個連桿。這樣做的好處就是程式碼比較簡潔、清晰,以後我們會經常這麼做。
colors = {Gray, Cyan, Orange, Yellow, Gray, Green, Magenta, LightGreen, Pink}; (*1~9 各連桿的顏色*)
robotPartsColored = Transpose[{colors, robotParts}]; (*把顏色分配給各連桿*)
Graphics3D[robotPartsColored]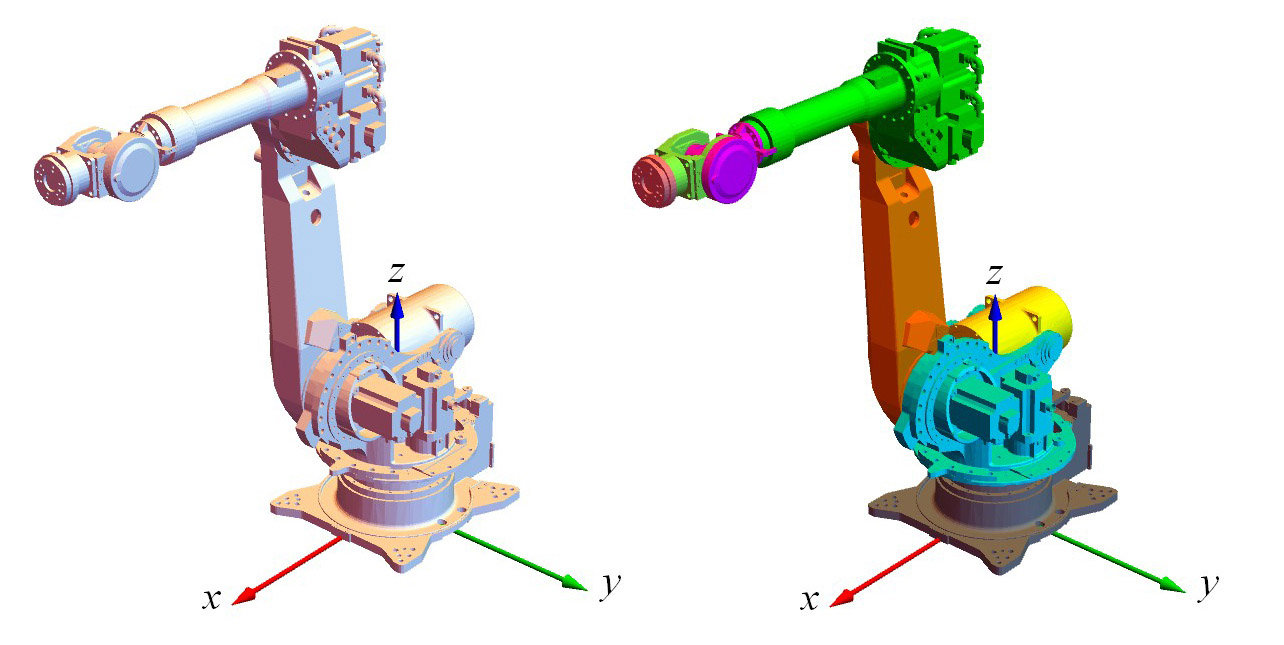
說明:現在的機器人姿勢(大臂豎直、小臂前伸)是6自由度機械臂的“零位”狀態,我們將此時機械臂各關節的角度認為是0。一般機械臂上都有各關節的零點位置標記,用於指示各關節的零點。我們用控制器控制機械臂時,發出的角度指令都是相對於這個零點位置的。零點位置不是必須遵守的,你可以將任意的角度設定為零位,不過為了統一,最好用機械臂固有的零位——也就是當前姿勢下各關節的角度。
3. 運動學模擬
前面的工作只是讓機械臂的模型顯示出來。如果想讓它動起來,那就要考慮運動學了。機器人這個學科聽起來高大上,可實際上現在大多數工業機器人的控制方式還是比較低階的,它們只用到了運動學,高階一點的動力學很少用,更不要提智慧了(它們要說自己有智慧,我們家的洗衣機和電視機都要笑掉大牙了)。看來要使用機器人,運動學是必不可少的,所以我們先來實現運動學。
在建立運動學模型之前我們需要了解機器人的機械結構。前面提到,MOTOMAN-ES165D 是一個6自由度的串聯機械臂。而6個自由度的機器人至少由7個連桿組成(其中要有一個連桿與大地固定,也就是基座)。可是我們匯入的連桿有9個,多出來的2個連桿是彈簧缸(基座上黃色的圓筒)的組成部分。MOTOMAN-ES165D 機器人能夠抓持的最大負載是165公斤,彈簧缸的作用就是作為配重平衡掉一部分負載的重量,要不然前端的關節電機會有很大的負擔。可是彈簧缸給我們的建模造成了麻煩,因為它導致“樹形拓撲”以及存在“閉鏈”,這不太好處理。為此,我們先忽略掉彈簧缸。
3.1 連桿的區域性座標系
機器人的運動也就是其構成連桿的運動。為了表示連桿的運動,我們要描述每個連桿的位置和姿態(合稱為“位姿”)。通常的做法是在每個連桿上固定一個座標系(它跟隨連桿一起運動),這個座標系被稱為“區域性座標系”。通過描述區域性座標系的位姿我們就可以描述每個連桿的位姿。如何選擇區域性座標系呢?理論上你可以任意選擇,不過區域性座標系影響後續程式設計和計算的難易程度,所以我們在選擇時最好慎重。在運動學建模和動力學建模中,座標系的選擇通常是不同的:
● 運動學建模時,連桿的區域性座標系一般放置在關節處,這是因為常用的 D-H 引數是根據相鄰關節軸定義的;
● 動力學建模時,連桿的區域性座標系一般放置在質心處,這是因為牛頓方程是關於質心建立的,而且關於質心的轉動慣量是常數,這方便了計算。
我們先考慮運動學,因此將區域性座標系設定在關節處。在SolidWorks中開啟任何一個連桿,都能看到它自己有一個座標系。描述一個連桿的每一條邊、每一個孔的座標都以這個座標系為參考,我們稱它為“繪圖座標系”。繪圖座標系通常不在質心處,因為在你還沒畫完連桿之前你根本不知道它的質心在哪裡。繪圖座標系通常在連桿的對稱中心或者關節處,我們不妨將每個連桿的繪圖座標系當做它的區域性座標系。
那麼下一個問題是每個連桿的繪圖座標系在哪兒呢?我們以第三個連桿為例說明,如下圖左所示,點選SolidWorks左側的“原點”標籤,圖中就會顯示繪圖座標系的原點。(如果你想將繪圖座標系顯示出來,可以先選中“原點”標籤,然後點選上方選單欄中的“參考幾何體”,再選擇“座標系”,然後直接回車即可看到新建的繪圖座標系,如右圖,可見它位於上面的關節軸)
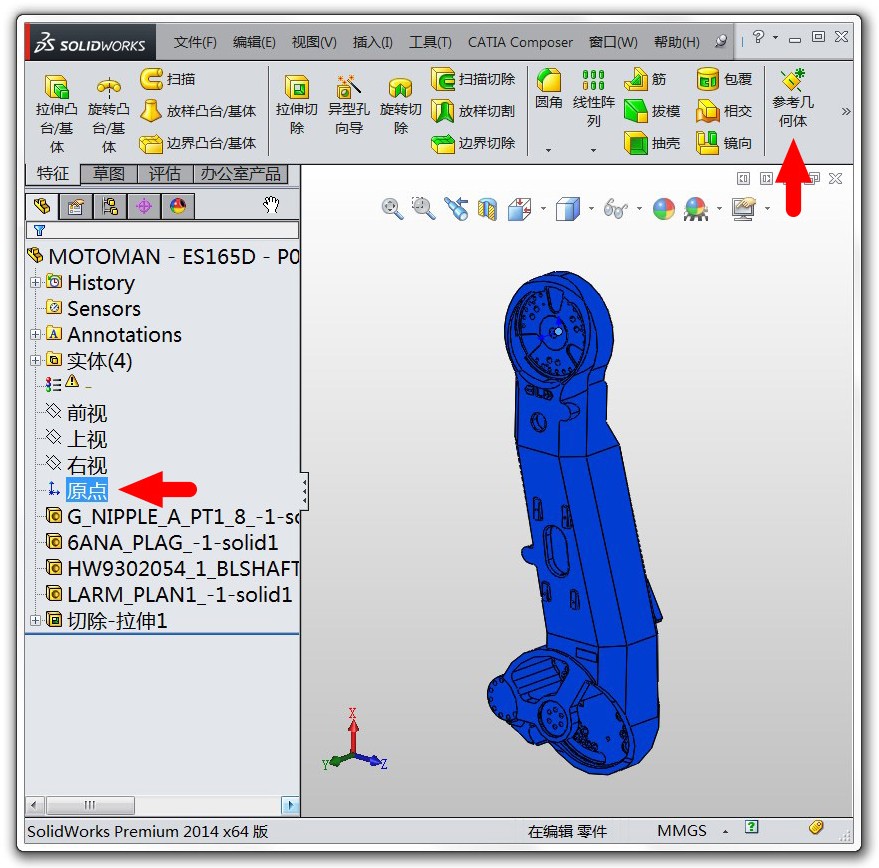
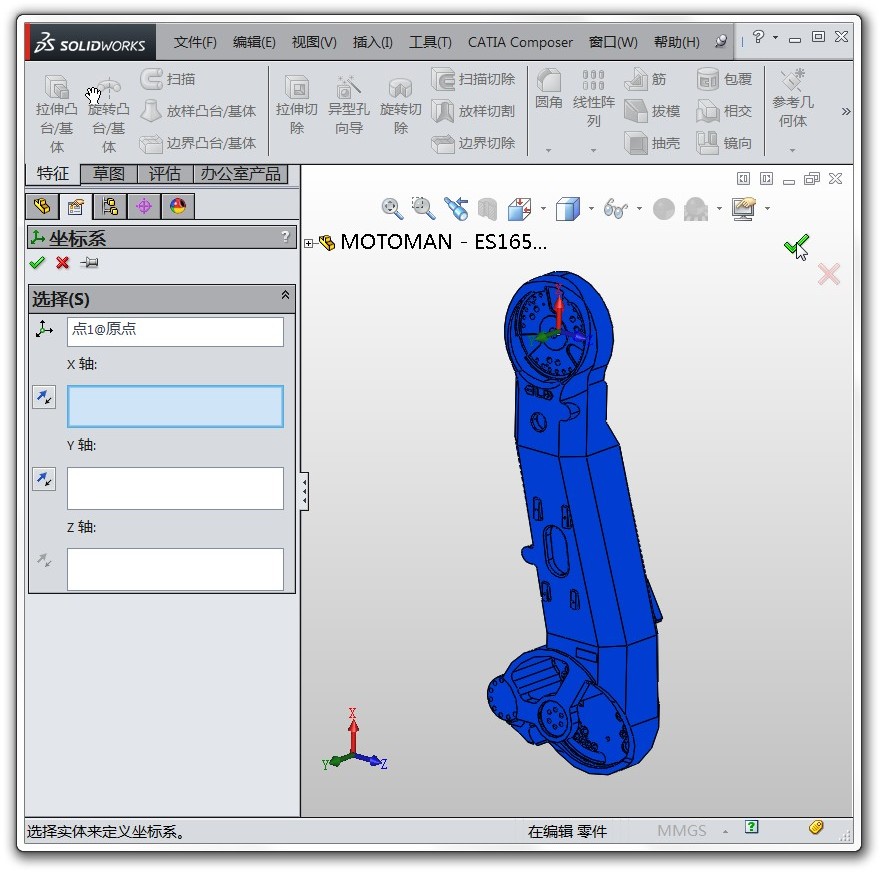
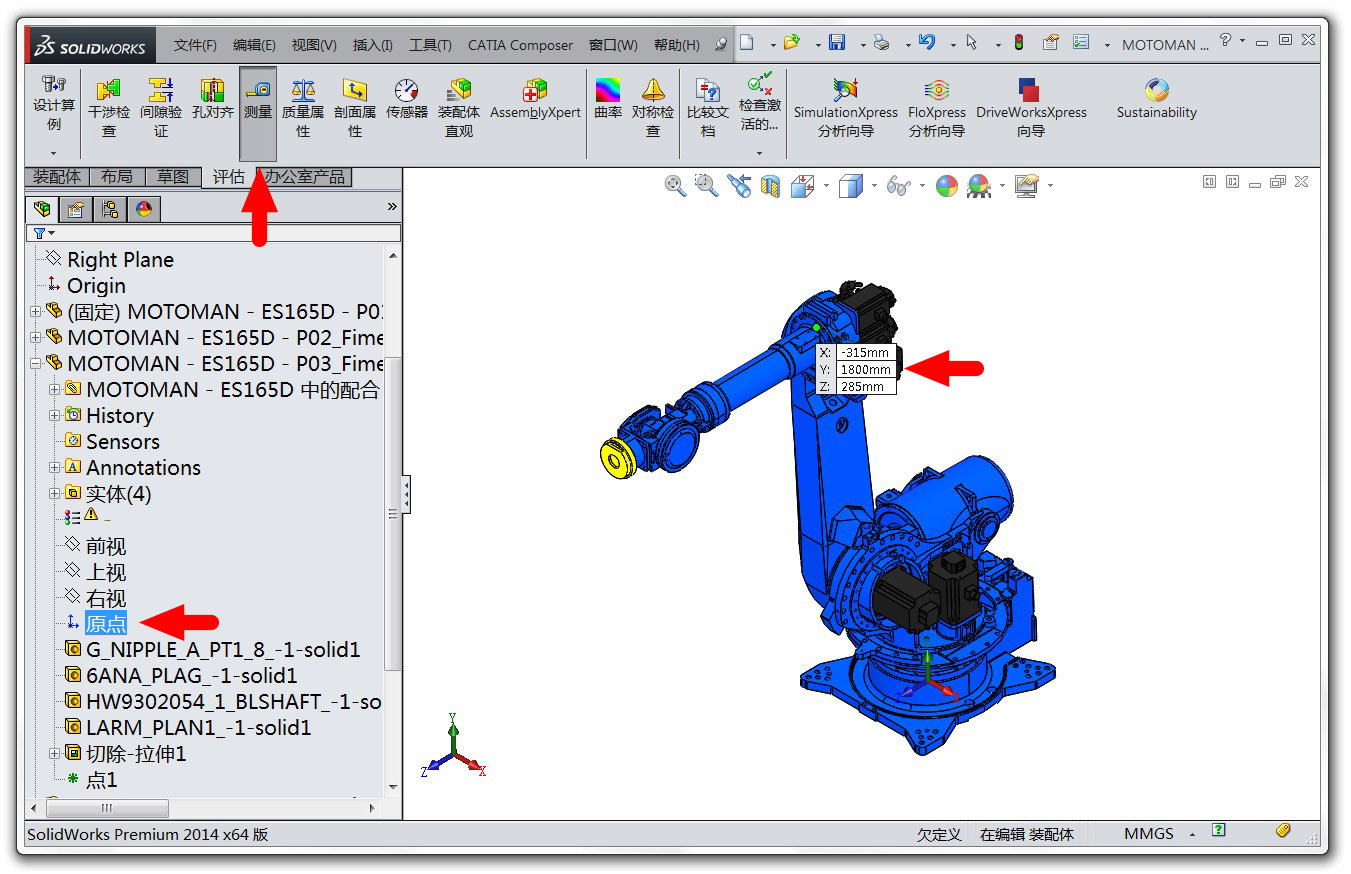
drawInGlobalSW = {{0, 0, 0}, {0, 650, 0}, {-315, 1800, 285}, {-53.7, 1800, 285}, {0, 2050, 1510}, {0, 2050, 1510}, {0, 2050, 1720.5}}/1000; 因為我們是在 SolidWorks 中測量的位置,所以這些位置值還是相對於 SolidWorks 的座標系( 軸朝上),要變到 軸朝上,方法仍然是乘以旋轉矩陣 rot:
drawInGlobal = Table[rot.i, {i, drawInGlobalSW}];以後我們會經常對點的座標進行各種各樣的變換(平移、旋轉),而且很多時候是用一個矩陣同時對很多個點的座標進行變換(例如上面的例子),不如定義一個運算元以簡化程式碼。我們可以定義運算元(其實是一個函式):
CircleDot[matrix_,vectors_]:=(matrix.#)&/@vectors; 所以前面的變換用我們自定義的運算元表示如下(複製到 Mathematica中後 \[CircleDot] 會變成一個Mathematica內部預留的圖形符號,這個符號沒有被佔用,所以這裡我徵用了):
drawInGlobal = rot\[CircleDot]drawInGlobalSW; (*哈哈!寫起來是不是簡單多了*)說明:本文出現的所有自定義的函式都給出了實現程式碼(Mathematica 自帶的函式首字母都是大寫。為了與官方函式區分,我自定義的函式一般採用小寫字母開頭,不過也有例外)。為了方便,我將這些自定義函式打包成一個函式包,每次執行程式時匯入此函式包即可使用裡面的函式。注意該函式包依賴另一個函式包 Screws.m (為了寫起來省事,我修改了其中部分函式的名字,為此重新定義了 myScrews.m)。在程式中匯入函式包的程式碼如下(如果函式包位於你的程式筆記本檔案的同一目錄下):
SetDirectory[NotebookDirectory[]]
<< myFunction.m你還記得嗎?最開始我們匯入機器人模型時,各連桿的位置都已經按照裝配關係確定好了,所以它們的座標也是相對於全域性座標系描述的。可是現在我們要讓機械臂動起來(並且顯示出來),這就需要移動這些座標。為了方便起見,最好能將每個連桿的座標表示在自己的繪圖座標系中,因為這樣我們只需要移動繪圖座標系就行了,而各點的座標相對它們所屬的繪圖座標系是不動的。應該怎麼做呢?很簡單,將連桿的座標減去繪圖座標系的原點在全域性座標系中的座標即可:
partsName = {"1.stl", "2.stl", "3.stl", "6.stl", "7.stl", "8.stl", "9.stl"}; (*已經去除了組成彈簧缸的2個零件:4號和5號*)
robotPartsGraphics = Import[#, "Graphics3D"] & /@ partsName;
robotParts = robotPartsGraphics[[;; , 1]];
robotParts = Table[GraphicsComplex[rot\[CircleDot]robotParts[[i, 1]], robotParts[[i, 2]]], {i, 7}];
robotParts = Table[GraphicsComplex[(# - drawInGlobal[[i]]) & /@ robotParts[[i, 1]], robotParts[[i, 2]]], {i, 7}];
colors = {Gray, Cyan, Orange, Green, Magenta, Yellow, Pink}; (*重新定義連桿的顏色*)
robotPartsColored = [email protected]{colors, robotParts}; 座標移動後的連桿如下圖所示(圖中的座標系是各個連桿自己的繪圖座標系,我沒有對座標轉動,所以繪圖座標系和全域性座標系的姿態相同)。我們一開始從 SolidWorks 匯出檔案時是一次性地匯出整個裝配體的。其實,如果我們挨個開啟各個連桿並且一個一個的匯出這些連桿,那麼得到資料就是相對於各自的繪圖座標系的,只不過這樣稍微麻煩一點。
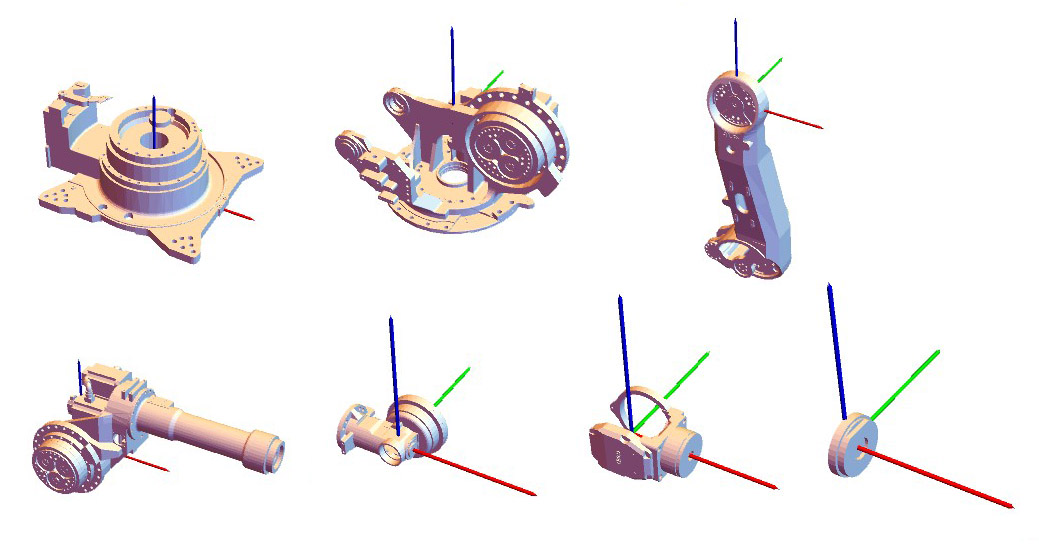
3.2 利用旋量建立運動學模型
下面我們討論如何建立運動學模型。描述機器人連桿之間幾何關係的經典方法是採用 D-H 引數(Denavit - Hartenberg parameters)。D-H 引數巧妙在