題目中針對的0，對於浮點型別，具體指的是0.0，自然對於指標型別就是NULL，對於整型就是0，一些常見筆試面試題中常出現，不要較真，十分歡迎提出改進意見。

本文很大程度上收到林銳博士一些文章的啟發，lz也是在大學期間讀過，感覺收益良多，但是當時林銳也是說了結論，lz也只是知其然，而不知其所以然，為什麼要那樣寫？為什麼要這樣用？往往一深究起來就稀裡糊塗了，現在有幸還是繼續讀書，我發現了很多問題理解的還不透徹，亡羊補牢。

比如：有int d;  int *d; bool d; double d；幾個變數，經過一系列的計算之後，那麼去判斷這個四個變數是否等於0該怎麼做？

很多菜鳥或者程式設計功底不紮實的就會出錯，一些爛書，尤其國內的一部分大學教材，教授程式語言的書籍，比如譚xx的，都存在很多不規範的誤導，甚至是錯誤，這樣的地方簡直太多了，並不是程式出了想要的正確結果，就算完事兒了。

一些類似我這樣的讀過幾本經典書籍，看過一些經典技術手冊，碼過若干行的程式碼等等，就會說這還不簡單，會類似的寫出：

 1     void isZero(double d)
 2     {
 3         if (d >= -DBL_EPSILON && d <= DBL_EPSILON)
 4         {
 5             //d是0處理
 6         }
 7     }
 8 
 9     void isZero(int d)
10     {
11         if (0 == d)
12         {
13             //
 
d是0處理
14         }
15     }
16 
17     void isZero(int *d)
18     {
19         if (NULL == d)
20         {
21             //d是空指標處理
22         }
23     }
24 
25     void isZero(bool d)
26     {
27         if (!d)
28         {
29             //d就認為是false 也就是0
30         }
31     }

沒錯，很多經典的教科書或者指南，一些技術類的講義，都會這樣教授。但是為什麼要這樣寫？

可能一部分人就糊塗了，不知道咋回答，搞技術或者做學問不是詩詞歌賦，結論經不起嚴謹的推敲就不能服眾，不可以說，書上是這樣寫的，或者老師告訴我的，那樣太low了。尤其是浮點數比較的問題，不只是0，類似的和其他的浮點數比較大小的問題也是一樣的。

要解決這個疑惑，必須先理解計算機是如何表示和儲存浮點資料的，期間參考了IEEE單雙精度的規範文件，和MSDN的一些文件，以及《深入理解計算機作業系統》一書。

1、先看看雙精度的伊布西龍（高等數學或者初等數學裡的數學符號就是它，epsilon）的值是多少

printf("%.40lf", DBL_EPSILON);

摺合為科學計數法：

2、再看一些例子

    printf("%0.100f\n", 2.7);
    printf("%0.100f\n", 0.2);

 printf("%0.100f\n", sin(3.141592653589793 / 6));

這個計算結果不是0.5，而是：

printf("%0.100f\n", 0.0000001);

列印結果是：

這樣的結果在不同機器或者編譯器下，有可能不同，但是能說明一個問題，浮點數的比較，不能簡單的使用==，而科學的做法是依靠EPISILON，這個比較小的正數（英文單詞episilon的中文解釋）。

EPSILON被規定為是最小誤差，換句話說就是使得EPSILON+1.0不等於1.0的最小的正數，也就是如果正數d小於EPISILON，那麼d和1.0相加，計算機就認為還是等於1.0，這個EPISILON是變和不變的臨界值。

官方解釋：

For EPSILON, you can use the constants FLT_EPSILON, which is defined for float as 1.192092896e-07F, or DBL_EPSILON, which is defined for double as 2.2204460492503131e-016. You need to include float.h for these constants. These constants are defined as the smallest positive number x, such that x+1.0 is not equal to 1.0. Because this is a very small number, you should employ user-defined tolerance for calculations involving very large numbers.

一般可以這樣寫，防止出錯：

 1     double dd = sin(3.141592653589793 / 6);
 2     /*if (dd == 0.5)
 3     {取決於不同的編譯器或者機器平臺……這樣寫，即使有時候是對的，但是就怕習慣，很容易出錯。
 4     }*/
 5 
 6     if (fabs(dd - 0.5) < DBL_EPSILON)
 7     {
 8         //滿足這個條件，我們就認為dd和0.5相等，否則不等
 9         puts("ok");//列印了ok
10     }

為什麼浮點數的表示是不精確的？（簡單的分析，否則裡面的東西太多了）

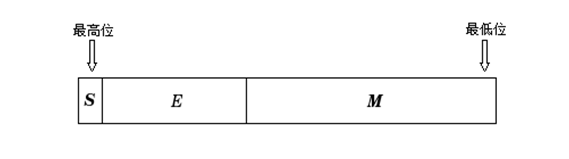
這得先說說IEEE（Institute of Electrical and Electronic Engineers ）754標準，此標準規定了標準浮點數的格式，目前，幾乎所有計算機都支援該標準，這大大改善了科學應用程式的可移植性。下面看看浮點數的表示格式：n是浮點數，s是符號位，m是尾數，e是階數，回憶高中的指數表示。

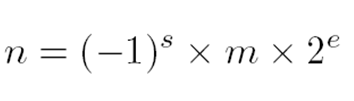
IEEE標準754規定了三種浮點數格式：單精度、雙精度、擴充套件精度。

前兩者正好對應C、C++的float、double，其中，單精度是32位，S是符號位，佔1位，E是階碼，佔8位，M是尾數，佔23位，雙精度是64位，其中S佔1位，E佔11位，M佔52位。拿intel架構下的32位機器說話，之前在計算機儲存的大小端模式解析說過處理器的兩類儲存方式，intel處理器是小端模式，為了簡單說明，以單精度的20000.4為例子。

20000.4轉換為單精度的2進位制是多少？

此單精度浮點數是正數，那麼尾數符號s=0，指數（階數）e是8位，30到23位，尾數m（科學計數法的小數部分）23位長，22位到0位，共32位，如圖

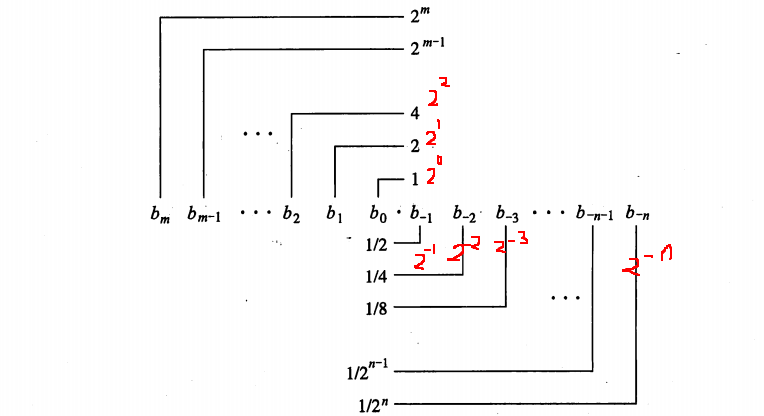
先看整數部分，20000先化為16進位制（4e20）16，則二進位制是（100 1110 0010 0000）2，一共15位。

再看小數部分，0.4化為二進位制數，這裡使用乘權值取整的計算方法，使用0.X迴圈乘2，每次取整數部分，但是我們發現，無論如何x2，都很難使得0.X為0.0，就相當於十進位制的無限迴圈小數0.33333……一樣，10進位制數，無法精確的表達三分之一。也就是人們說的所謂的浮點數精度問題。因單精度浮點數的尾數規定長23位，那現在乘下去，湊夠24位為止，即再續9位是（1.011001100）2

----------------------------------------------------------------------------------------------------------------

這裡解釋下為什麼是1. ……  且 尾數需要湊夠24位，而不是23位？

尾數M，單精度23位、雙精度52位，但只表示小數點之後的二進位制位數，也就是假定M為 “010110011...” ， 二進位制是 “ . 010110011...” 。而IEEE標準規定，小數點左邊還有一個隱含位，這個隱含位絕大多數情況下是1，當浮點數非常非常非常小的時候，比如小於 2^(-126) (單精度)的時候隱含位是0。這個尾數的隱含位等價於一位精度,於是M最後結果可能是"1.010110011...”或“0.010110011...”。也就是說尾數的這個隱含位佔了一位精度！且尾數的隱含位這一位並不存放在記憶體裡。

----------------------------------------------------------------------------------------------------------------

則20000.4表示為二進位制 = 100 1110 0010 0000 . 0110 0110 0

科學計數法為1.00 1110 0010 0000   0110 0110 0 x 2^14（此時尾數的隱含位是1，但是不放在記憶體）小數點左移了14位，單精度的階碼按IEEE標準長度是8位，可以表示範圍是-128 ~ 127，又因為指數可以為負的，為了便於表示和便於計算，那麼IEEE的754標準就人為的規定，指數都先加上1023（雙精度的階碼位數是11位，範圍是-1024~1023）或者加上127。

那麼單精度的浮點，階碼的十進位制就是14+127=141，141的二進位制=10001101，那麼階碼就是10001101，符號位是0，合併為32位就是：

0，10001101，00111000100000011001100

（1.00 1110 0010 0000   0110 0110 0尾數的小數點左邊的1不存入記憶體）

簡單的看，縱觀整個過程，浮點數的表示在計算機裡經常是不精確的！除非是0. ……5的情形。

因為乘不盡，且IEEE754標準規定了精度，實數由一個整數或定點數（即尾數）乘以某個基數（計算機中通常是2）的整數冪得到，這種表示方法類似於基數為10的科學記數法。

所以浮點數運算通常伴隨著因為無法精確表示而進行的近似或舍入。但是這種設計的好處是可以在固定的長度上儲存更大範圍的數。

總之就是一句話：浮點數無法精確的表示所有二進位制小數。好比：用10進位制數不能精確表示某些三進位制小數0.1(3)=0.33333333333……(10)，同理，用二進位制小數也不能精確表示某些10進位制小數。

有一個問題，為什麼8位二進位制的表達範圍是-128到127？

必須知道：計算機裡的一切數都是用補碼來表示！大部分補碼反碼原碼相關的知識在《計算機組成原理》課程都有講授

我只說書上沒有的，思考和複習了下，大概是這樣的：

二進位制直接表達0，有正0和負0的情況，比如原碼的0000 0000和1000 0000。且計算機進行原碼減法比較不爽。因為計算機裡進位容易，借位比較複雜！具體怎麼不爽這裡不再考證。

那麼最後人們決定使用補碼來表達計算機裡的一切數，這裡不得不提一個概念——模：一個系統的計量範圍，比如時鐘的計量範圍是12、 8位二進位制數的計量範圍是2^8.

對時鐘：從中午12點調到下午3點，有兩種方法，往前撥9個小時，或者往後撥3個小時，9+3=12，同理在計算機使用補碼就是這個道理，可以使用補碼代替原碼，把減法化為加法。方便運算加減，且補碼的0只有一種表達方式，比如四位元組的補碼（1000 0000 0000 0000 0000 0000 0000 0000），可以規定為-0，也可以看成0x8000 0001 - 1的結果，因為補碼沒有正負0，那麼人為規定是後者的含義！它就是四位元組負數的最小的數。那麼對一位元組，如下：

+127=0111 1111（原碼=反碼=補碼）

……

+1  = 0000 0001

0    = 0000 0000

……

-126= 1111 1110（原碼）= 1000 0001（反碼）=1000 0010（補碼）

-127= 1111 1111（原碼）= 1000 0000（反碼）=1000 0001（補碼），顯然，還差一個數，1000 0000（補碼），根據前面說的，它就是一位元組負數最小的數了！

就是原碼-128，針對補碼1000 0000求原碼，記住方法，和原碼求補碼是一樣的，都是符號位不變，取反加1，則1000 0000（補碼） = 1111 1111 + 1 = 1 1000 0000（原碼），精度多了一位，則捨棄，為1000 0000（原碼），和補碼一樣。

故取值範圍是1000 0000到0000 0000到0111 1111，-128到0到+127，其他位數同理，有公式曰：-2^(n-1)到+2^(n-1) - 1，其它可以套這個公式。

還有一個問題，浮點數用==比較怎麼了？完全可以執行！

這個問題，其實已經唄討論了很多年，浮點數的比較，千萬不能鑽牛角尖，“我就用==比較，完全能執行啊！”，我靠，沒人說這句程式碼是錯的好麼？

那麼到低是對還是錯的，關鍵還是看你想要什麼？！你想要的結果 和 你所做的東西反映的結果，是不是保持了一致？！明白了這個，就明白==該不該用。

其實個人認為，林銳博士 說的這是錯誤，感覺也不太準確，因為有鑽牛角尖的會想不通。

還有一個問題，逼逼了那麼多，浮點數無法精確表達實數，那為啥epsilon的大小是尼瑪那樣的？

1 #define DBL_EPSILON      2.2204460492503131E-16 
2 #define FLT_EPSILON     1.19209290E-07F 
3 #define LDBL_EPSILON     1.084202172485504E-19 

前面已經說了，數學上學的實數可以用數軸無窮盡的表示，但是計算機不行，在計算機中實數和浮點數還是不一樣的，我個人理解。浮點數是屬於有理數中某特定子集的數的數字表示，在計算機中用以近似表示任意某個實數。

在計算機中，整數和純小數使用定點數表示，叫定點小數和定點正數，對混合有正數和小數的數，使用浮點數表示，所謂浮點，浮點數依靠小數點的浮動（因為有指數的存在）來動態表示實數。靈活擴大實數表達範圍。但在計算過程中，難免丟失精度。

至於epsilon的大小，前面也貼出了官方定義，它就規定了，當x（假如x是雙精度）落在了+- DBL_EPSILON之內，x + 1.0 = 1.0，就是這麼規定的。x在此範圍之內的話，都唄計算機認為是0.0 。

浮點數表達的有效位數（也就是俗稱的精度）和表達範圍不是一個意思

經常說什麼單精度一般小數點精度是7-8位，雙精度是15-16位，到低怎麼來的呢？前面說了，單精度數尾數23位，加上預設的小數點前的1位1，2^(23+1) = 16777216。關鍵： 10^7 < 16777216 < 10^8，所以說單精度浮點數的有效位數是7-8位，這個7-8位說的是十進位制下的，而我們前面說的尾數位數那是二進位制下的，需要轉換。

又看，雙精度的尾數52位儲存，2^(52+1) = 9007199254740992，那麼有10^16 < 9007199254740992 < 10^17，所以雙精度的有效位數是16-17位。

貌似實際編碼中，大部分直接用double了，省的出錯。

關鍵是要巨集觀的理解為什麼不精確，具體怎麼算倒是次要。總之應付筆試面試足夠了。拋磚引玉，如有錯誤，歡迎指出。