最小生成樹演算法中Prim是通用的一種演算法。其大致的思想可以用通俗的語言去描述。首先看一段其他部落格中的專業描述：

“設圖G頂點集合為U，首先任意選擇圖G中的一點作為起始點a，將該點加入集合V，再從集合U-V中找到另一點b使得點b到V中任意一點的權值最小，此時將b點也加入集合V；以此類推，現在的集合V={a，b}，再從集合U-V中找到另一點c使得點c到V中任意一點的權值最小，此時將c點加入集合V，直至所有頂點全部被加入V，此時就構建出了一顆MST。因為有N個頂點，所以該MST就有N-1條邊，每一次向集合V中加入一個點，就意味著找到一條MST的邊”。

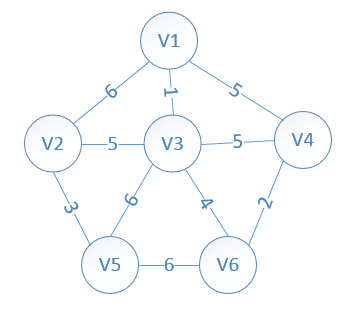
    Prim演算法的思想就是遍歷所有最小權值的邊，當然這種遍歷是在依次新增頂點的基礎上。通俗來講，以下圖為例，可以首先選擇V1為為起點，然後遍歷V = {v2,v3,v4,v5,v6}這其餘的5個頂點；遍歷完成後發現V3到V1的值最小，那麼將V3加入到已經遍歷的節點集合，暫時用W表示，則W={v1,v3}，V1開始時預設起始點，已經加入；此時V = {v2,v4,v5,v6},然後遍歷這幾個頂點到W中頂點的權值哪個最小，然後選擇哪個，下一個應該選擇V6；依次類推，這就是Prim基本的演算法思想，演算法複雜度當然為n*n；

以下是《大話資料結構》中的程式碼實現，同時加了自己的一些理解註釋

/*圖的鄰接矩陣定義*/
typedef char VertexType;
typedef int EdgeType;
#devine MAXVEX 100
#define INFINITY 65535
typedef struct
{
 VertexType vexs[MAXVEX];//頂點表
 EdgeType arc[MAXVEX][MAXVEX];//邊表。可以表示權值的大小
 int numVertexes,numEdges;//邊和頂點的最大個數
}MGraph;

void MiniSpanTree_Prim(MGraph G)
{
 int min,i,j,k;
 int adjvex[MAXVEX] ={0};//存放頂點的下標，可以看做一個存放已經被選中的頂點的集合
 int lowcost[MAXVEX] ={0};//存放邊的權值
 
 /*先選擇一個起始點，加入從0開始，我們的頂點採用自然數字0~MAXVEX*/
 adjvex[0] = 0;
 lowcost[0]=0;//初始化第一條邊為0，代表節點0已經加入了adjvex的集合
 for(j=0;j<G.numVertexes;j++)
 {
  lowcost[j]=arc[0][j];//將與第一個節點邊的權值存入到陣列
  adjvex[j] = 0;//全都初始化為0的下標
 }
 /*開始遍歷出去第一個節點的其他節點*/
 for(i=1;i<G.numVertexes;i++)
 {
  min = INFINITY;
  for(j=0;j<G.numVertexes;j++)
  {
   if(lowcost[j]!=0 && min>lowcost[j])
   {
    min = lowcost[j];
    k=j;//記錄下當前這個點的下標
   }
   j++;
  }//迴圈退出時，便找到了離當前節點最近距離的點
     printf("(%d,%d)"adjvex[k],k);
  lowcost[k]=0;//代表第j個節點已經被遍歷了。
  /*下邊這個迴圈是來尋找新加入的節點與其他頂點的最小值，然後存入lowcost陣列中，同時更新下標陣列*/
  if(j=1;j>G.numVertexes;j++)
  {
   if(lowcost[j]!=0; && G.arc[k][j] < lowcost[j])
   {
       lowcost[j] = G.arc[k][j];//將較小值存入到lowcost中
    adjvex[j] = k;//將k的下邊存入頂點陣列
   }
   
  }
 }
}