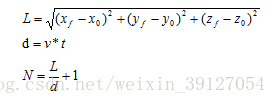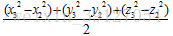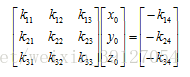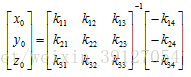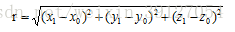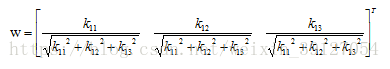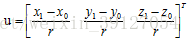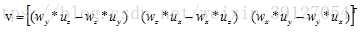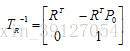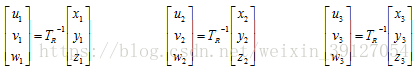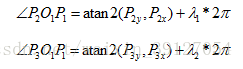1 引言

隨著6R機械人的使用性越來越廣，對機械人的軌跡規劃的要求也越來越高，機器人軌跡規劃是機器人執行作業任務的基礎。使用的軌跡規劃演算法，直接決定了機器人的運動軌跡、平滑程度，且使點位運動有足夠高的精度且滿足規劃路徑的約束條件。

本文將在對機器人完成建模以及運動學解算後的基礎上，對機器人進行笛卡爾空間軌跡規劃的研究，主要分為直線軌跡規劃與圓弧軌跡規劃。

2 任務位置規劃

  2.1直線軌跡規劃

插補可以分為定時插補和定距插補，定時插補是指每隔固定時間週期插補一個插補點，簡單易用，但是缺點是如果示教點過遠，即定時插補出來的兩個插補點距離較遠，精度降低，但可以通過多取示教點或插入中間點來解決。定距插補是指每隔固定距離就插補一個點，只要插補的距離足夠近，插補出來的曲線精度就越高，但是這個插補方法是恆定距離，對於不同速度就有不同的時間，難以實現，對演算法要求較高，所以一下的研究均採用定時插補。

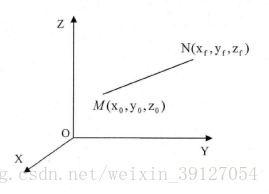
 圖1    笛卡爾座標系下兩點

笛卡爾空間直線規劃演算法是在已知直線的始末兩點的位置和姿態，求各軌跡插補點的位姿，大多數情況下機器人沿直線運動時其姿態不變，所以無姿態插補，而對於那些要求姿態改變的情況，就需要進行姿態插補。如圖1所示，已知直線始末兩點M，N相對於基座標系的座標姿態，當然這些已知的位置和姿態通常是可以通過示教方式直接得到的。假設v為要求的沿直線的速度，t為插補的時間間隔，我們可以求出直線長度L，t間隔內的距離d以及插補數N如下：

那麼相鄰插補點各軸增量與各軸插補點座標值如下：

相鄰插補點增量：                                                                插補點的座標： 

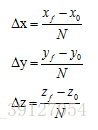
其中：i = 0,1,2…N

至此機器人的直線規劃已完成。

2.1圓弧軌跡規劃

三維空間中任意不共線的三點可以確定一個空間圓，空間圓和直線一樣，都是機器人空間作業軌跡的重要元素之一，在規劃其他較為複雜的軌跡時，都扮演著非常基礎卻很重要的角色。在笛卡爾空間圓弧的軌跡規劃中，為了計算方便，必須運用到座標系變換，也就是說要先在圓弧所在圓弧所在平面建立一個新的直角座標系，在這新的直角座標系中計算出圓弧的各插補點在新座標中的值，最後將所得的中間插補點再經過變換矩陣來轉變至用笛卡爾空間來描述。

三點確定一段圓弧，設機器人末端執行器從起始位置P1(x1,y1,z1)經過中間點P2(x2,y2,z2)最後到達終點P3(x3,y3,z3)，如果這三點不共線，就一定存在從起始點P1經中間點P2到終點P3的圓弧。現介紹圓弧軌跡規劃的演算法步驟：

（1）先求出圓心P0(X0,Y0,Z0)及其半徑

（2）以圓弧所在平面建立O1-UVW座標系，並求出該座標與基座標系的對映關係

（3）判斷圓弧軌跡，求出圓弧的總角度

（4）利用三角函式的關係，求出每個插補點的座標，並把它對映到基座標系

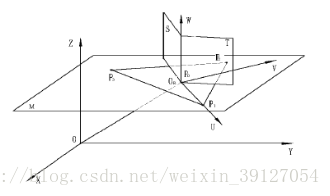
圖2    建立O1-UVW座標系

(1)進行第一個步驟：

已知空間中一平面方程的基本形式為：

K11x + k12y + k13z + k14 = 0

由P1 (x1,y1,z1)，P2(x2,y2,z2) 和P3(x3,y3,z3)三點確定一平面M，其平面方程可寫列出行列式：

將其展開：

[(y1 – y3)(z2 – z3) – (y2 – y3) (z1 – z3)] (x – x3) +

[(x2 – x3)(z1 – z3) – (x1 – x3) (z2 – z3)] (y – y3) +

[(x1 – x3)(y2 – y3) – (x2 – x3)(y1 – y3)] (z – z3) = 0

將上式化簡可得：

K11  =  (y1 – y3)(z2 – z3) – (y2 – y3) (z1 – z3)

K12  =  (x2 – x3)(z1 – z3) – (x1 – x3) (z2 – z3)

K13  =  (x1 – x3)(y2 – y3) – (x2 – x3)(y1 – y3)

K14  =  –(K11x3 + K12y3 + K13z3)

過P1，P2的中點且與P1 P2垂直的平面T的方程為：

K21x + k22y + k23z + k24 = 0     

式中：K21 = (x2 – x1)，K22 = (y2 – y1)，K23 = (z2 – z1)，K24 = 

過P2，P3的中點且與P2 P3垂直的平面S的方程為：

K31x + k32y + k33z + k34 = 0

式中：K31 = (x3 – x2)，K32 = (y3 – y2)，K33 = (z3 – z2)，K34 =

空間圓的圓心為平面M，T，S的交點。聯立三個平面方程，則可列出P1，P2，P3的外接圓的圓心座標P0 = [x0  y0  z0]的方程：

由此可求出圓心座標

進而可求出外接圓的半徑：

至此已完成第一個步驟

(2)  進行第二步驟：

建立圓弧所在平面O1—UVW的新座標系，進行座標系變換

以O1為原點建立新的座標系O1—UVW，O1W的方向與平面M的法向量方向一致。由於平面M的法向量的方向數分別為k11，k12，k13，則O1W軸在基座標系中的方向餘弦為：

令O1T軸的方向與O1 P1的向量方向一致，則O1T軸在基座標系中的方向餘弦為：

按右手法則，O1V軸在基座標系中的方向餘弦為O1W軸和O1U軸單位向量的叉乘方向，即v = w x u

利用新座標系O1—UVW的三個座標軸在基座標系中的方向餘弦u，v，w，即可建立基座標系O—XYZ到新座標系O1—UVW的變換矩陣TR為：

其逆矩陣TR-1可由齊次變換矩陣求逆得到，記：

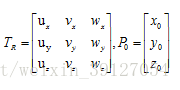
可以得到逆矩陣TR-1：

由此可見，基座標系下的空間圓，在新座標系O1—UVW下實質上是平面M上的平面圓，兩者關係可通過變換矩陣來相互轉換。至此兩個座標系的變換關係已求出。

（3）進行第三個步驟：

將P1，P2，P3，P0從基座標系中的值變換到O1—UVW新座標系中，設原來座標系中的值分別為P1 (x1,y1,z1)，P1(x2,y2,z2)，P1(x3,y3,z3)，P0(x0,y0,z0)新座標系中的值分別為(u1,v1,w1)，(u2,v2,w2)，(u3,v3,w3)，(u0,v0,w0)，則有下列求解式子：

由前面推導可知：u0 = v0 = w0 = w1 = w2 = w3 = 0，u1 = r

在新座標系上進行圓弧插補

①在對空間的圓弧軌跡規劃之前，現在座標系按照O1—UVW中作出平面M上的圓弧軌跡規劃，得到空間圓弧上各點在新座標系O1—UVW中的位置，然後利用座標變換，得到空間圓弧上這些點在基座標系中的位置，於是就完成了空間圓弧軌跡規劃。

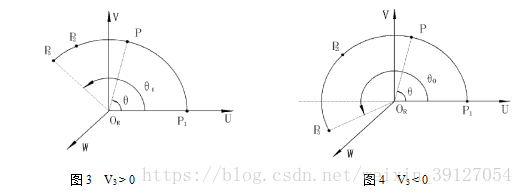
在把新座標系O1—UVW內的圓弧變換為基座標系的空間圓弧軌跡之前，需要確定圓弧的旋轉角度及方向，P1，P2，P3的順序確定圓弧的旋轉方向，在新座標系O1—UVW內確定O1P2，O1P3與U軸（即O1P1）之間的夾角大小：

在C#.NET程式語言中，內部數學函式Math.Atan2(y,x)弧度計算取值在-180~180度之間，所以上式中，當atan2(P2y , P2x) < 0時，λ1為1，否則取λ1為0，當atan2(P3y , P3x) < 0時，λ2為1，否則取λ2為0。比較∠P2O1P1與∠P3O1P1的大小，可以確定從P1依次運動到P2，P3的時候，圓弧運動的方向。當∠P2O1P1  <  ∠P3O1P1時，為逆時針方向運動，當∠P2O1P1  > ∠P3O1P1時，為順時針方向運動。

圖中的空間圓弧在座標系O1—UVW中的方向即為逆時針方向。逆時針方向時，圓弧對應的角度大小為θ=∠P3O1P1，順時針方向時，圓弧對應的角度大小為θ=2π-∠P3O1P1。

至此已求出規劃圓弧的總角度。

（4）進行第四個步驟：

通過以上的公式即可以得到空間圓弧在新座標系O1—UVW中的圓心位置，半徑大小，圓弧所對應的角度，以及運動的方向，接著在新座標系中將圓弧進行插值，計算各插補點。以P1為起始點，通過P2和P3點

的平面圓弧插值方程如下：（i表示第i個插補點,i = 1,2,3......）

  ，其中ui = r * cos(ωt * dir) , vi = r * sin(ωt * dir) , w = 0;

式中，dir為圓弧運動的方向係數，逆時針方向時dir = 1，順時針方向時dir = -1，ω為圓弧運動的角速度，t∈(0，tall)為運動時間，tall = θ /ω為總運動時間，總插補數（取整數）為。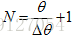

插補結果得到座標對映至基座標繫上。設點Pi在基座標系的座標值為(xi，yi，zi)，則有：

將新座標系O1—UVW中的位置插值量P通過上式的座標轉換關係轉變至基座標系中，把各插補點的位置和姿態通過運動學逆解，則可以得到各個插補點對應的關節角。

至此已完成了笛卡爾空間中的圓弧規劃。