AVL樹又稱作高度平衡二叉樹，它實際上是一種優化了的搜尋二叉樹。我們知道，由於二叉搜尋樹存在缺陷，有可能會退化成單鏈表，這樣的話搜尋的效率就降低了。為了將二叉搜尋樹的效率控制在O(logN)的級別，所以我們要給二叉搜尋樹加上一些條件，使得二叉搜尋樹高度平衡，時間複雜度為O(logN)。

性質：

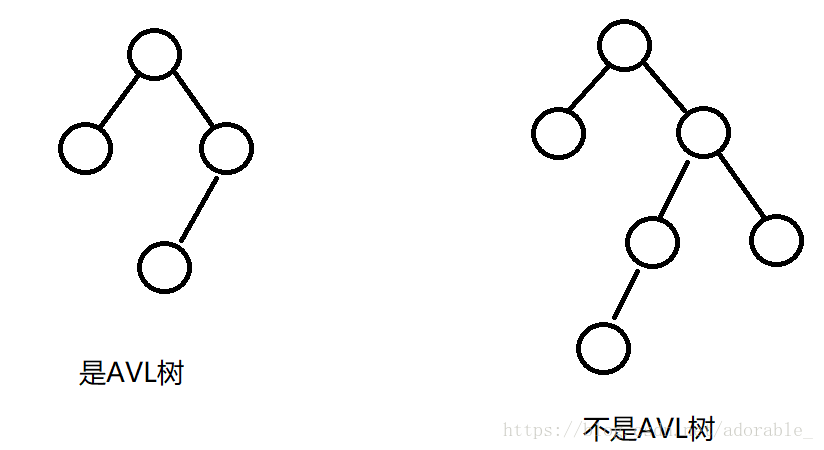
1. 左子樹和右子樹的高度之差的絕對值不超過1
2. 樹中的每個左子樹和右子樹都是AVL樹
3. 每個節點都有一個平衡因子(balancefactor–bf),任一節點的平衡因子是-1,0,1。(每個節點的平衡因子等於右子樹的高度減去左子樹的高度)

平衡旋轉：
  如果一棵樹原來是平衡的二叉搜尋樹，現在向裡面插入一個結點，造成了不平衡，這時候我們就要調整這棵樹的結構，使之重新平衡。首先我們來看看造成不平衡的結構都有哪幾種以及如何調整。

（1）由插入引起的平衡旋轉
平衡因子的更新原則：

1、右邊增加，父親bf++
2、 左邊增加，父親bf- -

• 父親bf == 0，結束更新，返回（子樹高度不變）
• 父親b f== -1或1，子樹高度變了，繼續往上更新
• 父親bf == 2或-2，子樹不再是AVL樹，需要旋轉，變平衡

注意：所有的插入都是建立在平衡二叉樹的基礎之上的。

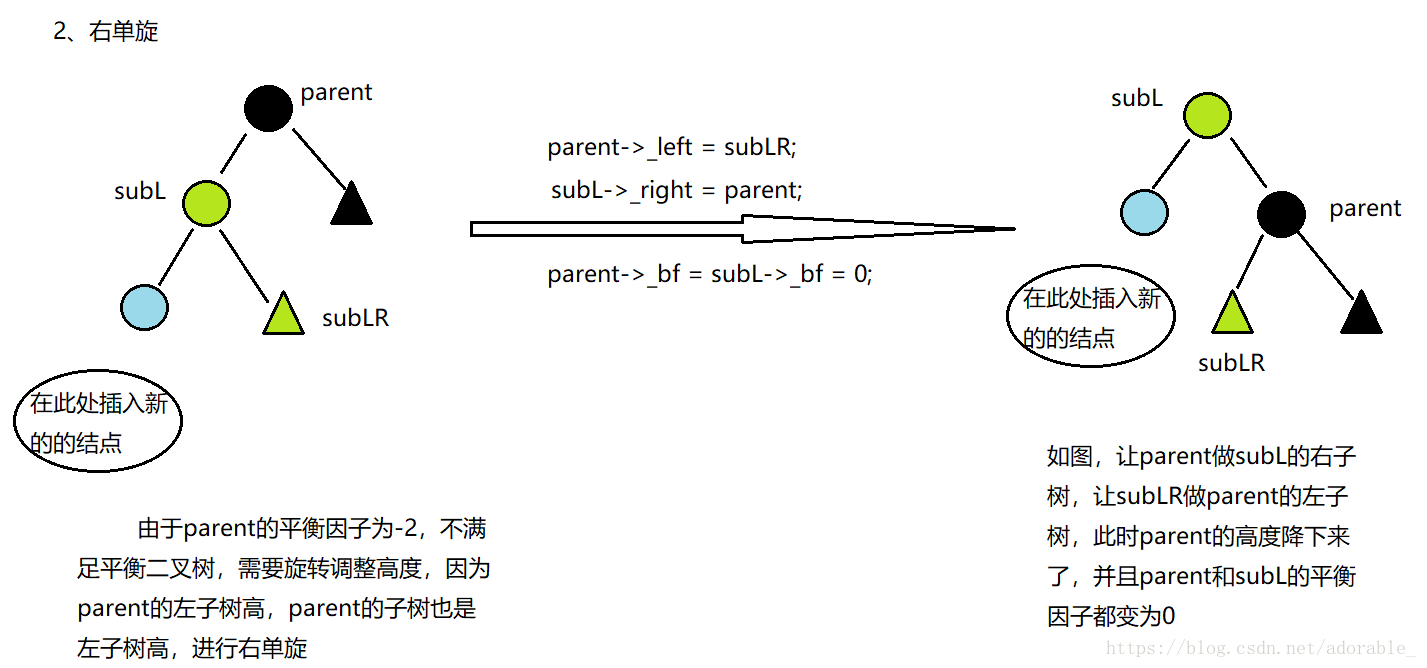
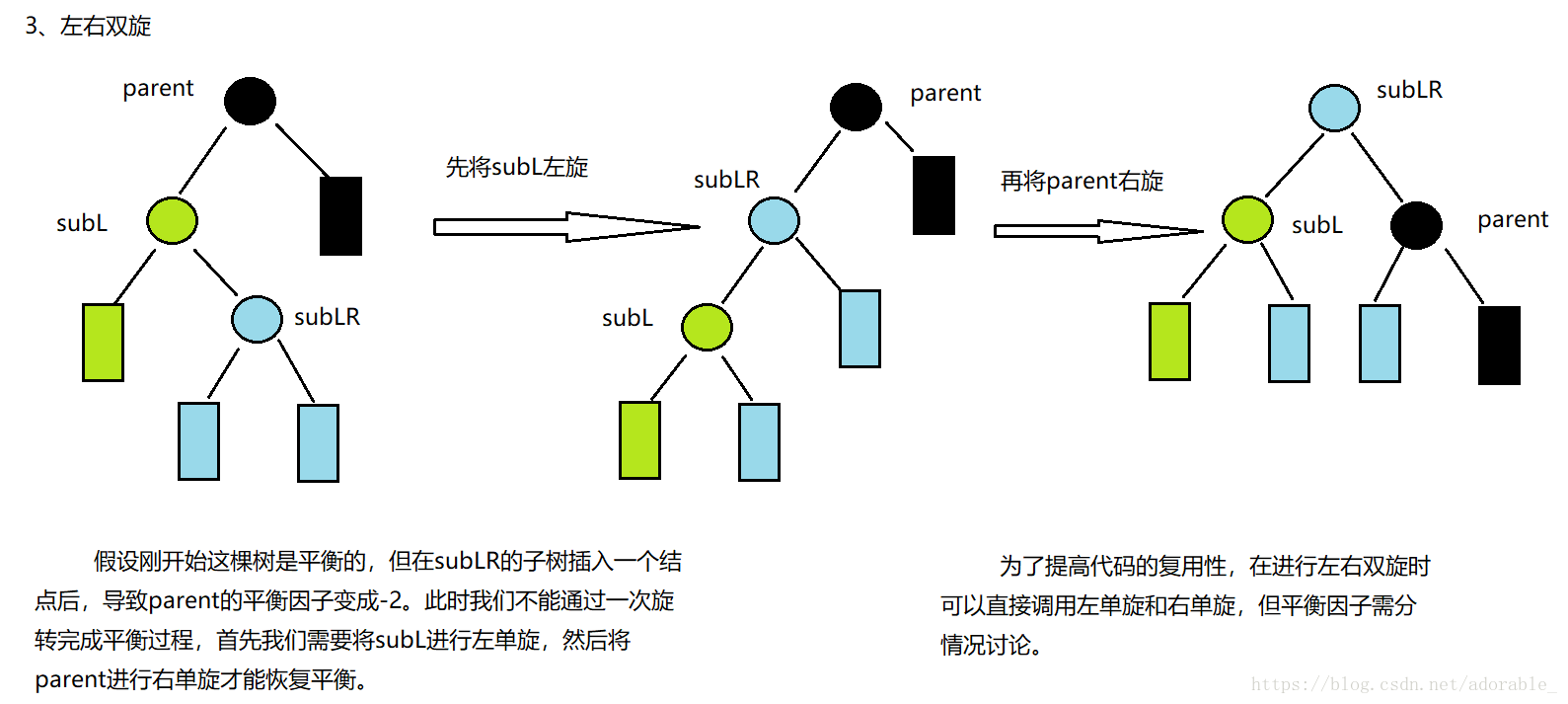
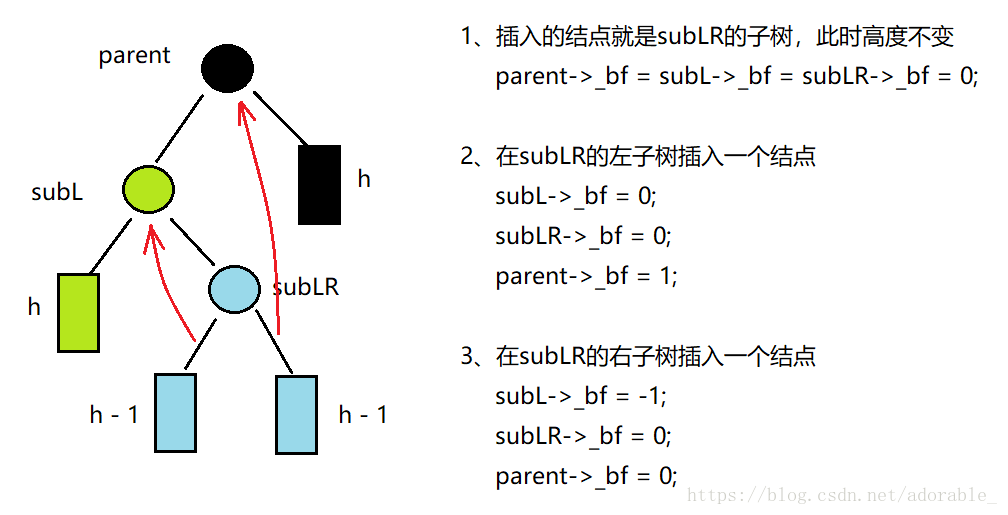
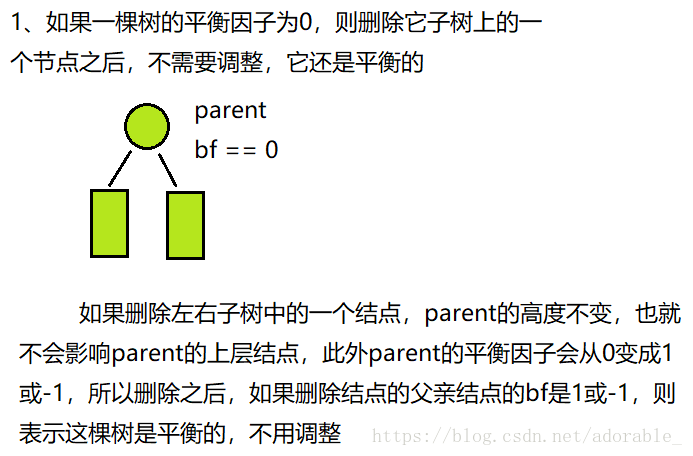
關於左右雙旋，平衡因子有以下幾種情況：

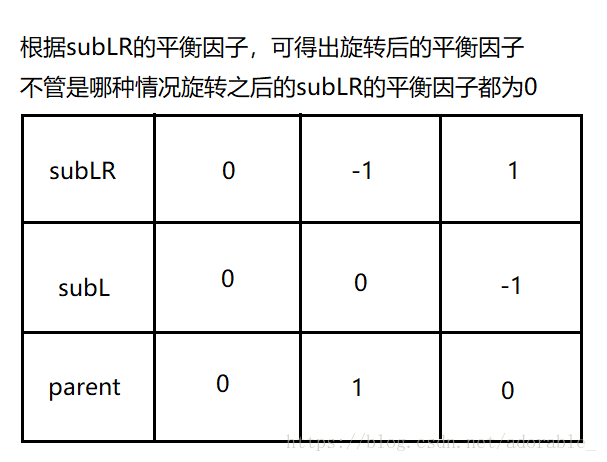
總結：
  如果是左右雙旋的話，經過旋轉之後，各個節點的平衡因子有三種情況。這三種情況與subLR的平衡因子有關。而subLR的平衡因子有三種情況：0、1、-1。如果為0則表示subLR或者是subLR的子樹，此時高度不變。如果是1則表示在subLR的右子樹插入。如果是-1則表示在subLR的左子樹插入。

右左雙旋和左右雙旋為對稱結構，可參照左右雙旋得出。

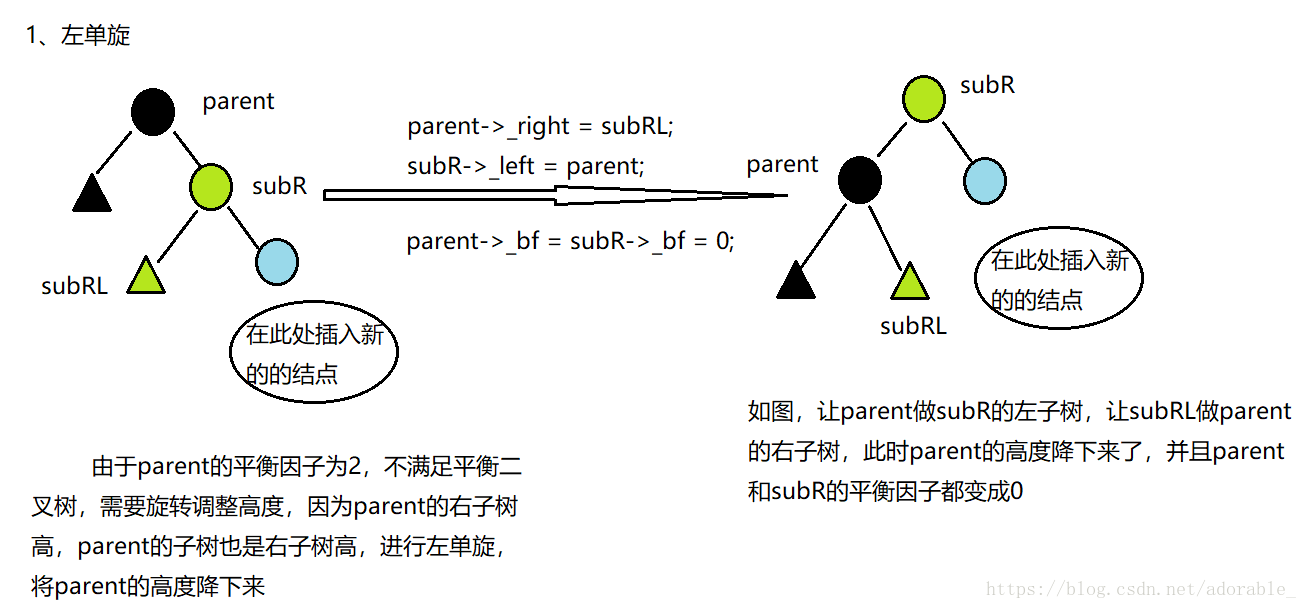
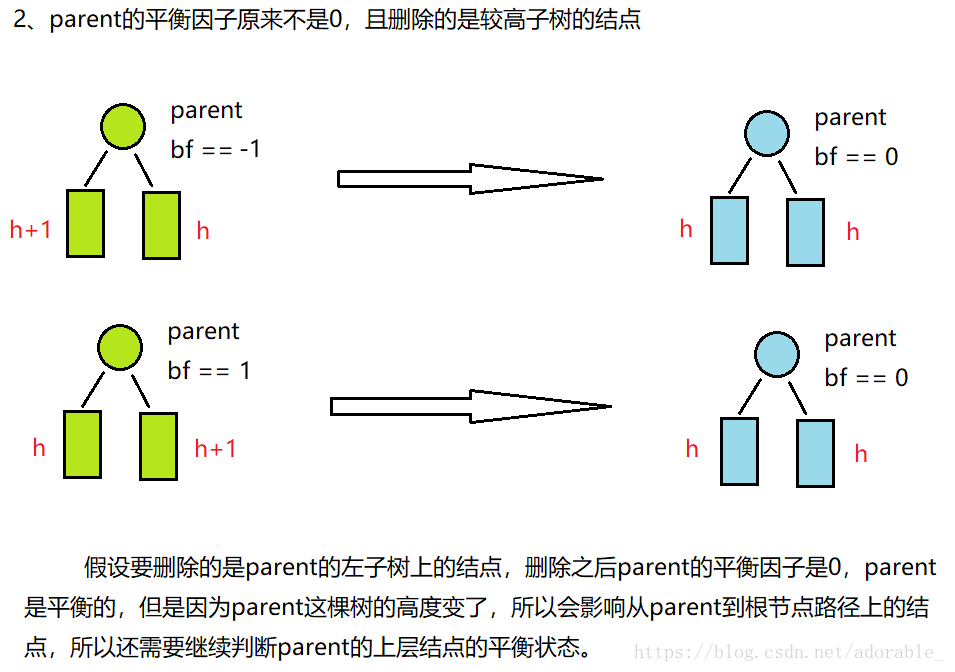
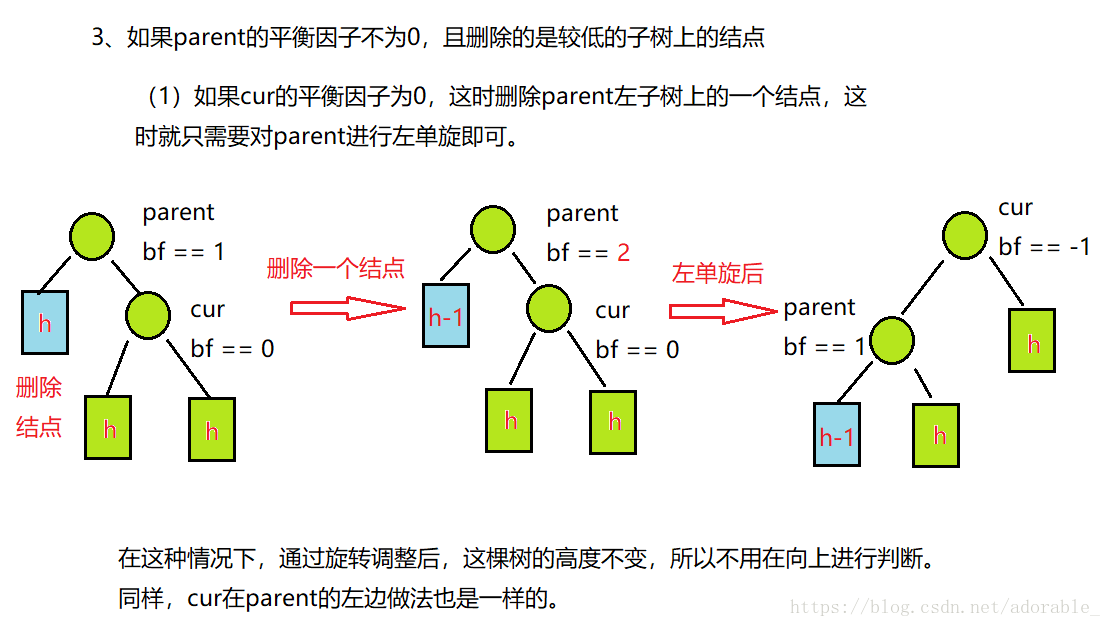
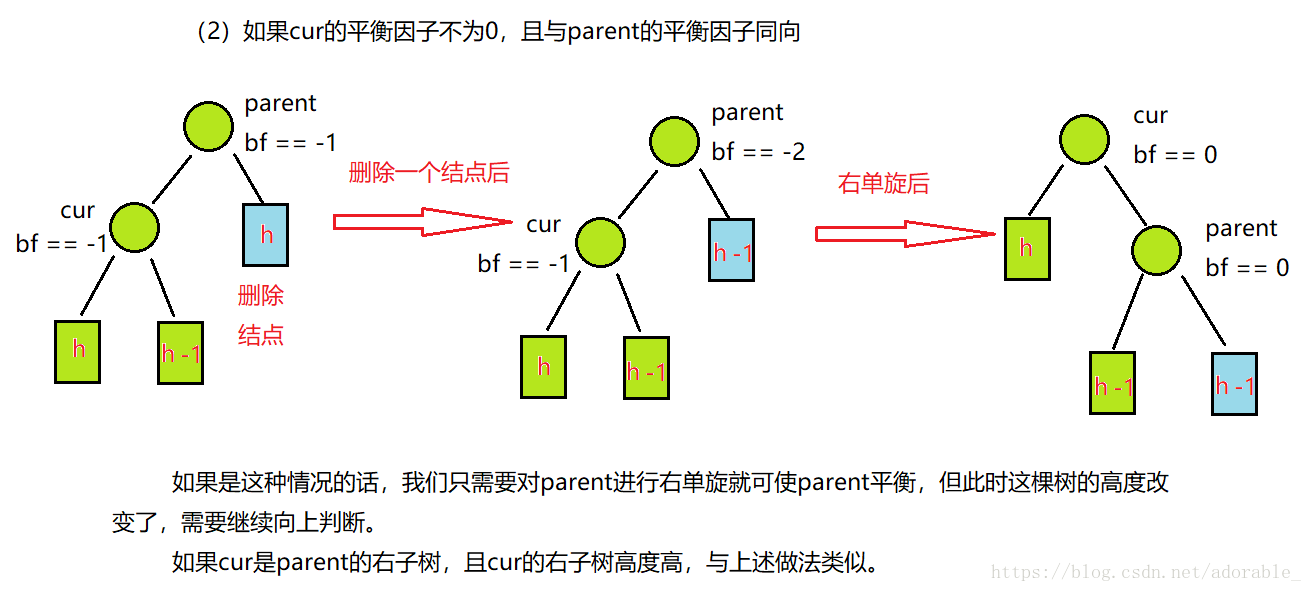
（2）由刪除引起的平衡旋轉
  首先必須明確刪除只會影響從刪除點到根節點路徑上的結點，不會影響刪除點之後的結點。當然刪除與二叉搜尋樹的刪除一樣，將刪除結點有兩個孩子的這種情況轉換成只有一個孩子或者沒有孩子的情況，然後再進行刪除。當然刪除之後樹還要保持平衡。如果只有一個根節點的話直接刪除就行。

基本實現：

#pragma once

#include <iostream>
#include <assert.h>

using namespace std;

template<class K, class V>
 

struct AVLTreeNode
{
    K _key;
    V _value;
    int _bf;       //平衡因子，右子樹高度減去左子樹高度
    AVLTreeNode<K, V>* _left;
    AVLTreeNode<K, V>* _right;
    AVLTreeNode<K, V>* _parent;

    AVLTreeNode(K key, V value)
        :_key(key)
        , _value(value)
        , _bf(0)
        , _left(NULL)
        , _right(NULL)
        , _parent(NULL)
    {}
};

template<class K, class V>
class AVLTree
{
    typedef AVLTreeNode<K, V> Node;
public:
    AVLTree()
        :_root(NULL)
    {}
    AVLTree(const AVLTree<K, V>& tree)
        :_root(NULL)
    {
        _Copy(_root, tree._root);
    }
    AVLTree<K, V>& operator=(const AVLTree<K, V>& tree)
    {
        if (this != &tree)
        {
            AVLTree<K, V> tmp(tree);
            swap(_root, tmp._root)
        }
        return *this;
    }
    ~AVLTree()
    {
        _Destroy(_root);
    }

    bool Insert(const K& key, const V& value)
    {
        if (_root == NULL)
        {
            _root = new Node(key, value);    //空樹時直接插入
            return true;
        }
        Node* parent = NULL;
        Node* cur = _root;
        while (cur)                 //尋找插入的位置
        {
            if (cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_key > key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;       //如果已經存在該元素，則插入失敗
            }
        }
        cur = new Node(key, value);
        if (parent->_key < key)
        {
            parent->_right = cur;
            cur->_parent = parent;
        }
        else
        {
            parent->_left = cur;
            cur->_parent = parent;
        }

        //調節平衡因子
        //1.更新平衡因子
        while (parent)
        {
            if (cur == parent->_right)     //插入節點為parent的右節點，parent平衡因子++
            {
                parent->_bf++;
            }
            else                         //插入節點為parent的左節點，parent平衡因子--
            {
                parent->_bf--;
            }

            if (parent->_bf == 0)         //父親bf==0，表示樹的高度不變，此時就是AVL樹
            {
                break;
            }
            else if (parent->_bf == -1 || parent->_bf == 1)        //子樹高度變了，繼續往上更新
            {
                cur = parent;
                parent = parent->_parent;
            }
            else                        //父親bf==2或-2，不再滿足AVL樹，需要旋轉恢復平衡
            {
                //旋轉
                if (parent->_bf == 2)      //parent的右子樹高
                {
                    if (cur->_bf == 1)     //parent的子樹也是右子樹高，進行左單旋
                    {
                        RotateL(parent);
                    }
                    else                  //parent的子樹的左子樹高，進行右左雙旋
                    {
                        RotateRL(parent);  
                    }
                }
                else                      //parent的左子樹高
                {
                    if (cur->_bf == -1)    //parent的子樹也是左子樹高，進行右單旋
                    {
                        RotateR(parent);
                    }
                    else                  //parent的子樹的右子樹高，進行左右雙旋
                    {
                        RotateLR(parent);
                    }
                }
                break;                    //旋轉完成後樹恢復平衡
            }
        }
        return true;
    } 

    bool Remove(const K& key)
    {
        Node* parent = NULL;
        Node* cur = _root;
        Node* del = NULL;       //指向要刪除的位置
        while (cur)
        {
            if (cur->_key < key)
            {
                cur = cur->_right;
            }
            else if (cur->_key > key)
            {
                cur = cur->_left;
            }
            else
                break;
        }
        if (cur == NULL)      //無此節點，刪除失敗
        {
            return false;
        }
        del = cur;
        //如果要刪除的結點有兩個孩子，則需要找到右子樹的最左結點
        if (cur->_left != NULL && cur->_right != NULL)
        {
            cur = cur->_right;
            while (cur->_left)
            {
                cur = cur->_left;
            }
            del->_key = cur->_key;
            del->_value = cur->_value;
            del = cur;                //交換之後使del指向要刪除的結點
        }
        parent = cur->_parent;         //找到要刪除結點的父親
        if (cur->_left == NULL)        //要刪除結點的左孩子為空，或者都為空
        {
            if (parent == NULL)       //要刪除的是頭結點
            {
                _root = cur->_right;
                if (cur->_right)
                {
                    cur->_right->_parent = NULL;
                }
            }
            else
            {
                if (parent->_left == cur)
                {
                    parent->_left = cur->_right;
                }
                else
                {
                    parent->_right = cur->_right;
                }
                if (cur->_right)
                {
                    cur->_right->_parent = parent;
                }
            }
            cur = del->_right;         //cur更新到要刪除節點的右子樹
        }
        else                          //要刪除節點的右孩子為空，左孩子不為空
        {
            if (parent == NULL)        //要刪除的是頭結點
            {
                _root = cur->_left;
                if (cur->_left)
                {
                    cur->_left->_parent = NULL;
                }
            }
            else
            {
                if (parent->_left == cur)
                {
                    parent->_left = cur->_left;
                }
                else
                {
                    parent->_right = cur->_left;
                }
                if (cur->_left)
                {
                    cur->_left->_parent = parent;
                }
            }
            cur = del->_left;          //cur更新到要刪除結點的左子樹
        }
        //因為要刪除的結點之後的子樹的高度不變，不需修改，需要從parent向上判斷是否平衡
        while (parent)
        {
            //調整parent的平衡因子
            if (parent->_left == cur)           //刪除的是parent的左子樹
            {
                parent->_bf++;
            }
            else
            {
                parent->_bf--;
            }
            if (parent->_bf == 1 || parent->_bf == -1)    //原來平衡，刪除一個後高度不變，整棵樹已經平衡
            {
                break;
            }
            //平衡因子原來不為0，刪除一個後變為0，需要繼續向上尋找
            if (parent->_bf != 0)
            {
                if (cur == NULL)
                {
                    if (parent->_left == NULL)
                    {
                        cur = parent->_right;
                    }
                    else
                    {
                        cur = parent->_left;
                    }
                }
                else
                {
                    if (parent->_left == cur)          //原來parent比較矮的左子樹被刪除，讓cur指向較高的子樹
                    {
                        cur = parent->_right;
                    }
                    else
                    {
                        cur = parent->_left;
                    }
                }
                if (cur->_bf == 0)                   //但旋轉就可以實現平衡
                {
                    if (parent->_bf < 0)             //左子樹高，進行右單旋
                    {
                        RotateR(parent);
                        parent->_bf = 1;
                        parent->_right->_bf = -1;
                    }
                    else                            //右子樹高，進行左單旋
                    {
                        RotateL(parent);
                        parent->_bf = -1;
                        parent->_left->_bf = 1;
                    }
                    break;
                }
                //如果parent與較高子樹同號，進行單旋
                int d = parent->_bf - cur->_bf;
                if (d == 1 || d == -1)
                {
                    if (d == 1)                    //右子樹高，進行左單旋
                    { 
                        RotateL(parent);
                    }
                    else                          //左子樹高，進行右單旋
                    {
                        RotateR(parent);
                    }
                }
                else                              //不同號，進行雙旋
                {
                    if (d == 3)
                    {
                        RotateRL(parent);          //parent的平衡因子2，cur的平衡因子為-1，進行右左雙旋
                    }
                    else
                    {
                        RotateLR(parent);          //parent的平衡因子-2，cur的平衡因子為1，進行左右雙旋
                    }
                }
            }
            cur = parent;
            parent = parent->_parent;
        }
        delete del;
        return true;
    }

    bool Find(const K& key)
    {
        Node* cur = _root;
        while (cur)
        {
            if (cur->_key < key)
            {
                cur = cur->_right;
            }
            else if (cur->_key > key)
            {
                cur = cur->_left;
            }
            else
            {
                return true;
            }
        }
        return false;
    }

    //判斷一顆搜尋二叉樹是不是AVL樹，要求將時間優化到O(N).
    //思路：從根節點向上開始判斷，並將高度傳回上一層。
    bool IsBalance()
    {
        int height = 0;
        return _IsBalance(_root, height);
    }

    void InOrder()
    {
        _InOrder(_root);
        cout << endl;
    }

protected:
    void _Copy(Node* root, Node*& new_root)
    {
        if (root == NULL)
        {
            return;
        }
        Node* node = new Node(root->_key, root->_value);
        node->_bf = root->_bf;
        new_root = node;
        node->_parent = new_root;
        _Copy(root->_left, new_root->_left);
        _Copy(root->_right, new_root->_right);
    }
    void _Destory(Node* root)
    {
        if (root == NULL)
        {
            return;
        }
        _Destory(root->_left);
        _Destory(root->_right);
        delete root;
    }
    void _InOrder(Node* root)
    {
        if (root == NULL)
        {
            return;
        }
        _InOrder(root->_left);
        cout << root->_key << " ";
        _InOrder(root->_right);
    }
    void RotateL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;
        Node* ppNode = parent->_parent;

        parent->_right = subRL;
        if (subRL)
        {
            subRL->_parent = parent;
        }

        subR->_left = parent;
        parent->_parent = subR;

        if (parent == _root)
        {
            _root = subR;
            _root->_parent = NULL;
        }
        else
        {
            if (ppNode->_left == parent)
            {
                ppNode->_left = subR;
            }
            else
            {
                ppNode->_right = subR;
            }
            subR->_parent = ppNode;
        }
        parent->_bf = subR->_bf = 0;         //更新平衡因子
    }
    void RotateR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;
        Node* ppNode = parent->_parent;

        parent->_left = subLR;              //改變指向
        if (subLR)
        {
            subLR->_parent = parent;
        }
        subL->_right = parent;
        parent->_parent = subL;

        if (ppNode == NULL)
        {
            _root = subL;
            _root->_parent = NULL;
        }
        else
        {
            if (ppNode->_left == parent)
            {
                ppNode->_left = subL;
            }
            else
            {
                ppNode->_right = subL;
            }
            subL->_parent = ppNode;
        }
        parent->_bf = subL->_bf = 0;         //更新平衡因子
    }
    void RotateRL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;
        int bf = subRL->_bf;

        RotateR(parent->_right);
        RotateL(parent);

        if (bf == 0)
        {
            parent->_bf = subR->_bf = subRL->_bf = 0;
        }
        else if (bf == 1)
        {
            subR->_bf = 0;
            subRL->_bf = 0;
            parent->_bf = -1;
        }
        else if (bf == -1)
        {
            subR->_bf = 1;
            subRL->_bf = 0;
            parent->_bf = 0;
        }
        else
        {
            assert(false);
        }
    }
    void RotateLR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;
        int bf = subLR->_bf;

        RotateL(parent->_left);
        RotateR(parent);

        if (bf == 0)
        {
            parent->_bf = subL->_bf = subLR->_bf = 0;
        }
        else if (bf == 1)
        {
            subL->_bf = -1;
            subLR->_bf = 0;
            parent->_bf = 0;
        }
        else if (bf == -1)
        {
            subL->_bf = 0;
            subLR->_bf = 0;
            parent->_bf = 1;
        }
        else
        {
            assert(false);
        }
    }
    bool _IsBalance(Node* root, int& height)
    {
        if (root == NULL)
        {
            height = 0;
            return true;
        }
        int leftHeight = 0;
        int rightHeight = 0;
        if (_IsBalance(root->_left, leftHeight) && _IsBalance(root->_right, rightHeight))
        {
            if (rightHeight - leftHeight != root->_bf)
            {
                cout << "平衡因子異常" << root->_key << endl;
                return false;
            }
            height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
            return abs(leftHeight - rightHeight) < 2;
        }
        else
        {
            return false;
        }
    }
private:
    Node* _root;
};

void TestAVLTree()
{
    int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
    AVLTree<int, int> t;
    for (size_t i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
    {
        t.Insert(a[i], i);
        cout << a[i] << ":" << t.IsBalance() << endl;
    }
    t.InOrder();
    cout << t.IsBalance() << endl;
    cout << t.Find(3) << endl;
    t.Remove(15);
    t.InOrder();
    cout << t.IsBalance() << endl;
}