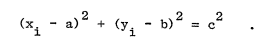關於霍夫變換,  首先看看wiki的介紹

    https://en.wikipedia.org/wiki/Hough_transform

    http://www.iro.umontreal.ca/~mignotte/IFT6150/ComplementCours/HoughTransform.pdf

http://www.dtic.mil/dtic/tr/fulltext/u2/a457992.pdf   -------[Duda,Hart71], 介紹霍夫變換的使用,後面部分將應用拓展到圓

http://comp-eng.binus.ac.id/files/2012/04/D.H.-Ballard-Generalizing-the-Hough-Transform-to-Detect-Arbitrary-Shapes1.pdf

    在圓中, 

    對於任一點,  

未知的引數有三個

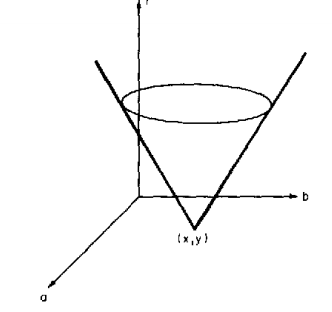
 each figure point will be transformed into a right circularcone in a three-dimensional parameter space.

 If the cones correspondingto many figure points intersect at a single point , say the point (a0, b0, c0),

 then all the figure points lie on the circle defined by those three parameters.

就像這樣,  當然,  這是一個圓心對應半徑從零到無窮變化的圓錐

注: 本篇以上所有圖來源於上面給出連結的最後兩個連結

但是這樣計算量過大, 出現了很多基於霍夫變換的改進演算法

    基於霍夫變換檢測圓, 有 以下兩種情況

1.圓的半徑已知

    前面講的sobel運算元,  因為都連結了wiki,  就沒有細說,  如果不明白,  不妨先看看wiki .

由於計算量太大,  這裡面用了sobel運算元來計算梯度

由sobel運算元,  我們可以求得梯度大小, 以及方向.

當已知半徑估計圓心的時候,  

    對於圓上某一點,  已知梯度方向,  那麼圓心( Xc, Yc)就在該點的法線上距離該點為半徑R

那麼有                    Rcosθ = X - Xc 

而                              cosθ = Gx/ G

所以就有                       Xc = X - R · Gx/ G

不好意思阿在ubuntu下使用特殊符號不太方便,  也沒精力去研究怎麼寫好公式

  類似的                         Yc = Y - R · Gy/ G

這樣,  圓心座標(Xc, Yc)就可以定位出來了

使用霍夫變換檢測圓的具體過程可以是

       1.邊緣檢測

       2.連線邊緣

       3.細化邊緣

       4.對於每個邊緣計算它的圓心

       5.對於這些點簇求平均值,  即為圓心

這個演算法避免了霍夫變換過程中

相對於原本去求edge上每個點以R為半徑的圓(由點構成的圓),  然後求其交點定位為圓心的方法 

   這樣做只需要edge上每個點的法線方向找兩個點,   減少了計算量

實際上opencv上就用了這樣的優化演算法

當然不止這一種改進演算法,  sobel本身就有一定的誤差, 而且受到噪聲的影響

使用具體的演算法還是要查相關論文為好

2.圓的半徑未知

    對於不確定圓的半徑,  對於霍夫變換是要建立3維的parameter space, 就像前面說的那樣.

針對不同的方面(比如計算量阿, 精確度阿,  魯棒性阿)都有基於hough變換的論文

至於效果我也不太清楚,  以前使用過opencv1中的houghcircle, 效果很差

老實說沒看過幾篇論文,  看了也不能馬上理解

還怕寫完這個半個月都過去了

覺得了解了霍夫變換就夠了,  後面文章肯定有基於hough變換的

用到哪裡學到哪裡吧

如果我沒記錯,  opencv裡的hough變換是不能直接檢測橢圓的,   

所以應該會自己試著寫寫演算法看看的,  或者至少知道原理