算法系列之九:計算幾何與圖形學有關的幾種常用演算法(二)
3.6 用向量的叉積判斷直線段是否有交
向量叉積計算的另一個常用用途是直線段求交。求交演算法是計算機圖形學的核心演算法,也是體現速度和穩定性的重要標誌,高效並且穩定的求交演算法是任何一個CAD軟體都必需要重點關注的。求交包含兩層概念,一個是判斷是否相交,另一個是求出交點。直線(段)的求交演算法相對來說是比較簡單的,首先來看看如何判斷兩直線段是否相交。
常規的代數計算通常分三步,首先根據線段還原出兩條線段所在直線的方程,然後聯立方程組求出交點,最後再判斷交點是否線上段區間上。常規的代數方法非常繁瑣,每次都要解方程組求交點,特別是交點不線上段區間的情況,計算交點就是做無用功。計算幾何方法判斷直線段是否有交點通常分兩個步驟完成,這兩個步驟分別是快速排斥試驗和跨立試驗。假設要判斷線段P1P2和線段Q1Q2是否有交點,則:
(1) 快速排斥試驗
設以線段 P1P2 為對角線的矩形為R1, 設以線段 Q1Q2 為對角線的矩形為R2,如果R1和R2不相交,則兩線段不會有交點;
(2) 跨立試驗。
如果兩線段相交,則兩線段必然相互跨立對方,所謂跨立,指的是一條線段的兩端點分別位於另一線段所在直線的兩邊。判斷是否跨立,還是要用到向量叉積的幾何意義。以圖3為例,若P1P2跨立Q1Q2 ,則向量 ( P1 - Q1 ) 和( P2 - Q1 )位於向量( Q2 - Q1 ) 的兩側,即:
( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0
上式可改寫成:
( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0
當 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 時,說明線段P1P2和Q1Q2共線(但是不一定有交點)。同理判斷Q1Q2跨立P1P2的依據是:
( Q1 - P1 ) × ( P2 - P1 ) * ( Q2 - P1 ) × ( P2 - P1 ) < 0
具體情況如下圖所示:

圖3 直線段跨立試驗示意圖
根據向量叉積的幾何意義,跨立試驗只能證明線段的兩端點位於另一個線段所在直線的兩邊,但是不能保證是在另一直線段的兩端,因此,跨立試驗只是證明兩條線段有交點的必要條件,必需和快速排斥試驗一起才能組成直線段相交的充分必要條件。根據以上分析,兩條線段有交點的完整判斷依據就是:1)以兩條線段為對角線的兩個矩形有交集;2)兩條線段相互跨立。
判斷直線段跨立用計算叉積演算法的CrossProduct()函式即可,還需要一個判斷兩個矩形是否有交的演算法。矩形求交也是最簡單的求交演算法之一,原理就是根據兩個矩形的最大、最小座標判斷。圖4展示了兩個矩形沒有交集的各種情況:
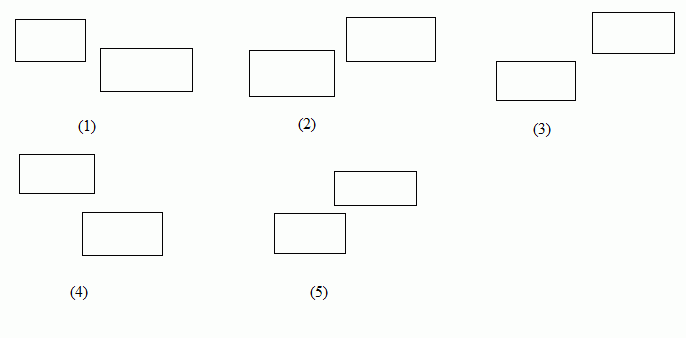
圖4 矩形沒有交集的幾種情況
圖5展示了兩個矩形有交集的各種情況:
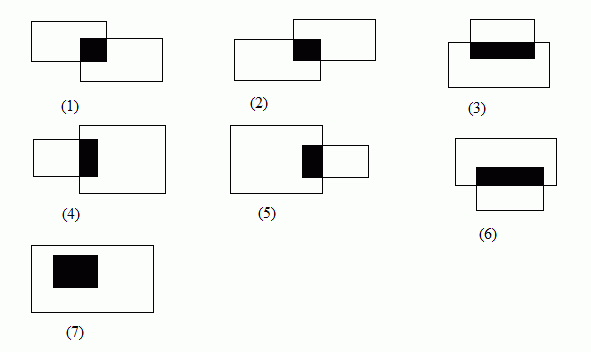
圖5 矩形有交集的幾種情況
從圖4和圖5可以分析出來兩個矩形有交集的幾何座標規律,就是在x座標方向和y座標方向分別滿足最大值最小值法則,簡單解釋這個法則就是每個矩形在每個方向上的座標最大值都要大於另一個矩形在這個座標方向上的座標最小值,否則在這個方向上就不能保證一定有位置重疊。由以上分析,判斷兩個矩形是否相交的演算法就可以如下實現:
186 bool IsRectIntersect(const Rect& rc1, const Rect& rc2) 187 { 188 return ( (std::max(rc1.p1.x, rc1.p2.x) >= std::min(rc2.p1.x, rc2.p2.x)) 189 && (std::max(rc2.p1.x, rc2.p2.x) >= std::min(rc1.p1.x, rc1.p2.x)) 190 && (std::max(rc1.p1.y, rc1.p2.y) >= std::min(rc2.p1.y, rc2.p2.y)) 191 && (std::max(rc2.p1.y, rc2.p2.y) >= std::min(rc1.p1.y, rc1.p2.y)) ); 192 } |
完成了排斥試驗和跨立試驗的演算法,最後判斷直線段是否有交點的演算法就水到渠成了:
204 bool IsLineSegmentIntersect(const LineSeg& ls1, const LineSeg& ls2) 205 { 206 if(IsLineSegmentExclusive(ls1, ls2)) //排斥實驗 207 { 208 return false; 209 } 210 //( P1 - Q1 ) ×'a1?( Q2 - Q1 ) 211 double p1xq = CrossProduct(ls1.ps.x - ls2.ps.x, ls1.ps.y - ls2.ps.y, 212 ls2.pe.x - ls2.ps.x, ls2.pe.y - ls2.ps.y); 213 //( P2 - Q1 ) ×'a1?( Q2 - Q1 ) 214 double p2xq = CrossProduct(ls1.pe.x - ls2.ps.x, ls1.pe.y - ls2.ps.y, 215 ls2.pe.x - ls2.ps.x, ls2.pe.y - ls2.ps.y); 216 217 //( Q1 - P1 ) ×'a1?( P2 - P1 ) 218 double q1xp = CrossProduct(ls2.ps.x - ls1.ps.x, ls2.ps.y - ls1.ps.y, 219 ls1.pe.x - ls1.ps.x, ls1.pe.y - ls1.ps.y); 220 //( Q2 - P1 ) ×'a1?( P2 - P1 ) 221 double q2xp = CrossProduct(ls2.pe.x - ls1.ps.x, ls2.pe.y - ls1.ps.y, 222 ls1.pe.x - ls1.ps.x, ls1.pe.y - ls1.ps.y); 223 224 //跨立實驗 225 return ( (p1xq * p2xq <= 0.0) && (q1xp * q2xp <= 0.0) ); 226 } |
IsLineSegmentExclusive()函式就是呼叫IsRectIntersect()函式根據結果做排斥判斷,此處不再列出程式碼。
3.7 點和多邊形關係的演算法實現
好了,現在我們已經瞭解了向量叉積的意義,以及判斷直線段是否有交點的演算法,現在回過頭看看文章開始部分的討論的問題:如何判斷一個點是否在多邊形內部?根據射線法的描述,其核心是求解從P點發出的射線與多邊形的邊是否有交點。注意,這裡說的是射線,而我們前面討論的都是線段,好像不適用吧?沒錯,確實是不適用,但是我要介紹一種用計算機解決問題時常用的建模思想,應用了這種思想之後,我們前面討論的方法就適用了。什麼思想呢?就是根據問題域的規模和性質抽象和簡化模型的思想,這可不是故弄玄虛,說說具體的思路吧。
計算機是不能表示無窮大和無窮小,計算機處理的每一個數都有確定的值,而且必須有確定的值。我們面臨的問題域是整個實數空間的座標系,在每個維度上都是從負無窮到正無窮,比如射線,就是從座標系中一個明確的點到無窮遠處的連線。這就有點為難計算機了,為此我們需要簡化問題的規模。假設問題中多邊形的每個點的座標都不會超過(-10000.0, +10000.0)區間(比如我們常見的圖形輸出裝置都有大小的限制),我們就可以將問題域簡化為(-10000.0, +10000.0)區間內的一小塊區域,對於這塊區域來說,>= 10000.0就意味著無窮遠。你肯定已經明白了,數學模型經過簡化後,演算法中提到的射線就可以理解為從模型邊界到內部點P之間的線段,前面討論的關於線段的演算法就可以使用了。
射線法的基本原理是判斷由P點發出的射線與多邊形的交點個數,交點個數是奇數表示P點在多邊形內(在多邊形的邊上也視為在多邊形內部的特殊情況),正常情況下經過點P的射線應該如圖6(a)所示那樣,但是也可能碰到多種非正常情況,比如剛好經過多邊形一個定點的情況,如圖6 (b),這會被誤認為和兩條邊都有交點,還可能與某一條邊共線如圖6 (c)和(d),共線就有無窮多的交點,導致判斷規則失效。還要考慮凹多邊形的情況,如圖6(e)。
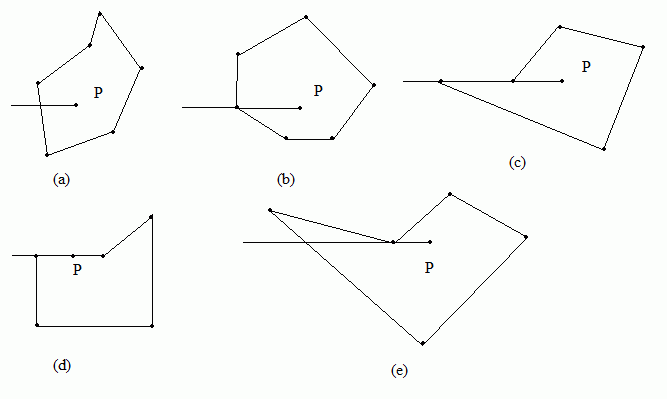
圖6 射線法可能遇到的各種交點情況
針對這些特殊情況,在對多邊形的每條邊進行判斷時,要考慮以下這些特殊情況,假設當前處理的邊是P1P2,則有以下原則:
1)如果點P在邊P1P2上,則直接判定點P在多邊形內;
2)如果從P發出的射線正好穿過P1或者P2,那麼這個交點會被算作2次(因為在處理以P1或P2為端點的其它邊時可能已經計算過這個點了),對這種情況的處理原則是:如果P的y座標與P1、P2中較小的y座標相同,則忽略這個交點;
3)如果從P發出的射線與P1P2平行,則忽略這條邊;
對於第三個原則,需要判斷兩條直線是否平行,通常的方法是計算兩條直線的斜率,但是本演算法因為只涉及到直線段(射線也被模型簡化為長線段了),就簡化了很多,判斷直線是否水平,只要比較一下線段起始點的y座標是否相等就行了,而判斷直線是否垂直,也只要比較一下線段起始點的x座標是否相等就行了。
應用以上原則後,掃描線法判斷點是否在多邊形內的演算法流程就完整了,圖7就是演算法的流程圖:
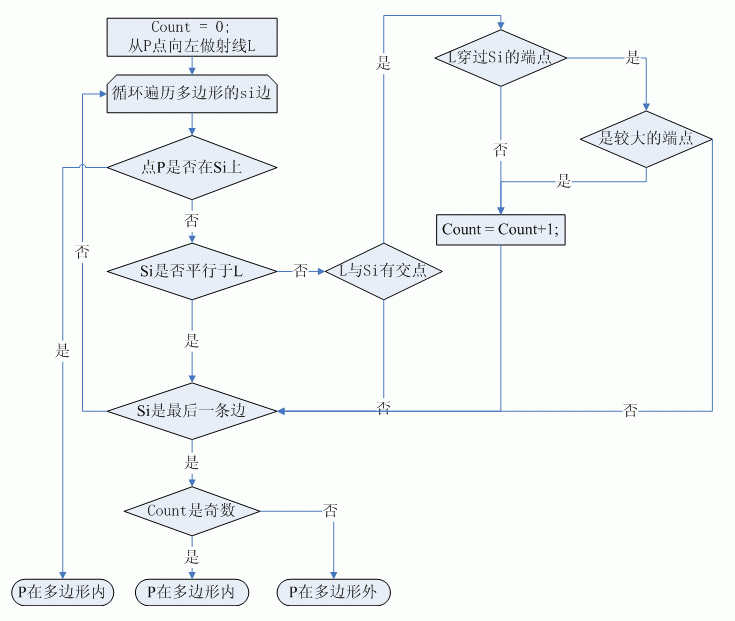
最終掃描線法判斷點是否在多邊形內的演算法實現如下:
228 bool IsPointInPolygon(const Polygon& py, const Point& pt) 229 { 230 assert(py.IsValid()); /*只考慮正常的多邊形,邊數>=3*/ 231 232 int count = 0; 233 LineSeg ll = LineSeg(pt, Point(-INFINITE, pt.y)); /*射線L*/ 234 for(int i = 0; i < py.GetPolyCount(); i++) 235 { 236 /*當前點和下一個點組成線段P1P2*/ 237 LineSeg pp = LineSeg(py.pts[i], py.pts[(i + 1) % py.GetPolyCount()]); 238 if(IsPointOnLineSegment(pp, pt)) 239 { 240 return true; 241 } 242 243 if(!pp.IsHorizontal()) 244 { 245 if((IsSameFloatValue(pp.ps.y, pt.y)) && (pp.ps.y > pp.pe.y)) 246 { 247 count++; 248 } 249 else if((IsSameFloatValue(pp.pe.y, pt.y)) && (pp.pe.y > pp.ps.y)) 250 { 251 count++; 252 } 253 else 254 { 255 if(IsLineSegmentIntersect(pp, ll)) 256 { 257 count++; 258 } 259 } 260 } 261 } 262 263 return ((count % 2) == 1); 264 } |
在圖形學領域實施的真正工程程式碼,通常還會增加一個多邊形的外包矩形快速判斷,對點根本就不在多邊形周圍的情況做快速排除,提高演算法效率。這又涉及到求多邊形外包矩形的演算法,這個演算法也很簡單,就是遍歷多邊形的所有節點,找出各個座標方向上的最大最小值。以下就是求多邊形外包矩形的演算法:
266 void GetPolygonEnvelopRect(const Polygon& py, Rect& rc) 267 { 268 assert(py.IsValid()); /*只考慮正常的多邊形,邊數>=3*/ 269 270 double minx = py.pts[0].x; 271 double maxx = py.pts[0].x; 272 double miny = py.pts[0].y; 273 double maxy = py.pts[0].y; 274 for(int i = 1; i < py.GetPolyCount(); i++) 275 { 276 if(py.pts[i].x < minx) 277 minx = py.pts[i].x; 278 if(py.pts[i].x > maxx) 279 maxx = py.pts[i].x; 280 if(py.pts[i].y < miny) 281 miny = py.pts[i].y; 282 if(py.pts[i].y > maxy) 283 maxy = py.pts[i].y; 284 } 285 286 rc = Rect(minx, miny, maxx, maxy); 287 } |
除了掃描線法,還可以通過多邊形邊的法向量方向、多邊形面積以及角度和等方法判斷點與多邊形的關係。但是這些演算法要麼只支援凸多邊形,要麼需要複雜的三角函式運算(多邊形邊數小於44時,可採用近似公式計算夾角和,避免三角函式運算),使用的範圍有限,只有掃描線法被廣泛應用。
至此,本文的內容已經完結,以上通過對點與矩形、點與圓、點與直線以及點與多邊形位置關係判斷演算法的講解,向大家展示了幾種常見的計算幾何演算法實現,用簡短而易懂的程式碼剖析了這些演算法的實質。下一篇將介紹計算機圖形學中最基本的直線生成演算法。
參考資料:
【1】計算幾何:演算法設計與分析 周培德 清華大學出版社 2005年
【2】計算幾何:演算法與應用 德貝爾赫(鄧俊輝譯) 清華大學出版社 2005年
【3】演算法導論 Thomas H.Cormen等(潘金貴等譯) 機械工業出版社 2006年
【4】計算機圖形學 孫家廣、楊常貴 清華大學出版社 1995年
