修改預訂樹遍歷

現在，我們來看看儲存樹的另一種方法。遞迴可能很慢，所以我們寧可不使用遞迴函式。我們也希望最小化資料庫查詢的數量。我們最好只對每個活動進行一次查詢。

我們將從水平的方式展開我們的樹。從根節點（'Food'）開始，並在其左邊寫1。按照樹進行“水果”，並在其旁邊寫一個2。這樣，在每個節點的左側和右側寫一個數字時，沿著樹的邊緣走（遍歷）。最後一個數字寫在“食物”節點的右側。在這個影象中，您可以看到整個編號的樹，還有幾個箭頭來指示編號順序。

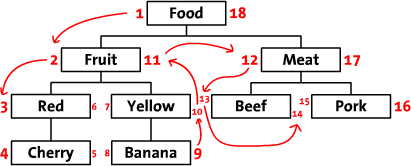
我們會將這些數字左右呼叫（例如，“食物”的左側值為1，正確的值為18）。您可以看到，這些數字表示每個節點之間的關係。因為“紅”有數字3和6，它是1-18“食物”節點的後裔。

在我們繼續之前，讓我們看看這些值在我們的表中如何：

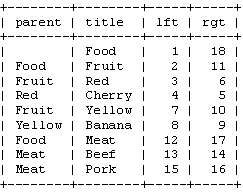
請注意，“left”和“right”這個詞在SQL中有特殊的含義。因此，我們必須使用'lft'和'rgt'來標識列。還要注意，我們不再需要“父”列了。我們現在有lft和rgt值來儲存樹結構。

檢索樹

如果要使用具有左右值的表顯示樹，則首先必須標識要檢索的節點。例如，如果您想要“水果”子樹，則必須僅選擇左側值在2和11之間的節點。在SQL中，這將是：

SELECT * FROM tree WHERE lft BETWEEN 2 AND 11;
 

那回報：

那就是：一個查詢中的一棵樹。要像我們的遞迴函式那樣顯示這個樹，我們必須向此查詢新增一個ORDER BY子句。如果您從表中新增和刪除行，則表可能不會處於正確的順序。因此，我們應該按照左邊的值排列。

SELECT * FROM tree WHERE lft BETWEEN 2 AND 11 ORDER BY lft ASC;

剩下的唯一問題就是縮排。

為了顯示樹狀結構，兒童的縮寫比父母稍微縮小一點。我們可以通過保持一堆正確的值來做到這一點。每次從一個節點的子節點開始，您將該節點的正確值新增到堆疊中。您知道該節點的所有子節點都具有小於父節點正確值的正確值，因此通過將當前節點的正確值與堆疊中的最右邊節點進行比較，可以看到是否仍然展示該家長的孩子。

<?php  
function display_tree($root) {  
    // retrieve the left and right value of the $root node  
    $result = mysql_query('SELECT lft, rgt FROM tree '.  
                           'WHERE title="'.$root.'";');  
    $row = mysql_fetch_array($result);  
  
    // start with an empty $right stack  
    $right = array();  
  
    // now, retrieve all descendants of the $root node  
    $result = mysql_query('SELECT title, lft, rgt FROM tree '.  
                           'WHERE lft BETWEEN '.$row['lft'].' AND '.  
                           $row['rgt'].' ORDER BY lft ASC;');  
  
    // display each row  
    while ($row = mysql_fetch_array($result)) {  
        // only check stack if there is one  
        if (count($right)>0) {  
            // check if we should remove a node from the stack  
            while ($right[count($right)-1]<$row['rgt']) {  
                array_pop($right);  
            }  
        }  
  
        // display indented node title  
        echo str_repeat('  ',count($right)).$row['title']."n";  
  
        // add this node to the stack  
        $right[] = $row['rgt'];  
    }  
}  
?>

如果你執行這個程式碼，你將得到與上面討論的遞迴函式完全相同的樹。我們的新功能可能會更快：它不是遞迴的，它只使用兩個查詢。

節點的路徑

使用這種新演算法，我們還必須找到一種新方式來獲取特定節點的路徑。要獲得這個路徑，我們需要一個列表，該節點的所有祖先。

用我們新的表格結構，這真的不是很大的工作。例如，當您檢視4-5個“櫻桃”節點時，您會看到所有祖先的左值小於4，而所有正確的值都大於5.要獲取所有祖先，我們可以使用這個查詢：

SELECT title FROM tree WHERE lft < 4 AND rgt > 5 ORDER BY lft ASC;

請注意，就像我們之前的查詢一樣，我們必須使用ORDER BY子句對節點進行排序。此查詢將返回：

+-------+
| title |
+-------+
| Food  |
| Fruit |
| Red   |
+-------+

我們現在只需要加入行以獲得“櫻桃”的路徑。

多少後裔

如果你給我一個節點的左右值，我可以通過使用一點數學來告訴你有多少個後代。

當每個後代用2增加節點的正確值時，可以通過以下方式計算後代數：

descendants = (right – left - 1) / 2

有了這個簡單的公式，我可以告訴你，2-11“果實”節點有4個後代節點，8-9個“香蕉”節點只是一個小孩，而不是一個父母。