以下是閱讀了《演算法導論》後，對雜湊表的一些總結：

雜湊表又叫散列表，是實現字典操作的一種有效資料結構。雜湊表的查詢效率極高，在沒有衝突（後面會介紹）的情況下可做到一次存取便能得到所查記錄，在理想情況下，查詢一個元素的平均時間為O(1)（最差情況下散列表中查詢一個元素的時間與連結串列中查詢的時間相同：O(n)，但實際情況中一般散列表的效能是比較好的）。

雜湊表就是描述key—value對的對映問題的資料結構，更詳細的描述是：在記錄的儲存位置和它的關鍵字之間建立一個確定的對應關係h，使每個關鍵字與雜湊表中唯一一個儲存位置相對應。我們稱這個對應關係f為雜湊/雜湊函式，這個儲存結構即為雜湊/散列表。

一、直接定址表

當關鍵字的全域U比較小時，直接定址是一種簡單而有效的技術，它的雜湊函式很簡單：f(key) = key，即關鍵字大小直接與元素所在的表位置序號相等。如果關鍵字不是整數，我們需要通過某種手段將其轉換為整數，比如可以將字元關鍵字轉化為其在字母表中的序號作為關鍵字。直接定址法的優點是不會出現兩個關鍵字對應到同一個地址的情況（即不會出現f（key1） = f(key2)的情況），因此不用處理衝突。但是，直接定址表也有著天然的侷限性，即如果全域U很大，則在一臺標準的計算機可用記憶體容量中，要儲存大小為U的一張表並不實際。

二、散列表

上面說到，在處理實際資料的時候，全域U往往會很大，則在一臺標準的計算機可用記憶體容量中，要儲存大小為U的一張表也許不太實際，此時實際需要儲存的關鍵字集合K

散列表T通過雜湊函式f計算出關鍵字key在表中的位置，這些位置被稱為“槽”。雜湊函式f將關鍵字域U對映到散列表T[0...m-1]的槽位上。由於關鍵字的個數要大於槽的個數，這裡會出現一個問題：若干個關鍵字可能對映到了表的同一個位置處，我們稱這種情形為衝突。我們希望散列表在節省空間的同時，其效能要接近於O(1)，因此需要儘量避免衝突，通常的策略是儘可能地設計更好的雜湊函式f，將關鍵字儘可能隨機地對映到散列表的每個位置上（為什麼說盡可能？因為這裡關鍵字的個數|U|肯定大於散列表的槽個數m，因此至少有兩個關鍵字被對映到同一個槽中，只依靠雜湊函式f

三、雜湊函式

雜湊函式的構造方法很多，最好的情況是：對於關鍵字結合中的任一個關鍵字，經雜湊函式對映到地址集合中任何一個地址的概率相等，也就是說，關鍵字經過雜湊函式得到一個隨機的地址，以便使一組關鍵字的雜湊地址均勻分佈在整個地址空間中，從而減少衝突。同樣，由於多數雜湊函式都是假定關鍵字的全域為自然數集N={0、1、2….}，因此所給關鍵字如果不是自然數，就要先想辦法將其轉換為自然數。下面我們就來看常用的雜湊函式。

1.直接定址法

對應前面的直接定址表，關鍵字與雜湊表中的地址有著一一對應關係，因此不需要處理衝突。

2.除法雜湊法

雜湊函式：f(key) = key % m

函式對所給關鍵字key取餘，這裡 m 必須不能大於雜湊表的長度len，通常 m 可取一個不太接近2的整數次冪的素數。

3.乘法雜湊法

用關鍵字key乘上A（0 < A < 1），取出其小數部分，然後用 m 乘以小數的值，再向下取整，該函式寫為：f(key) = floor(m * (key * A % 1))

其中，(key * A % 1)是取(key * A)的小數部分，該函式涉及到引數A的取值問題。Knuth認為，A = (sqrt(5)-1)/2 = 0.6180339877...是個比較理想的值，事實上，該點就是黃金分割點。

除法雜湊法和乘法雜湊法是較為常用的雜湊函式設計方法，事實上方法還有很多種，如全域雜湊法、摺疊法、數字分析法等，更多的介紹請參考相關書籍。

四、衝突處理

前面提到，為了節省空間，表中槽的數目小於關鍵字的數目，只是通過設計好的雜湊函式不可能完全避免衝突。下面介紹兩種解決衝突的方法：連結法和開放定址法。

1.連結法(chaining)

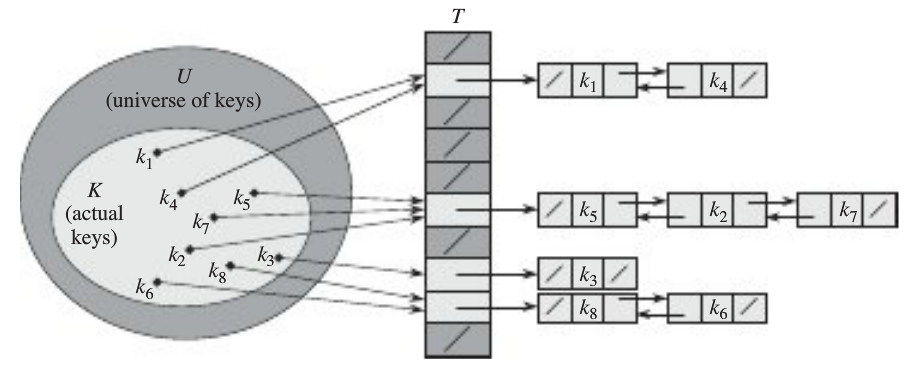
連結法的思路很簡單：如果多個關鍵字對映到了雜湊表的同一個位置處（將這些關鍵字稱為同義詞），則將這些同義詞記錄在同一個線性連結串列中，該槽有一個指標，它指向儲存所有雜湊到該槽的元素的連結串列表頭，如下圖所示：

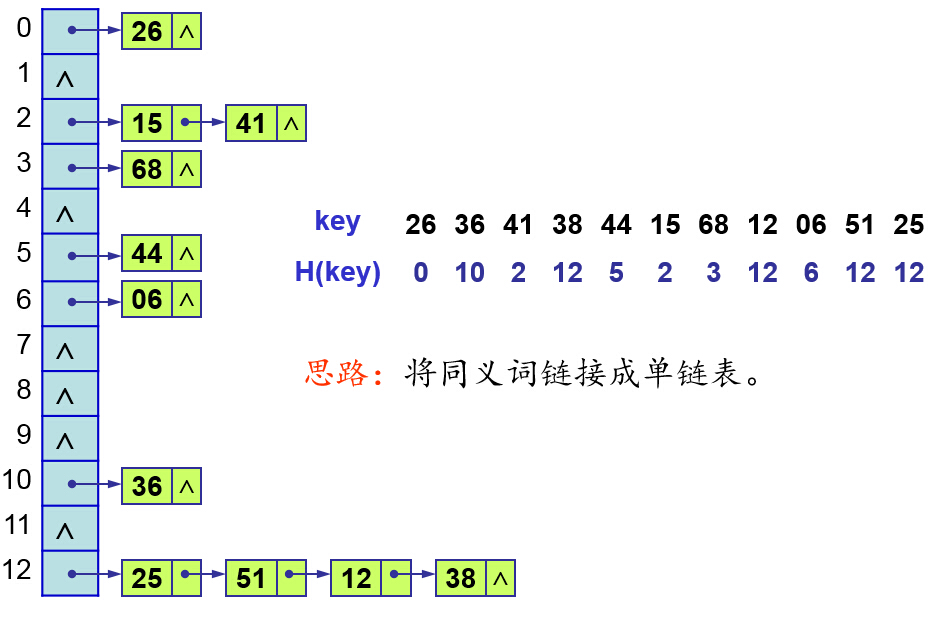
圖中，關鍵字k1和k4對映到了雜湊表的同一個位置處，k5、k2、k7對映到了雜湊表的同一個位置處。《演算法導論》提到，為了更快地刪除某個元素，可以將連結串列設計為雙向連結串列。如果表是單鏈接的，則為了刪除元素x，首先必須在表T[h(x,key)]中找到元素x，然後通過更改x的前去元素的next屬性，把x從連結串列中刪除。在單鏈表的情況下，刪除和查詢操作的漸近執行時間相同。另一個例子如下：

2.開放定址法(open addressing)

在開放定址法中，所有的元素都存放在散列表中，也即是說，每個表項或包含動態集合的一個元素，或為空，不再使用連結串列。雜湊表中的槽t不僅向雜湊函式值等於t的同義詞開放，而且向雜湊函式值不等於t的記錄開放，允許以“搶佔”的方式爭取雜湊地址。

該方法採用如下公式記性再雜湊：

F(key,i) = (f(key) + di) % len

其中，f(key)為雜湊函式，len為雜湊表長，di為增量序列，它可能有如下三種情況：

• di = 1,2,3...m-1

• di = 1，-1，4，-4，9，-9...k^2，-k^2

• di為偽隨機序列

採用第一種序列的叫做線性探測再雜湊，採用第二種序列的叫做二次探測再雜湊，採用第三種序列的叫做隨機探測再雜湊。說白了，就是在發生衝突時，將關鍵字應該放入的位置向前或向後移動若干位置，比如採取第一種序列時，如果遇到衝突，就向後移動一個位置來檢測，如果還發生衝突，繼續向後移動，直到遇到一個空槽，則將該關鍵字插入到該位置處。

線性探測比較容易實現，但是它存在一個問題，稱為一次群集。隨著連續被佔用的槽不斷增加，平均查詢時間也隨之不斷增加，群集現象很容易出現，這是因為當一個空槽前有i個滿槽時，該空槽為下一個將被佔用的概率為(di+1)len。

同樣採用二次探測的方法，會產生二次群集，因為每次遇到衝突時，尋找插入位置時都是在跳躍性前進或後退，因此這個相對於一次群集來說，比較輕度。

五、一些例子

已知關鍵字序列：26，36，41，38，44，15，68，12，06，51，25。

用除法雜湊法構造雜湊函式，線性探測再雜湊法解決衝突。現在需要：①建雜湊表；②求查詢成功和失敗的平均搜尋長度(ASL)。

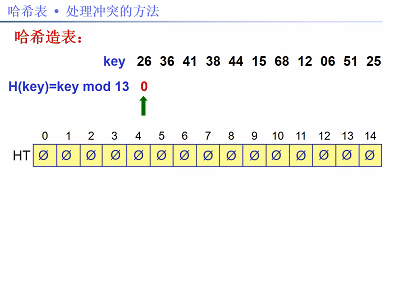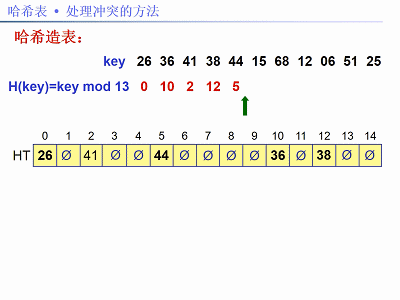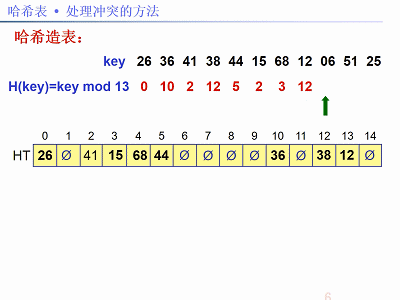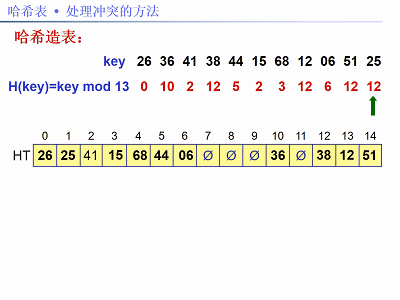
解法：題中關鍵字個數n = 11，設裝載因子α = 0.75，m = n / α，取m為素數13。雜湊函式：f(key) = key % 13，以下圖片給出了建雜湊表的步驟：

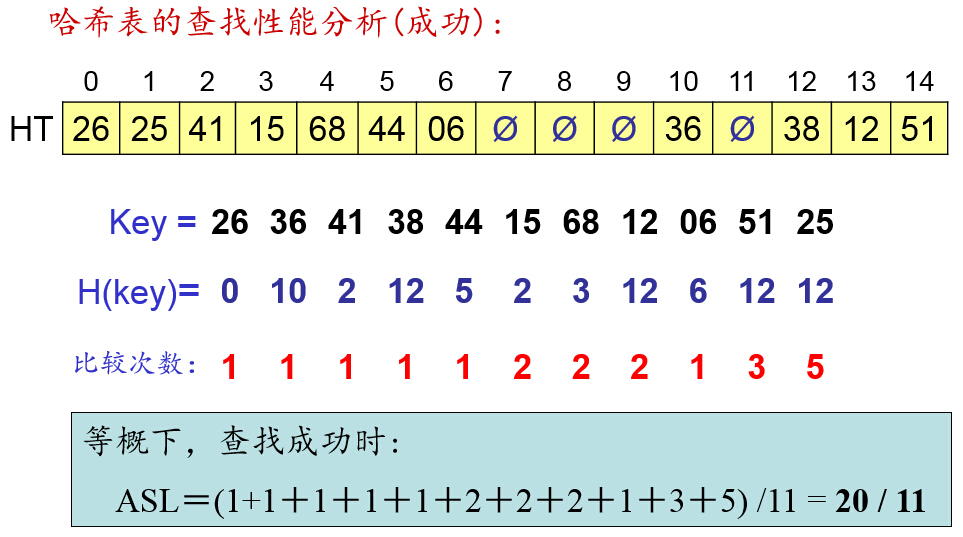
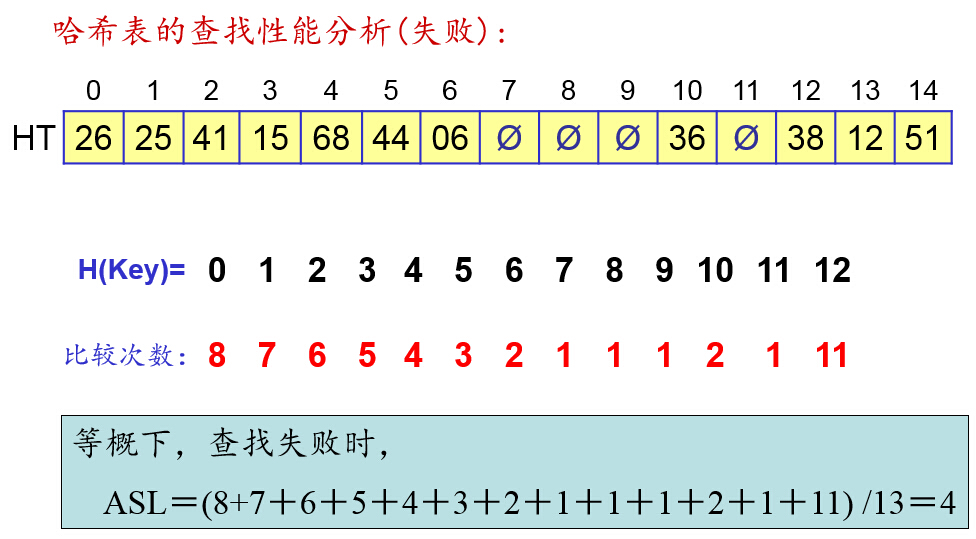
雜湊表的查詢效能分析：

六、程式碼實現

下面用程式碼實現一個雜湊表，這裡採用連結法來處理衝突，描述資料結構的標頭檔案的程式碼如下：

#define M 7     //雜湊函式中的除數,必須小於等於表長
typedef int ElemType;

// 該雜湊表採用連結法解決衝突問題

typedef struct Node 
{   //Node為連結串列節點的資料結構
    ElemType data;
    struct Node *next;
}Node,*pNode;

// 雜湊表每個槽的資料結構
typedef struct HashNode
{   
    pNode first;    // first指向連結串列的第一個節點
}HashNode,*HashTable;

// 建立雜湊表
HashTable create_HashTable(int);

// 在雜湊表中查詢資料
pNode search_HashTable(HashTable, ElemType);

// 插入資料到雜湊表
bool insert_HashTable(HashTable,ElemType);

// 從雜湊表中刪除資料
bool delete_HashTable(HashTable,ElemType);

// 銷燬雜湊表
void destroy_HashTable(HashTable,int);

首先建立一個空雜湊表，而然後執行插入、刪除、查詢等操作，最後銷燬雜湊表，雜湊表的實現程式碼如下：

#include<stdio.h>
#include<stdlib.h>
#include "data_structure.h"

// 建立n個槽的雜湊表
HashTable create_HashTable(int n)
{
    int i;
    HashTable hashtable = (HashTable)malloc(n*sizeof(HashNode));
    if(!hashtable)
    {
        printf("hashtable malloc faild,program exit...");
        exit(-1);
    }

    // 將雜湊表置空
    for(i=0;i<n;i++)
        hashtable[i].first = NULL;

    return hashtable;
}

// 在雜湊表中查詢資料，雜湊函式為H(key)=key % M
// 查詢成功則返回在連結串列中的位置
// 查詢不成功則返回NULL
pNode search_HashTable(HashTable hashtable, ElemType data)
{
    if(!hashtable)
        return NULL;

    pNode pCur = hashtable[data%M].first;
    while(pCur && pCur->data != data)
        pCur = pCur->next;

    return pCur;
}

// 向雜湊表中插入資料，雜湊函式為H(key)=key%M
// 如果data已存在，則返回fasle
// 否則，插入對應連結串列的最後並返回true
bool insert_HashTable(HashTable hashtable,ElemType data)
{
    // 如果已經存在，返回false
    if(search_HashTable(hashtable,data))
        return false;

    // 否則為插入資料分配空間
    pNode pNew = (pNode)malloc(sizeof(Node));
    if(!pNew)
    {
        printf("pNew malloc faild,program exit...");
        exit(-1);
    }
    pNew->data = data;
    pNew->next = NULL;

    // 將節點插入到對應連結串列的最後
    pNode pCur = hashtable[data%M].first;
    if(!pCur)   // 插入位置為連結串列第一個節點的情況
        hashtable[data%M].first = pNew;
    else    // 插入位置不是連結串列第一個節點的情況
    {   // 只有用pCur->next才可以將pNew節點連到連結串列上，
        // 用pCur連不到連結串列上，而是連到了pCur上
        // pCur雖然最終指向連結串列中的某個節點，但是它並不在連結串列中
        while(pCur->next)
            pCur = pCur->next;
        pCur->next = pNew;
    }

    return true;
}

// 從雜湊表中刪除資料，雜湊函式為H(key)=key % M
// 如果data不存在，則返回fasle，
// 否則，刪除並返回true
bool delete_HashTable(HashTable hashtable,ElemType data)
{
    // 如果沒查詢到，返回false
    if(!search_HashTable(hashtable,data))
        return false;
    // 否則，刪除資料
    pNode pCur = hashtable[data%M].first;
    pNode pPre = pCur;  // 被刪節點的前一個節點,初始值與pCur相同
    if(pCur->data == data)  // 被刪節點是連結串列的第一個節點的情況
        hashtable[data%M].first = pCur->next;
    else
    {   // 被刪節點不是第一個節點的情況
        while(pCur && pCur->data != data)
        {
            pPre = pCur;
            pCur = pCur->next;
        }
        pPre->next = pCur->next;
    }
    free(pCur);
    pCur = 0;
    return true;
}

// 銷燬槽數為n的雜湊表
void destroy_HashTable(HashTable hashtable,int n)
{
    int i;
    // 先逐個連結串列釋放
    for(i=0;i<n;i++)
    {
        pNode pCur = hashtable[i].first;
        pNode pDel = NULL;
        while(pCur)
        {
            pDel = pCur;
            pCur = pCur->next;
            free(pDel);
            pDel = 0;
        }
    }
    // 最後釋放雜湊表
    free(hashtable);
    hashtable = 0;
}

最後測試程式碼：

#include<stdio.h>
#include "data_structure.h"

int main()
{
    int len = 15;   // 雜湊表長，亦即表中槽的數目
    printf("We set the length of hashtable %d\n",len);

    //建立雜湊表並插入資料
    HashTable hashtable = create_HashTable(len);
    if(insert_HashTable(hashtable,1))
        printf("insert 1 success\n");
    else 
        printf("insert 1 fail,it is already existed in the hashtable\n");
    if(insert_HashTable(hashtable,8))
        printf("insert 8 success\n");
    else 
        printf("insert 8 fail,it is already existed in the hashtable\n");
    if(insert_HashTable(hashtable,3))
        printf("insert 3 success\n");
    else 
        printf("insert 3 fail,it is already existed in the hashtable\n");
    if(insert_HashTable(hashtable,10))
        printf("insert 10 success\n");
    else 
        printf("insert 10 fail,it is already existed in the hashtable\n");
    if(insert_HashTable(hashtable,8))
        printf("insert 8 success\n");
    else 
        printf("insert 8 fail,it is already existed in the hashtable\n");

    //查詢資料
    pNode pFind1 = search_HashTable(hashtable,10);
    if(pFind1)
        printf("find %d in the hashtable\n",pFind1->data);      
    else 
        printf("not find 10 in the hashtable\n");
    pNode pFind2 = search_HashTable(hashtable,4);
    if(pFind2)
        printf("find %d in the hashtable\n",pFind2->data);      
    else 
        printf("not find 4 in the hashtable\n");

    //刪除資料
    if(delete_HashTable(hashtable,1))
        printf("delete 1 success\n");
    else 
        printf("delete 1 fail");
    pNode pFind3 = search_HashTable(hashtable,1);
    if(pFind3)
        printf("find %d in the hashtable\n",pFind3->data);      
    else 
        printf("not find 1 in the hashtable,it has been deleted\n");

    // 銷燬雜湊表
    destroy_HashTable(hashtable,len);
    return 0;
}

七、參考資料