2. 程式人生 > >Lanczos插值，最鄰近插值，雙線性二次插值，三次插值

Lanczos插值，最鄰近插值，雙線性二次插值，三次插值

阿新 • • 發佈：2019-01-30

本文為轉載，原部落格地址：http://blog.csdn.net/trent1985/article/details/45150677

[研究內容]

目前比較常用的幾種插值演算法

[正文]

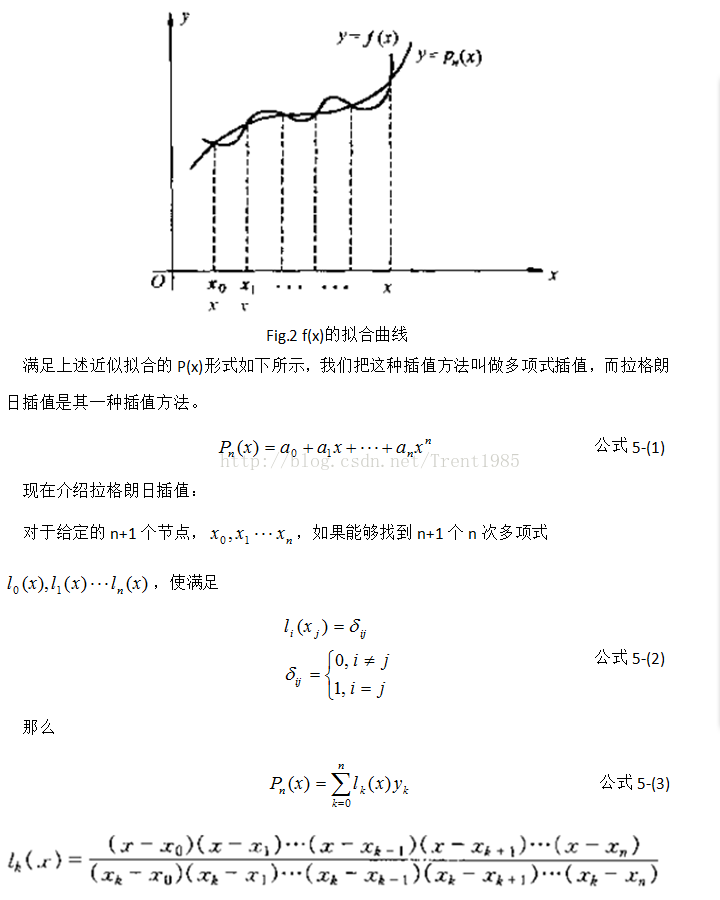
目前比較常用的插值演算法有這麼幾種：最鄰近插值，雙線性二次插值，三次插值，

Lanczos插值等等，今天我們來對比一下這幾種插值效果的優劣。

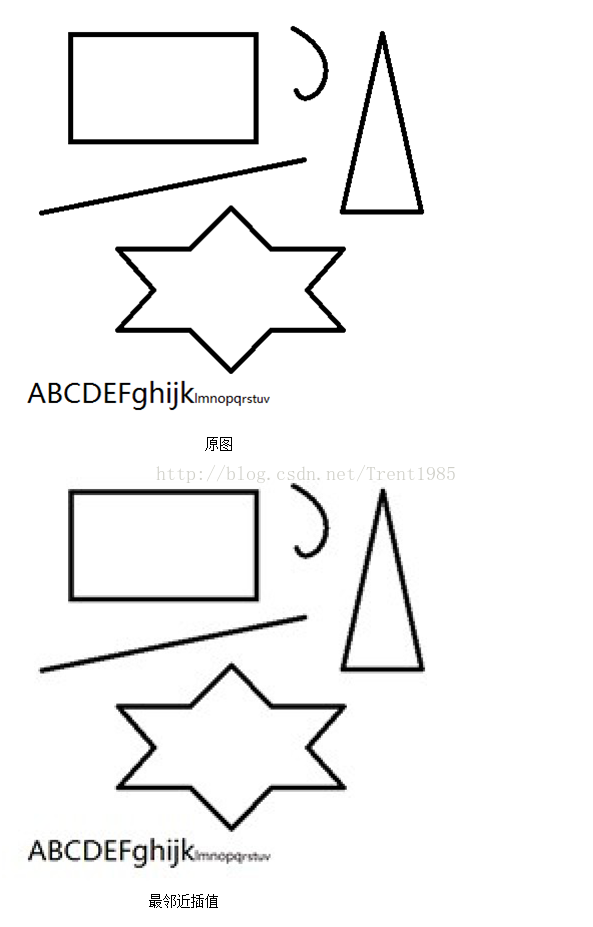
1，最鄰近插值

    最鄰近插值演算法也叫做零階插值演算法，主要原理是讓輸出畫素的畫素值等於鄰域內

離它距離最近的畫素值。例如下圖中所示，P1距離0灰度值畫素的距離小於100灰度值的

距離，因此，P1位置的插值畫素為0。這個演算法的優點是計算簡單方便，缺點是影象容

易出現鋸齒。

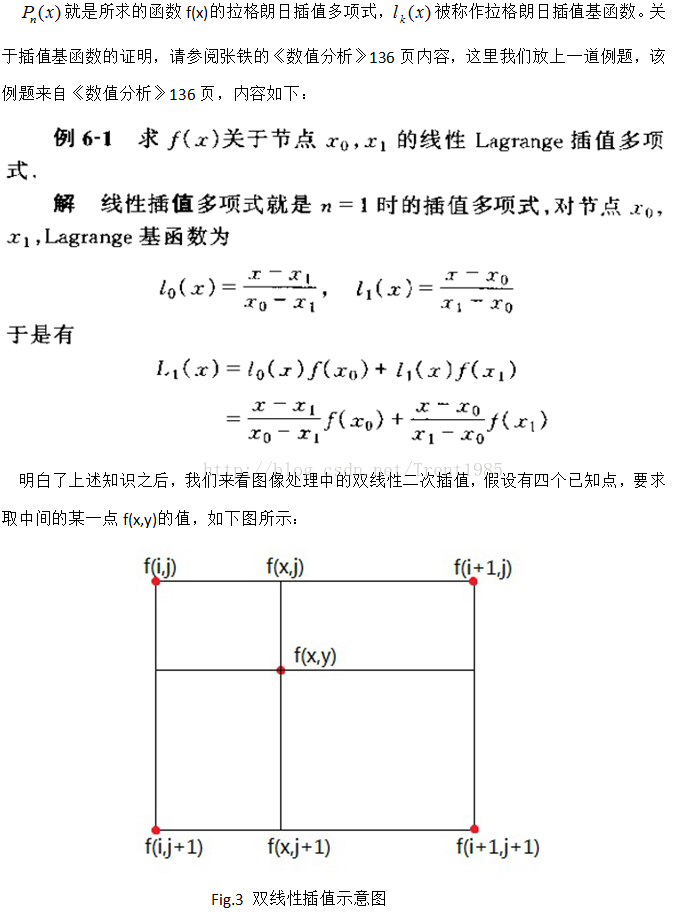
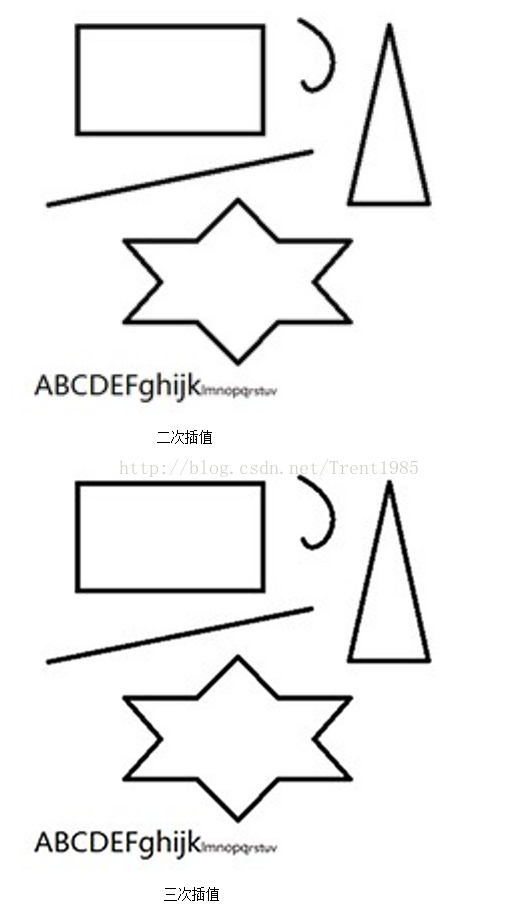
2，雙線性二次插值

    在介紹雙線性插值前，我們先介紹一下拉格朗日插值多項式。本文參考引用均來自

張鐵的《數值分析》一書。

 

  我們的方法是這樣的，根據水平方向上的雙線性二次插值，由f(I,j)和f(i+1,j)求取f(x,j)，由

f(I,j+1)和f(i+1,j+1)求取f(x,j+1)，然後再根據這兩點的二次插值求取f(x,y)。

  根據前面的例題，我們可以很容易的求取各點插值如下：

                        f(x,j)=(i+1-x)f(I,j)+(x-i)f(i+1,j)               公式1-(4)

                      f(x,j+1)=(i+1-x)f(I,j+1)+(x-i)f(i+1,j+1)           公式1-(5)

                       f(x,y)=(i+1-y)f(x,j)+(y-j)f(x,j+1)               公式1-(6)

  以上三式綜合可以得到：

  f(x,y)=(j+1-y)(i+1-x)f(I,j)+(j+1-y)(x-i)f(i+1,j)+(y-j)(i+1-x)f(I,j+1)+(y-j)(x-i)f(i+1,j+1)     公式1-(7)

  我們令x=i+p,y=j+q得：

  f(i+p,j+q)=(1-q)(1-p)f(I,j)+p(1-q)f(i+1,j)+q(1-p)f(I,j+1)+pqf(i+1,j+1)                公式1-(8)

  上式即為數字影象處理中的雙線性二次插值公式。

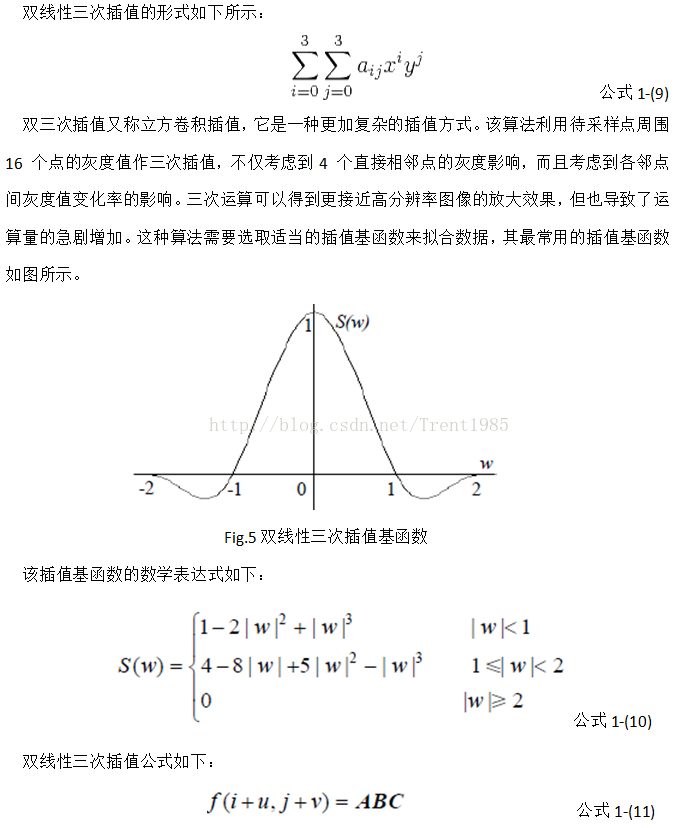
3，雙線性三次插值

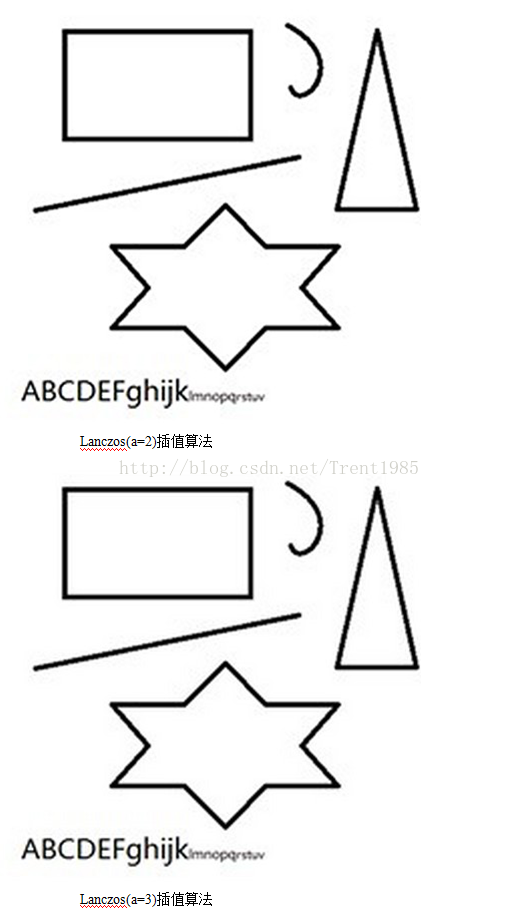
4，Lanczos插值演算法

這裡我大概介紹一下演算法的流程：

這個演算法也是一個模板演算法，主要內容是計算模板中的權重資訊。

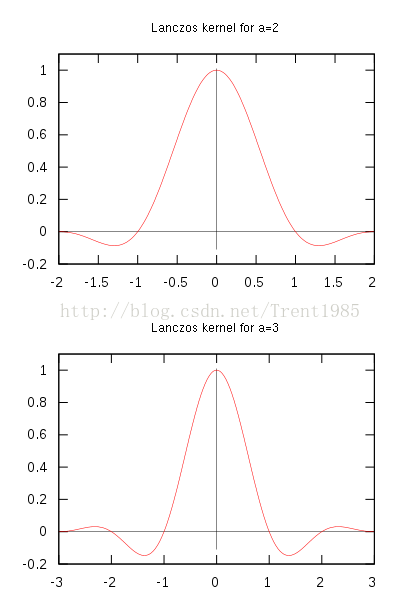
對於一維資訊，假如我們輸入點集為X，那麼，Lanczos對應有個視窗模板Window，這個視窗中每個位置的權重計算如下：

                         1-(12)

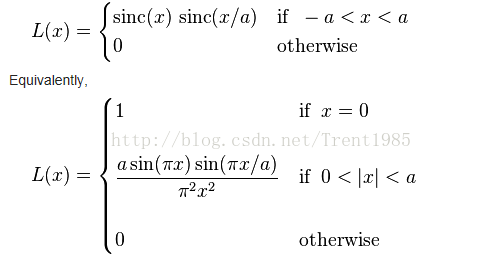
                 Fig.6 Lanczos

通常，這個a取2或者3，a=2時，該演算法適用於影象縮小插值；a=3時，該演算法適用於放大插值；對應不同a值得Lanczos插值曲線如上圖6所示；上述的公式分別為連續和離散的公式。我們根據輸入點X的位置，確定對應window中不同位置的權重L(x)，然後對模板中的點值取加權平均，公式如下：

                                                    1-(13)

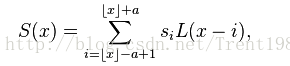
這個S(x)即為X處的插值結果。

根據上述一維插值，推廣得到多維插值公式如下(這裡以二維為例)：

 1-(14)

上述內容是對不同插值演算法簡單的進行了介紹，如果不明白可以查詢相關知識。

現在我們來看下相應的效果圖：

上面的一組效果圖均是先將原圖縮小50%，然後使用不同演算法放大到原圖大小得到的。由上面這組圖我們可以發現，效果最差的是最鄰近插值演算法，效果最好的是雙線性三次插值，Lanczos演算法跟三次插值大致一致；

由於程式語言不同，可能會造成耗時的差距，但是，對於同一種語言，統計得出：最鄰近插值速度最快，三次插值速度最慢，而Lanczos演算法與二次插值相仿。

綜上，Lanczos插值具有速度快，效果好，價效比最高的優點，這也是目前此演算法比較流行的原因。

最後，給出一個本人使用C#寫的Lanczos程式碼，程式碼未經優化，僅供測試，這裡的NP是對權重計算構建的對映表：

  1. private Bitmap ZoomLanczos2Apply(Bitmap srcBitmap, double k)  
  2.         {  
  3.             Bitmap src = new Bitmap(srcBitmap);  
  4.             int width = src.Width;  
  5.             int height = src.Height;  
  6.             BitmapData srcData = src.LockBits(new Rectangle(0, 0, width, height), ImageLockMode.ReadWrite, PixelFormat.Format32bppArgb);  
  7.             byte* pS = (byte*)srcData.Scan0;  
  8.             int w = (int)((double)width * k);  
  9.             int h = (int)((double)height * k);  
  10.             Bitmap dst = new Bitmap(w, h, PixelFormat.Format32bppArgb);  
  11.             BitmapData dstData = dst.LockBits(new Rectangle(0, 0, w, h), ImageLockMode.ReadWrite, PixelFormat.Format32bppArgb);  
  12.             byte* d = (byte*)dstData.Scan0;  
  13.             int offset = dstData.Stride - w * 4;  
  14.             int x = 0, y = 0;  
  15.             double p = 0, q = 0;  
  16.             double n1 = 0, n2 = 0, n3 = 0, n4 = 0, nSum = 0;  
  17.             int p0 = 0, p1 = 0, p2 = 0, p3 = 0, p4 = 0, gray = 0;  
  18.             byte* temp = null;  
  19.             double[] NP1 = new double[] { -0.00623896218505032, -0.0122238956025722, -0.0179556611741633, -0.0234353793884155, -0.028664425422539, -0.0336444239814841, -0.0383772438642046, -0.0428649922670393, -0.0471100088344975, -0.0511148594680326, -0.0548823299036605, -0.0584154190695433, -0.0617173322348938, -0.0647914739617815, -0.0676414408716196, -0.0702710142382982, -0.0726841524200902, -0.0748849831426012, -0.0768777956451566, -0.0786670327031274, -0.0802572825387739, -0.0816532706332581, -0.0828598514525135, -0.0838820000996894, -0.0847248039068906, -0.0853934539789171, -0.0858932367016755, -0.0862295252278804, -0.0864077709525887, -0.0864334949910196, -0.086312279671003, -0.0860497600522689, -0.0856516154846428, -0.0851235612170509, -0.0844713400690516, -0.0837007141764163, -0.0828174568220629, -0.0818273443634177, -0.0807361482670294, -0.0795496272610035, -0.0782735196155422, -0.0769135355615895, -0.0754753498572731, -0.0739645945115212, -0.0723868516738999, -0.0707476466993797, -0.0690524413963838, -0.0673066274661114, -0.0655155201407567, -0.0636843520278618, -0.0618182671676555, -0.0599223153098279, -0.0580014464157926, -0.0560605053920726, -0.0541042270600343, -0.0521372313667693, -0.0501640188415028, -0.048188966301476, -0.0462163228108206, -0.0442502058955092, -0.0422945980170336, -0.0403533433070252, -0.0384301445645995, -0.0365285605177724, -0.0346520033498648, -0.0328037364913793, -0.0309868726774121, -0.0292043722702325, -0.0274590418462525, -0.0257535330461864, -0.0240903416868009, -0.0224718071322479, -0.0209001119225812, -0.0193772816566703, -0.0179051851263444, -0.0164855346982315, -0.015119886939392, -0.013809643482501, -0.0125560521259855, -0.0113602081641975, -0.0102230559423803, -0.00914539063088284, -0.00812786021277406, -0.00717096767873418, -0.00627507342282205, -0.00544039783246632, -0.00466702406578012, -0.00395490100907222, -0.00330384640720963, -0.00271355015928674, -0.00218357777186753, -0.00171337396189679, -0.00130226640121749, -0.000949469594490465, -0.00065408888218426, -0.000415124560192089, -0.000231476107535702, -0.000101946513534946, -0 };  
  20.             double[] NP2 = new double[] { 0.999794398630316, 0.999177779156011, 0.998150695261436, 0.996714069021198, 0.994869189802256, 0.992617712728975, 0.989961656713271, 0.986903402052547, 0.983445687598761, 0.979591607502511, 0.975344607536654, 0.9707084810045, 0.965687364238256, 0.960285731693901, 0.954508390649264, 0.948360475512591, 0.941847441749449, 0.934975059436304, 0.927749406449645, 0.920176861299994, 0.912264095620641, 0.904018066321406, 0.895446007418168, 0.886555421549337, 0.877354071190877, 0.867849969581877, 0.858051371373022, 0.847966763010743, 0.83760485287009, 0.826974561149762, 0.816085009542993, 0.804945510698284, 0.793565557484247, 0.781954812073053, 0.770123094857198, 0.758080373214511, 0.745836750136481, 0.733402452735159, 0.720787820644003, 0.708003294328147, 0.695059403319663, 0.68196675439345, 0.668736019699406, 0.655377924866579, 0.641903237094975, 0.628322753250659, 0.614647287979759, 0.600887661856885, 0.587054689583387, 0.573159168250756, 0.559211865684328, 0.545223508882287, 0.531204772564777, 0.517166267847729, 0.503118531055783, 0.489072012688425, 0.47503706655321, 0.461023939079635, 0.447042758826945, 0.433103526198797, 0.419216103377392, 0.405390204489315, 0.391635386014941, 0.37796103745288, 0.364376372250524, 0.350890419011333, 0.33751201298905, 0.324249787878619, 0.311112167913061, 0.298107360275149, 0.285243347832182, 0.272527882201696, 0.259968477155437, 0.247572402368387, 0.235346677519141, 0.223298066747373, 0.211433073473617, 0.199757935586031, 0.188278620998268, 0.177000823582037, 0.165929959477376, 0.155071163783102, 0.144429287629353, 0.13400889563358, 0.123814263740785, 0.113849377448258, 0.104117930414501, 0.0946233234514916, 0.0853686638988765, 0.0763567653781721, 0.0675901479244855, 0.059071038492763, 0.050801371835042, 0.0427827917446759, 0.0350166526629909, 0.0275040216433488, 0.0202456806670952, 0.0132421293054104, 0.00649358772061002 };  
  21.             double[] NP3 = new double[] { 0.00649358772061002, 0.0132421293054104, 0.0202456806670952, 0.0275040216433488, 0.0350166526629909, 0.0427827917446759, 0.0508013718350421, 0.059071038492763, 0.0675901479244855, 0.0763567653781721, 0.0853686638988765, 0.0946233234514916, 0.104117930414501, 0.113849377448258, 0.123814263740785, 0.13400889563358, 0.144429287629353, 0.155071163783102, 0.165929959477376, 0.177000823582037, 0.188278620998268, 0.199757935586031, 0.211433073473617, 0.223298066747373, 0.235346677519141, 0.247572402368387, 0.259968477155437, 0.272527882201696, 0.285243347832182, 0.298107360275149, 0.311112167913061, 0.324249787878619, 0.33751201298905, 0.350890419011333, 0.364376372250524, 0.37796103745288, 0.391635386014941, 0.405390204489315, 0.419216103377392, 0.433103526198797, 0.447042758826944, 0.461023939079634, 0.475037066553209, 0.489072012688425, 0.503118531055783, 0.517166267847729, 0.531204772564777, 0.545223508882287, 0.559211865684328, 0.573159168250756, 0.587054689583387, 0.600887661856885, 0.614647287979759, 0.628322753250659, 0.641903237094975, 0.655377924866579, 0.668736019699406, 0.68196675439345, 0.695059403319663, 0.708003294328147, 0.720787820644003, 0.733402452735159, 0.745836750136481, 0.758080373214511, 0.770123094857198, 0.781954812073053, 0.793565557484247, 0.804945510698284, 0.816085009542993, 0.826974561149762, 0.837604852870089, 0.847966763010743, 0.858051371373022, 0.867849969581877, 0.877354071190877, 0.886555421549337, 0.895446007418168, 0.904018066321406, 0.912264095620641, 0.920176861299994, 0.927749406449646, 0.934975059436304, 0.941847441749449, 0.948360475512591, 0.954508390649264, 0.960285731693901, 0.965687364238256, 0.9707084810045, 0.975344607536654, 0.979591607502512, 0.983445687598761, 0.986903402052547, 0.989961656713271, 0.992617712728975, 0.994869189802256, 0.996714069021198, 0.998150695261436, 0.999177779156011, 0.999794398630316 };  
  22.             double[] NP4 = new double[] { -0, -0.000101946513534946, -0.000231476107535702, -0.000415124560192089, -0.00065408888218426, -0.000949469594490465, -0.0013022664012175, -0.00171337396189679, -0.00218357777186754, -0.00271355015928674, -0.00330384640720965, -0.00395490100907222, -0.00466702406578012, -0.00544039783246632, -0.00627507342282205, -0.00717096767873415, -0.00812786021277406, -0.00914539063088281, -0.0102230559423803, -0.0113602081641975, -0.0125560521259855, -0.013809643482501, -0.015119886939392, -0.0164855346982315, -0.0179051851263444, -0.0193772816566703, -0.0209001119225812, -0.0224718071322479, -0.0240903416868009, -0.0257535330461864, -0.0274590418462525, -0.0292043722702326, -0.0309868726774121, -0.0328037364913794, -0.0346520033498648, -0.0365285605177724, -0.0384301445645995, -0.0403533433070252, -0.0422945980170336, -0.0442502058955092, -0.0462163228108205, -0.048188966301476, -0.0501640188415028, -0.0521372313667693, -0.0541042270600343, -0.0560605053920726, -0.0580014464157926, -0.0599223153098279, -0.0618182671676555, -0.0636843520278618, -0.0655155201407567, -0.0673066274661114, -0.0690524413963838, -0.0707476466993797, -0.0723868516738999, -0.0739645945115212, -0.0754753498572731, -0.0769135355615895, -0.0782735196155421, -0.0795496272610035, -0.0807361482670294, -0.0818273443634177, -0.0828174568220629, -0.0837007141764163, -0.0844713400690516, -0.0851235612170509, -0.0856516154846428, -0.0860497600522689, -0.086312279671003, -0.0864334949910196, -0.0864077709525887, -0.0862295252278804, -0.0858932367016755, -0.0853934539789171, -0.0847248039068906, -0.0838820000996894, -0.0828598514525135, -0.0816532706332581, -0.0802572825387739, -0.0786670327031274, -0.0768777956451566, -0.0748849831426012, -0.0726841524200902, -0.0702710142382982, -0.0676414408716196, -0.0647914739617815, -0.0617173322348938, -0.0584154190695433, -0.0548823299036604, -0.0511148594680326, -0.0471100088344975, -0.0428649922670393, -0.0383772438642045, -0.0336444239814841, -0.028664425422539, -0.0234353793884155, -0.0179556611741633, -0.0122238956025722, -0.00623896218505032 };  
  23.             for (int j = 0; j < h; j++)  
  24.             {  
  25.                 q = (double)j / (double)k;  
  26.                 y = (int)q;  
  27.                 q = Math.Abs(q - (double)y);  
  28.                 p0 = y * srcData.Stride;  
  29.                 y = y >= height ? height - 1 : y;  
  30.                 for (int i = 0; i < w; i++)  
  31.                 {  
  32.                     p = (double)i / (double)k;  
  33.                     x = (int)p;  
  34.                     p = Math.Abs(p - (double)x);  
  35.                     temp = d + i * 4 + j * dstData.Stride;  
  36.                     if (p != 0)  
  37.                     {  
  38.                         x = (x >= width - 3 ? width - 3 : x);  
  39.                         x = x < 1 ? 1 : x;  
  40.                         gray = (int)(p * 100.0) - 1;  
  41.                         gray = Math.Max(0, gray);  
  42.                         n1 = NP1[gray];  
  43.                         n2 = NP2[gray];  
  44.                         n3 = NP3[gray];  
  45.                         n4 = 1.0 - n1 - n2 - n3;// NP4[gray];  
  46.                         p2 = x * 4 + p0;  
  47.                         p1 = p2 - 4;  
  48.                         p3 = p2 + 4;  
  49.                         p4 = p2 + 8;  
  50.                         nSum = n1 + n2 + n3 + n4;  
  51.                         gray = (int)((n1 * (double)((pS + p1)[0]) + n2 * (double)((pS + p2)[0]) + n3 * (double)((pS + p3)[0]) + n4 * (double)((pS + p4)[0])));  
  52.                         gray = Math.Max(0, Math.Min(255, gray));  
  53.                         temp[0] = (byte)gray;  
  54.                         gray = (int)((n1 * (double)((pS + p1)[1]) + n2 * (double)((pS + p2)[1]) + n3 * (double)((pS + p3)[1]) + n4 * (double)((pS + p4)[1])));  
  55.                         gray = Math.Max(0, Math.Min(255, gray));  
  56.                         temp[1] = (byte)gray;  
  57.                         gray = (int)((n1 * (double)((pS + p1)[2]) + n2 * (double)((pS + p2)[2]) + n3 * (double)((pS + p3)[2]) + n4 * (double)((pS + p4)[2])));  
  58.                         gray = Math.Max(0, Math.Min(255, gray));  
  59.                         temp[2] = (byte)gray;  
  60.                     }  
  61.                     else  
  62.                     {  
  63.                         x = x >= width ? width - 1 : x;  
  64.                         gray = x * 4 + y * srcData.Stride;  
  65.                         temp[0] = (byte)(pS + gray)[0];  
  66.                         temp[1] = (byte)(pS + gray)[1];  
  67.                         temp[2] = (byte)(pS + gray)[2];  
  68.                     }  
  69.                     temp[3] = (byte)255;  
  70.                 }  
  71.             }  
  72.             for (int i = 0; i < w; i++)  
  73.             {  
  74.                 p = (double)i / (double)k;  
  75.                 x = (int)p;  
  76.                 p = Math.Abs(p - (double)x);  
  77.                 x = x >= width ? width - 1 : x;  
  78.                 for (int j = 0; j < h; j++)  
  79.                 {  
  80.                     q = (double)j / (double)k;  
  81.                     y = (int)q;  
  82.                     q = Math.Abs(q - (double)y);  
  83.                     p0 = y * srcData.Stride;  
  84.                     temp = d + i * 4 + j * dstData.Stride;  
  85.                     if (q != 0)  
  86.                     {  
  87.                         y = y >= height - 3 ? height - 3 : y;  
  88.                         y = y < 1 ? 1 : y;  
  89.                         gray = (int)(q * 100.0) - 1;  
  90.                         gray = Math.Max(0, gray);  
  91.                         n1 = NP1[gray];  
  92.                         n2 = NP2[gray];  
  93.                         n3 = NP3[gray];  
  94.                         n4 = 1.0 - n1 - n2 - n3;// NP4[gray];  
  95.                         nSum = n1 + n2 + n3 + n4;  
  96.                         p2 = x * 4 + y * srcData.Stride;  
  97.                         p1 = p2 - srcData.Stride;  
  98.                         p3 = p2 + srcData.Stride;  
  99.                         p4 = p3 + srcData.Stride;  
  100.                         gray = (int)((n1 * (double)((pS + p1)[0]) + n2 * (double)((pS + p2)[0]) + n3 * (double)((pS + p3)[0]) + n4 * (double)((pS + p4)[0])));  
  101.                         gray = Math.Max(0, Math.Min(255, gray));  
  102.                         temp[0] = (byte)gray;  
  103.                         gray = (int)((n1 * (double)((pS + p1)[1]) + n2 * (double)((pS + p2)[1]) + n3 * (double)((pS + p3)[1]) + n4 * (double)((pS + p4)[1])));  
  104.                         gray = Math.Max(0, Math.Min(255, gray));  
  105.                         temp[1] = (byte)gray;  
  106.                         gray = (int)((n1 * (double)((pS + p1)[2]) + n2 * (double)((pS + p2)[2]) + n3 * (double)((pS + p3)[2]) + n4 * (double)((pS + p4)[2])));  
  107.                         gray = Math.Max(0, Math.Min(255, gray));  
  108.                         temp[2] = (byte)gray;  
  109.                     }  
  110.                     else  
  111.                     {  
  112.                         y = y >= height ? height - 1 : y;  
  113.                         gray = x * 4 + y * srcData.Stride;  
  114.                         temp[0] = (byte)(pS + gray)[0];  
  115.                         temp[1] = (byte)(pS + gray)[1];  
  116.                         temp[2] = (byte)(pS + gray)[2];  
  117.                     }  
  118.                     temp[3] = (byte)255;  
  119.                 }  
  120.             }  
  121.             src.UnlockBits(srcData);  
  122.             dst.UnlockBits(dstData);  
  123.             return dst;  
  124.         }  

最後，分享一個專業的影象處理網站（微畫素），裡面有很多原始碼下載： http://www.zealpixel.com/portal.php

相關推薦

Lanczos插值，最鄰近插值，雙線性二次插值，三次插值

本文為轉載，原部落格地址：http://blog.csdn.net/trent1985/article/details/45150677 [研究內容] 目前比較常用的幾種插值演算法 [正文] 目前比較常用的插值演算法有這麼幾種：最鄰近插值，雙線性二次插值，三次插值， Lan

雙線性插值法，最鄰近法 處理圖片的旋轉，放大

對於一張圖片旋轉某個角度，其實就是把每個畫素計算好它的位置，再對對應的位置設定畫素值即可，以順時針為例，如下圖，由P點旋轉到P'， x=rcos(a) y=rsin(a) x'=rcos(a+b)=rcos(a)cos(b)-rsin(a)sin(b) y'=rsi

影象處理中兩種基本的插值演算法(最鄰近插值法和雙線性內插法)

在影象的基本仿射變換中，經常會碰到經過旋轉、縮放後灰度值如何賦值的問題。因為變換之後，影象的座標位置有可能是小數，所以就需要插值演算法來確定到底將該畫素賦予哪個位置。 1、最鄰近插值法(Nearest Interpolation) 這是最簡單的一種插值方法，不需要計算。在待

雙線性二次插值原理解析

對某個多項式函式，已知有給定的k + 1個取值點： 其中對應著自變數的位置，而對應著函式在這個位置的取值。 假設任意兩個不同的xj都互不相同，那麼應用拉格朗日插值公式所得到的拉格朗日插值多項式為： 其中每個為拉格朗日基本多項式（或稱插值基函式），其表示式為： [3]拉格朗日基本多項式的特點是在上取值為

定義一個數組，陣列初始長度由控制檯獲取 。隨後手動給陣列中每個元素賦值，陣列滿後將陣列長度擴充二倍並輸出，清空陣列中所有元素且值繼承陣列長度，並重新進行手動新增元素，無限死迴圈直至輸出-0後結束程式。

package com.tedu; import java.util.Arrays; import java.util.Scanner; /** * 需求: * 定義一個初始陣列，陣列初始長度由控制檯獲取 * 隨後手動給陣列中每個元素賦值，陣列滿後將陣列長度擴充二倍輸

maven專案的JDK版本的版本配置或者指定JDK版本，最實用的修改settings.xml和pom.xml修改方法，可以解決eplise中的90%因為jdk相容的問題，

公司近期匯入了一個專案，新專案剛剛匯入就有很多錯誤，這也是java專案的一個通病，根本的原因還是java的jvm虛擬機器的問題，還有各種依賴包的問題，有些問題很明顯，有些問題非常不明顯 下面我就把一些應為jdk版本引起的問題記錄下， 錯誤1：Dynamic We

影象演算法（一）：最近鄰插值，雙線性插值，三次插值

最近在複習影象演算法，對於一些簡單的影象演算法進行一個程式碼實現，由於找工作比較忙，具體原理後期補上，先上程式碼。今天先給出最近鄰插值，雙線性插值，三次插值。 1.最近鄰插值 原始圖中影響點數為1 （1）程式碼 # include<iostream>

最鄰近插值法(The nearest interpolation)實現影象縮放

也稱零階插值。它輸出的畫素灰度值就等於距離它對映到的位置最近的輸入畫素的灰度值。但當影象中包含畫素之間灰度級有變化的細微結構時,最鄰近演算法會在影象中產生人為加工的痕跡。 具體計算方法：對於一個目的座標

Matlab 插值演算法（最鄰近、雙線性、雙三次插值）

1、最鄰近元法 這是最簡單的一種插值方法，不需要計算，在待求象素的四鄰象素中，將距離待求象素最近的鄰象素灰度賦給待求象素。設i+u, j+v(i, j為正整數， u, v為大於零小於1的小數，下同)為待求象素座標，則待求象素灰度的值 f(i+u, j+v) 如下圖所示：

影象演算法的基礎知識(雙線性插值，協方差矩陣，矩陣的特徵值、特徵向量）

0. 前言 MATLAB或者OpenCV裡有很多封裝好的函式，我們可以使用一行程式碼直接呼叫並得到處理結果。然而當問到具體是怎麼實現的時候，卻總是一臉懵逼，答不上來。前兩天參加一個演算法工程師的筆試題，其中就考到了這幾點，感到非常汗顏！趕緊補習！ 1. 雙線性插值 在影象處

最近鄰插值和雙線性插值的基本原理 以及OpenCV中resize函式的用法改變影象的大小

最近鄰插值和雙線性插值的基本原理 影象的縮放很好理解,就是影象的放大和縮小。傳統的繪畫工具中,有一種叫做“放大尺”的繪畫工具，畫家常用它來放大圖畫。當然，在計算機上，我們不再需要用放大尺去放大或縮小影象了，把這個工作交給程式來完成就可以了。下面就來講講計算機怎麼來放大縮小圖象；在本文中，

線性插值，雙線性插值Bilinear Interpolation演算法

線性插值 先講一下線性插值：已知資料 (x0, y0) 與 (x1, y1)，要計算 [x0, x1] 區間內某一位置 x 在直線上的y值（反過來也是一樣，略）： y−y0x−x0=y1−y0x1−x0y−y0

最臨近 雙線性 三次卷積插值（影象放縮）

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

影象演算法-最近鄰插值 雙線性插值

影象插值演算法包括向上插值和向下插值，向上插值就是對影象進行放大，向下插值就是對影象進行縮小，插值演算法在影象預處理過程中經常被使用，通過插值演算法，可以將影象尺寸變換為任意尺寸，下面以舉例子的方式來說明兩種常見的插值演算法： 假設影象原始尺寸為wi,hi，縮

最臨近插值和雙線性內插值演算法實現比較

影象縮放顧名思義，就是把原影象按照目標尺寸放大或者縮小，是影象處理的一種。自然，影象縮放的核心也就是怎麼樣根據已知影象計算目標影象的各點畫素值。最簡單的是最臨近插值演算法，這種演算法就是根據原影象和目標影象的尺寸，計算縮放的比例，然後根據縮放比例計算目標畫素所依據的原畫素，過

影象放縮中最近鄰插值和雙線性插值的基本原理

影象的縮放很好理解,就是影象的放大和縮小。傳統的繪畫工具中,有一種叫做“放大尺”的繪畫工具，畫家常用它來放大圖畫。當然，在計算機上，我們不再需要用放大尺去放大或縮小影象了，把這個工作交給程式來完成就可以了。下面就來講講計算機怎麼來放大縮小圖象；在本文中，我們所說的影象都是指

最臨近、雙線性、三次卷積插值演算法比較

 //原文：http://blog.csdn.net/google0802/article/details/8938849 【我只是想把最近鄰這個弄過來╮(╯-╰)╭ 】 插值演算法對於縮放比例較小的情況是完全可以接受的，令人信服的。一般的，縮小0.5倍以上或放大3.

插值---雙線性，三線性，四線性 及非線性

網上有很多這方面的資料，介紹的也算明白。但是，這些文章只介紹了演算法，並沒有具體說怎麼實現以及怎麼實現最好，舉個例子，你可以按照網上文章的演算法自己寫一個雙線性插值程式，用它對一張圖片進行處理，然後再用matlab或者openCV的resize函式對同一張圖片進行處理，得到的結果是不一樣的，如果源圖片較小

最近鄰、雙線性、三次卷積插值

轉載最鄰近插值（近鄰取樣法）：　　最臨近插值的的思想很簡單。對於通過反向變換得到的的一個浮點座標，對其進行簡單的取整，得到一個整數型座標，這個整數型座標對應的畫素值就是目的畫素的畫素值，也就是說，取浮點座標最鄰近的左上角點（對於DIB是右上角，因為它的掃描行是逆序儲存的）對應

最近鄰內插值與雙線性插值

前一陣想改進個影象處理的演算法，發現基礎太差了，還是要從基礎開始，畢竟一口出不成胖子 於是自己學習一下影象處理的基本知識。看到兩個最簡單的演算法 一個是最近鄰內插值和雙線性插值，決定自己實現以下，順便也能瞭解一下數字影象內部的儲存結構。 以下為簡單整理 by the way