問題
給定平面上N個點的座標，找出距離最遠的兩個點。
分析
類似於“最近點對問題”，這個問題也可以用列舉的方法求解，時間複雜度O(n^2)。
“尋找最近點對”是用到分治策略降低複雜度，而“尋找最遠點對”可利用幾何性質。注意到：對於平面上有n個點，這一對最遠點必然存在於這n個點所構成的一個凸包上（證明略），那麼可以排除大量點，如下圖所示：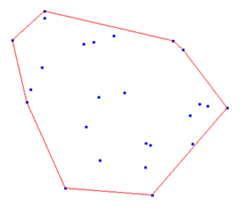

在得到凸包以後，可以只在頂點上面找最遠點了。同樣，如果不O(n^2)兩兩列舉，可以想象有兩條平行線， “卡”住這個凸包，然後卡緊的情況下旋轉一圈，肯定就能找到凸包直徑，也就找到了最遠的點對。或許這就是為啥叫“旋轉卡殼法”。

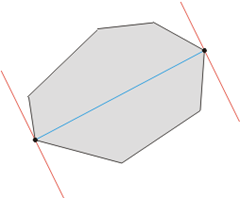
總結起來，問題解決步驟為：
1、用Graham's Scanning求凸包
2、用Rotating Calipers求凸包直徑，也就找到了最遠點對。
該演算法的平均複雜度為O(nlogn) 。最壞的情況下，如果這n個點本身就構成了一個凸包，時間複雜度為O(n^2)。

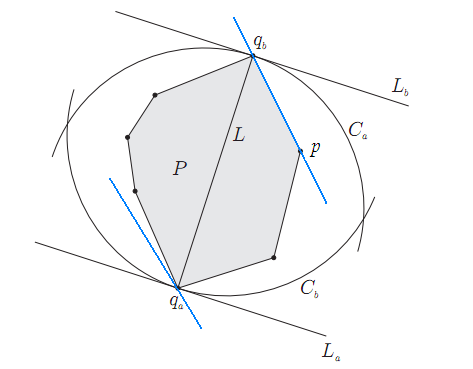
逆向思考，如果qa，qb是凸包上最遠兩點，必然可以分別過qa，qb畫出一對平行線。通過旋轉這對平行線，我們可以讓它和凸包上的一條邊重合,如圖中藍色直線，可以注意到，qa是凸包上離p和qb所在直線最遠的點。於是我們的思路就是列舉凸包上的所有邊，對每一條邊找出凸包上離該邊最遠的頂點，計算這個頂點到該邊兩個端點的距離，並記錄最大的值。直觀上這是一個O(n2)的演算法，和直接列舉任意兩個頂點一樣了。但是注意到當我們逆時針列舉邊的時候，最遠點的變化也是逆時針的，這樣就可以不用從頭計算最遠點，而可以緊接著上一次的最遠點繼續計算，於是我們得到了O(n)的演算法。

1. // 求最遠點對
2. #include<iostream>
3. #include<algorithm>
4. usingnamespace std;  
5. struct point  
6. {  
7.     int x , y;  
8. }p[50005];  
9. int top , stack[50005];    // 凸包的點存在於stack[]中
10. inlinedouble dis(const point &a , const point &b)  
11. {  
12.     return (a.x - b.x)*(a.x - b.x)+(a.y - b.y)*(a.y - b.y);  
13. }  
14. inlineint max(int a , int b)  
15. {  
16.     return a > b ? a : b;  
17. }  
18. inlineint xmult(const point &p1 , const point &p2 , const point &p0)  
19. {   //計算叉乘--線段旋轉方向和對應的四邊形的面積--返回(p1-p0)*(p2-p0)叉積
20.     //if叉積為正--p0p1在p0p2的順時針方向; if(x==0)共線
21.     return (p1.x-p0.x)*(p2.y-p0.y) - (p1.y-p0.y)*(p2.x-p0.x);  
22. }  
23. int cmp(constvoid * a , constvoid * b) //逆時針排序 返回正數要交換
24. {  
25.     struct point *p1 = (struct point *)a;  
26.     struct point *p2 = (struct point *)b;  
27.     int ans = xmult(*p1 , *p2 , p[0]);   //向量叉乘
28.     if(ans < 0)   //p0p1線段在p0p2線段的上方，需要交換
29.         return 1;  
30.     elseif(ans == 0 && ( (*p1).x >= (*p2).x))     //斜率相等時，距離近的點在先
31.         return 1;  
32.     else
33.         return -1;  
34. }  
35. void graham(int n) //形成凸包
36. {  
37.     qsort(p+1 , n-1 , sizeof(point) , cmp);  
38.     int i;  
39.     stack[0] = 0 , stack[1] = 1;  
40.     top = 1;  
41.     for(i = 2 ; i < n ; ++i)  
42.     {  
43.         while(top > 0 && xmult( p[stack[top]] , p[i] , p[stack[top-1]]) <= 0)  
44.             top--;           //順時針方向--刪除棧頂元素
45.         stack[++top] = i;    //新元素入棧
46.     }  
47.     int temp = top;  
48.     for(i = n-2 ; i >= 0 ; --i)  
49.     {  
50.         while(top > temp && xmult(p[stack[top]] , p[i] , p[stack[top-1]]) <= 0)  
51.             top--;  
52.         stack[++top] = i;    //新元素入棧
53.     }  
54. }  
55. int rotating_calipers()  //卡殼
56. {  
57.     int i , q=1;  
58.     int ans = 0;  
59.     stack[top]=0;  
60.     for(i = 0 ; i < top ; i++)  
61.     {  
62.         while( xmult( p[stack[i+1]] , p[stack[q+1]] , p[stack[i]] ) > xmult( p[stack[i+1]] , p[stack[q]] , p[stack[i]] ) )  
63.             q = (q+1)%(top);  
64.         ans = max(ans , max( dis(p[stack[i]] , p[stack[q]]) , dis(p[stack[i+1]] , p[stack[q+1]])));  
65.     }  
66.     return ans;  
67. }  
68. int main(void)  
69. {  
70.     int i , n , leftdown;   
71.     while(scanf("%d",&n) != EOF)  
72.     {  
73.         leftdown = 0;  
74.         for(i = 0 ; i < n ; ++i)  
75.         {  
76.             scanf("%d %d",&p[i].x,&p[i].y);  
77.             if(p[i].y < p[leftdown].y || (p[i].y == p[leftdown].y && p[i].x < p[leftdown].x))  //找到最左下角的點
78.                 leftdown = i;  
79.         }  
80.         swap(p[0] , p[leftdown]);  
81.         graham(n);  
82.         printf("%d\n",rotating_calipers());    
83.     }  
84.     return 0;  
85. }