Bresenham是繪製線段最有效率的演算法之一,該演算法僅僅使用整型加減及位元組位操作運算 (省去了用於計算斜率的除法運算)，因而計算效率非常高。其實現也非常的簡單明瞭。本文以Java程式碼為例，一步一步由淺而深的講解了Bresenham演算法的完整實現。

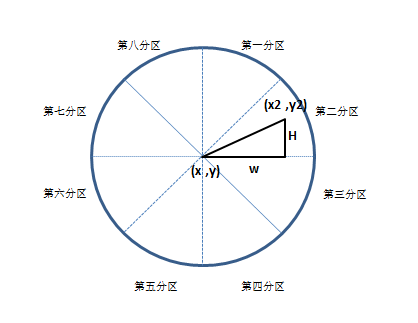
下圖所示，二維座標系統可均分為八個分割槽，作為本文例子的線段（x，y，x2，y2）位於第二分割槽。

在實現該演算法之前，我們先看看最原始，最直觀的做法。該原始演算法可以幫助更好的闡述布氏演算法，因為布氏演算法本身就是該原始演算法的擴充套件和優化。

    public void drawLineRaw(int x, int
 
 y, int x2, int y2, int color) {
        int w = x2 - x;
        int h = y2 - y;
        double m = h / (double) w;
        double j = y;
        for (int i = x; i <= x2; i++) {
            drawPixel(i, (int) j, color);
            j += m;
        }
    }

該實現儘管效率低，但實現了我們需要的功能。注意！上面程式碼實際只能畫位於第二分割槽的線條，而不能畫位於其它分割槽的線條。當耐心讀完本文，在結尾部分我們會看到覆蓋所有分割槽的完整的實現。

操作m = h / w，j + = m實際上是增加了分子，並保持分母不變。當分子h變得等於或大於分母w，分子減去分母並將j增加1（實現該操作對應的程式碼為(int) j）。 這闡述了Bresenham演算法的基本原理，Bresenham演算法用整數加法取代了除法和實數操作。如下程式碼為Bresenham演算法在第二分割槽的實現。(該部分是理解全文的關鍵，請仔細體會)

      public void drawIn2ndOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int
 
 h = y2 - y;
              int dy1 = -1;
              int fastStep = Math.abs(w);
              int slowStep =Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x++;
              }
       }

注意， int numerator = fastStep >> 1; 分子等於快速變數的一半，該步驟讓y值的四捨五入在中間點而不是在整數點。

一個完整的畫線功能將需要考慮所有的分割槽， 那我們是否需要8份如上所示的程式碼呢？答案是不，其它八個分割槽的實現都十分相似，並很容易通用化。首先，我們來看看在不同的八分割槽的相似之處。 在第三分割槽線段只是第二分割槽線段基於Y方向的映象，因此只需設定dy1 = 1，而不是dy1=-1。請參見下面的第4行的區別。

       public void drawIn3rdOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = 1;
              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x++;
              }
       }

在第六分割槽和第三分割槽的實現是基本相同的，除了基於座標軸的映象。這可以通過改變程式碼 x++為x- - ​​來實現。 簡單吧！

       public void drawIn6thOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = 1;
              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x--;
              }
       }

這同樣適用於第七分割槽與第二分割槽。可以通過改變行x ++為x–​​來實現。

    public void drawIn7thOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = -1;
              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x--;
              }
        }

重複，重複… 重構！如下是一個通用於第二，第三，第六和第七分割槽的線段繪製功能。

    public void drawInEvenOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dx1 = w < 0 ? -1: (w > 0 ? 1 : 0);
              int dy1 = h < 0 ? -1: (h > 0 ? 1 : 0);
              int dx2 = 0;
              int dy2 = dx2 = w < 0? -1 : (w > 0 ? 1 : 0);

              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           x+= dx1;
                           y+= dy1;
                     }else {
                           x+= dx2;
                           y+= dy2;
                     }
              }
       }

到目前為止，我們實現的第二，第三，第六,第七分割槽的畫線功能。然而，這仍然不完整。我們發現位於第一，第四，第五，和第八分割槽具有一個共同的區別，其高度的變化快於寬度的變化，而在第二，第三，第六，和第七分割槽的線段，其寬度的變化快於高度的變化。綜合該邏輯，如下是Bresenham演算法的對所有的八分割槽畫線的完整實現。

      public void drawLine(int x0,int y0,int x1,int y1,int color) {
              int x = x0;
              int y = y0;

              int w = x1 - x0;
              int h = y1 - y0;

              int dx1 = w < 0 ? -1: (w > 0 ? 1 : 0);
              int dy1 = h < 0 ? -1: (h > 0 ? 1 : 0);

              int dx2 = w < 0 ? -1: (w > 0 ? 1 : 0);
              int dy2 = 0;

              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              if (fastStep <=slowStep) {
                     fastStep= Math.abs(h);
                     slowStep= Math.abs(w);

                     dx2= 0;
                     dy2= h < 0 ? -1 : (h > 0 ? 1 : 0);
              } 
              int numerator = fastStep>> 1;

              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (numerator >=fastStep) {
                           numerator-= fastStep;
                           x+= dx1;
                           y+= dy1;
                     }else {
                           x+= dx2;
                           y+= dy2;
                     }
              }
       }