2. 程式人生 > >高斯分佈補充知識

高斯分佈補充知識

阿新 • • 發佈：2019-01-31

PRML第二章啃到高斯分佈的時候就開始不知所云了，看了這篇BlogPRML Chapter 2.3 The Gaussian Distribution之後，覺得講的很清晰，可惜作者沒有寫完，於是轉過去看了“Methods of Multivariate Analysis ”的第三章。這裡是對這些基礎知識點的一個記錄，用來日後複習。

單變數和雙變數

單變數的均值和方差

變數y的n個觀察量y 1 ,y 2 ,y 3 ,...,y n  ，那麼樣本均值：

y ¯ =1n∑ i=1 n y i  
樣本均值y ¯  永遠不會等於變數y的總體均值μ ，儘管隨著樣本數量的增加y ¯  會無限接近μ
 。y ¯  是μ 的無偏估計量，因為E(y ¯ )=μ,var(y ¯ )=σ 2 n 
樣本方差：s 2 =∑ n i=1 (y i −y ¯ )n−1 
同理s 2  是總體方差σ 2  的無偏估計量

雙變數的協方差和相關性

協方差

協方差表示兩個變數之間的關係，下圖中是一些身高和體重的樣本資料
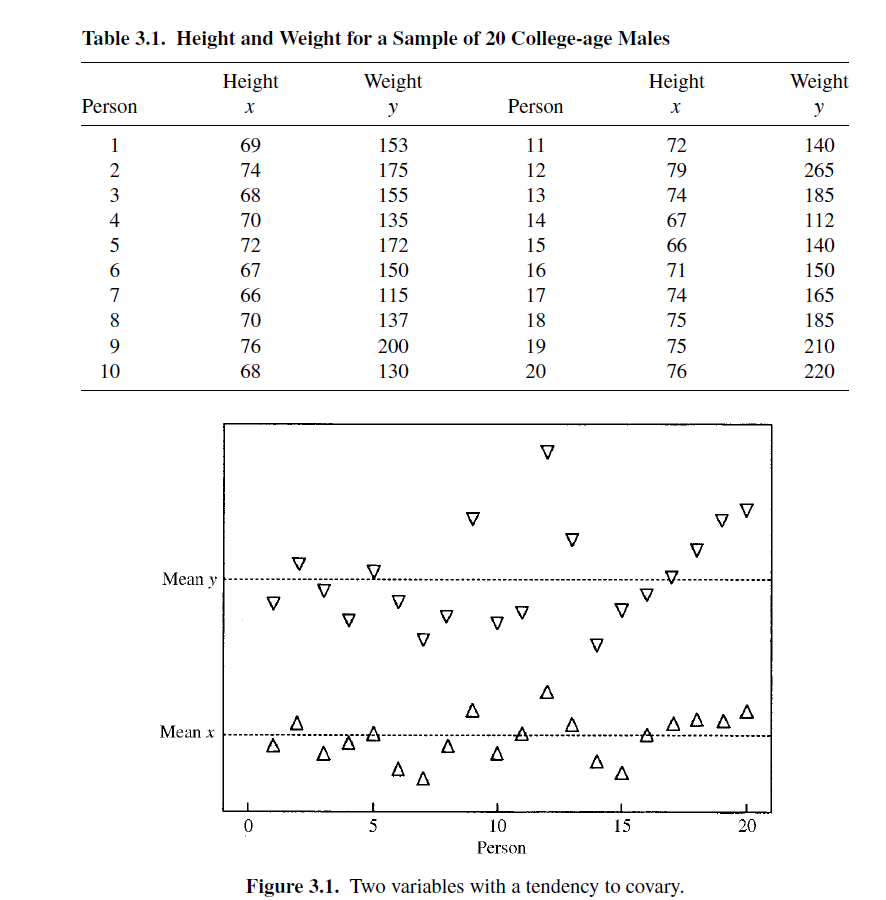
這裡寫圖片描述
如果把樣本用下邊的圖表示出來，可以發現當身高高於平均值的時候往往體重也會高於平均值，這兩者之間可能存在一些相關
兩個隨機變數x和y之間的關係：

E(x+y)=E(x)+E(y) 
E(xy)=E(x)E(y)x和y相互獨立 
如果變數x和y的聯合概率密度可以表示為p
(x,y)=p(x)p(y) 那麼變數x和y相互獨立，二者相互獨立也就是彼此不會相互影響
如果x和y相互獨立，那麼二者的協方差σ xy =0 ；反之，如果x,y的協方差σ xy =0 則不能說明二者相互獨立
σ xy =E(xy)−μ x μ y =E(x)E(y)−μ x μ y −μ x μ y =μ x μ y −μ x μ y =0 
樣本協方差：
s xy =∑ n i=1 (x i −x ¯ )(y i −y ¯ )n−1 
s xy =∑ n i=1 x i y i −nx ¯ y ¯ n−1 
s xy  永遠也不會等於σ xy  ，前者是後者的無偏估計量
樣本協方差矩陣只衡量二者之間的線性關係

兩組樣本的樣本協方差為0表示這兩組樣本正交

相關性

從上邊可以看出，如果把變數x和y的樣本同時乘以一個係數，那麼二者的協方差也會發生變化，由此可以看出協方差與尺度相關，於是引入總體相關性：

ρ=corr(x,y)=σ xy σ x σ y =

相關推薦

高斯分佈補充知識

PRML第二章啃到高斯分佈的時候就開始不知所云了，看了這篇BlogPRML Chapter 2.3 The Gaussian Distribution之後，覺得講的很清晰，可惜作者沒有寫完，於是轉過去看了“Methods of Multivariate Anal

高斯分佈 協方差

高斯分佈（Gaussian Distribution）的概率密度函式（probability density function）： 對應於numpy中： numpy.random.normal(loc=0.0, scale=1.0, size=None) 引數的意義為： loc：flo

python 多維高斯分佈資料生成

import numpy as np import matplotlib.pyplot as plt def gen_clusters(): mean1 = [0,0] cov1 = [[1,0],[0,10]] data = np.random.multi

【學習筆記】Pattern Recognition&Machine Learning [1.2] Probability Theory(2) 基於高斯分佈和貝葉斯理論的曲線擬合

    高斯分佈不必贅述，這裡記錄個有意思的東西，即從高斯分佈和貝葉斯理論出發看曲線擬合（即選擇引數w）。     首先假設我們使用多項式擬合曲線，根據泰勒展開的方法，我們可以用有限項多項式在一定精度內擬合任何曲線。  &nb

機器學習儲備（2）：高斯分佈

今天講解獨立同分布的概念，高斯分佈，一維高斯分佈。 1、獨立同分布 指隨機過程中，任何時刻的取值都為隨機變數，如果這些隨機變數服從同一分佈，並且互相獨立，那麼這些隨機變數是獨立同分布。 先說說獨立這個概念。在預測德克薩斯州區域的房屋價值時，房屋樣本x1和樣本x2之間的預測是相互獨立的，它

廣義高斯分佈（GGD）

廣義高斯分佈（GGD）-Generalized Gaussian Distribution  廣義高斯分佈及其在影象去噪的應用_百度文庫 https://wenku.baidu.com/view/2b86384c852458fb770b5651.html     &n

到現在才理解高斯分佈的均值與方差為什麼是0和1

問題的來源，如圖所示：為什麼標準正態分佈的期望值0，方差為1呢，如果是針對x變數，期望值為0可以理解，那麼方差為1怎麼理解呢，顯然不可能為1，如果針對y變數，顯然所有值都大於0，怎麼會期望值會大於0呢： 先看數學期望的定義： 期望值本身是對所有值進行加權的過程，是針對一個變數存在的；每

概率分佈---高斯分佈

條件高斯分佈 邊緣高斯分佈 高斯變數的貝葉斯定理 高斯分佈的最大似然估計 順序估計 高斯分佈的貝葉斯推斷 學生t

多元高斯分佈

多元高斯分佈 1.協方差矩陣 協方差衡量的是變數X與Y之間是否存線上性關係，cov(X,Y)>0說明X與Y的變化趨勢是一致的，X增長的時候Y也隨著增長。如果X，Y互相獨立的話，cov(X,Y)=0. cov(X,X)=D(X)，變數X與自身的協方差就是方差，cov(X,Y)=cov

多元高斯分佈的KL散度

kl散度意義： In the context of machine learning, is often called the information gain achieved if Q is used instead of P. This reflects

opencv學習（十）：高斯模糊理論知識

理論知識： 參考連結： 對Photoshop高斯模糊濾鏡的演算法總結：http://www.cnblogs.com/hoodlum1980/archive/2008/03/03/1088567.html Python計算機視覺3：模糊,平滑,去噪：https://www.cnblogs.

伯努利分佈和高斯分佈下的最大似然估計

最大似然估計： 由於每一個樣本是否出現都對應著一定的概率，而且一般來說這些樣本的出現都不那麼偶然，因此我們希望這個概率分佈的引數能夠以最高的概率產生這些樣本。如果觀察到的資料為D1 , D2 , D3 ，…， DN ，那麼極大似然的目標如下： 通常上面這個概率的計算並不容易。

伯努利分佈、二項分佈、多項分佈、貝塔分佈、狄利克雷分佈、高斯分佈

伯努利分佈： 伯努利分佈(Bernoulli distribution)又名兩點分佈或0-1分佈，介紹伯努利分佈前首先需要引入伯努利試驗（Bernoulli trial）。 伯努利試驗是隻有兩種可能結果的單次隨機試驗，即對於一個隨機變數X而言： 伯努利試驗都可以表達為“是或否”

Stanford機器學習-異常檢測和多元高斯分佈

一、異常檢測 這章主要學習異常檢測問題，它是機器演算法的一個常見應用，同時也對於我們生活中的很多問題有很大的幫助，總的來說，它主要用於非監督的學習問題。 那我們怎麼來理解異常檢測是一個怎麼樣的問題呢？我們來看一個相關的問題：飛機引擎的檢測。因為引擎對於飛機來說

python畫高斯分佈圖形

高斯分佈，也叫正態分佈，是一個在數學、物理及工程等領域都非常重要的概率分佈，在統計學的許多方面有著重大的影響力。 若隨機變數X服從一個數學期望為μ、方差為σ^2的正態分佈，記為N(μ，σ^2)。其概率密度函式為正態分佈的期望值μ決定了其位置，其標準差σ決定了分佈的寬度。當μ = 0,σ = 1時的正態分佈是

C++ 產生均勻分佈 高斯分佈 函式

class Sample { public: static int uniform(int from, int to); static double uniform(); static double gaussian(double sigma); }; static double

菜鳥學概率統計——高斯分佈

正態分佈是最重要的一種概率分佈。正態分佈概念是由德國的數學家和天文學家Moivre於1733年首次提出的，但由於德國數學家Gauss率先將其應用於天文學家研究，故正態分佈又叫高斯分佈，高斯這項工作對後世的影響極大，他使正態分佈同時有了“高斯分佈”的名稱，後世之所以多將最小二乘法的發明權歸之於他，也是出於這一工

MKL/VSL，vRngGaussian：生成高斯分佈隨機數

以產生Gauss分佈隨機數為例，需要的步驟有： 1. 定義type(vsl_stream_state) :: stream。 按照手冊，stream的定義為“Random stream (or stream) is an abstract source

二維高斯分佈（Two-dimensional Gaussian distribution）的引數分析

　　最近在看高斯混合模型（Gaussian Mixture Model, GMM），涉及到高斯分佈的引數。為此特意回顧了概率論的二維高斯分佈的相關概念，並分析了引數對二維高斯分佈曲面的影響。 1、多維高斯分佈的概率密度函式 　　　 　　多維變數X

正態分佈（Normal distribution）與高斯分佈（Gaussian distribution）

正態分佈（Normal distribution）又名高斯分佈（Gaussian distribution），是一個在數學、物理及工程等領域都非常重要的概率分佈，在統計學的許多方面有著重大的影響力。 若隨機變數X服從一個數學期望為μ、標準方差為σ2的高斯分佈，記為： X