多元高斯分佈的KL散度
kl散度意義:
-
In the context of machine learning,
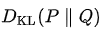
is often called the information gain achieved if Q is used instead of P. -
This reflects the asymmetry in Bayesian inference, which starts from a prior Q and updates to the posterior P.
-
公式:
證明:https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians
相關推薦
多元高斯分佈的KL散度
kl散度意義: In the context of machine learning, is often called the information gain achieved if Q is used instead of P. This reflects
多元高斯分佈
多元高斯分佈 1.協方差矩陣 協方差衡量的是變數X與Y之間是否存線上性關係,cov(X,Y)>0說明X與Y的變化趨勢是一致的,X增長的時候Y也隨著增長。如果X,Y互相獨立的話,cov(X,Y)=0. cov(X,X)=D(X),變數X與自身的協方差就是方差,cov(X,Y)=cov
Stanford機器學習-異常檢測和多元高斯分佈
一、異常檢測 這章主要學習異常檢測問題,它是機器演算法的一個常見應用,同時也對於我們生活中的很多問題有很大的幫助,總的來說,它主要用於非監督的學習問題。 那我們怎麼來理解異常檢測是一個怎麼樣的問題呢?我們來看一個相關的問題:飛機引擎的檢測。因為引擎對於飛機來說
Machine Learning第九講【異常檢測】-- (三)多元高斯分佈
一、Multivariate Gaussian Distribution(多元高斯分佈) 資料中心例子: 因為上面的原因,會帶來一些誤差,因此我們引入了改良版的演算法: 我們不再單獨地將p(x1),p(x2),p(x3)訓練模型,而是將這些引數都放在一個模型裡,
斯坦福大學機器學習筆記——異常檢測演算法(高斯分佈、多元高斯分佈、異常檢測演算法)
異常檢測問題介紹: 異常檢測演算法主要用於無監督學習問題,但從某種角度看它又類似於一種有監督學習的問題,下面我們從一個例子中簡單介紹一下什麼是異常檢測問題。 比如我們有一個飛機引擎製造商,對於一個新造出的飛機引擎我們想判斷這個引擎是不是異常的。 假如我們有
多元高斯分佈(斯坦福machine learning week 9)
1 背景 之前的異常檢測演算法,其實是以中心區域向外以正圓的形式擴散的。也就是說距離中心區域距離相等的點,對應的p(x)都是一樣的,所以我們可能無法檢測到這一個異常樣本,因為它也處在一個p(x)比較大的範圍內: 之前的也就是圓形的範圍,但是我們現在將要說
多元高斯分佈及多元條件高斯分佈
已知 D 維向量 x,其高斯概率分佈為: N(x|μ,Σ)==1(2π)D/21|Σ|1/2exp(−12(x−μ)TΣ−1(x−μ))1|Σ|(2π)D−−−−−−−√exp(−12(x−μ
多元高斯分佈的均值與協方差矩陣
多元高斯分佈,即資料的維度不再為1維度。 樣本個數記為n x特徵向量的維度為k 。 舉個例子: 樣本1:[2,3,4,5,6] 樣本2:[3,4,5,6,7] 樣本3:[4,5,6,7,8]; 求各個維度上的均值:x_i = [2+3+4/3,3+4+5/3.....6+7+8/3] == [3,4,5
機器學習-多元高斯分佈(異常檢測)
的系列文章進行學習。 不過博主的部落格只寫到“第十講 資料降維” http://blog.csdn.net/abcjennifer/article/details/8002329,後面還有三講,內容比較偏應用,分別是異常檢測、大資料機器學習、photo OCR。為了學習的完整性,我將把後續三講的內容補充
多變數高斯分佈之間的KL散度(KL Divergence)
單變數高斯分佈的概率密度函式如下(均值:u,方差:σ): N(x|u,σ)=1(2πσ2)1/2exp{−12σ2(x−u)2} 多變數高斯分佈(假設n維)的概率密度函式如下(均值:u,協方差矩陣:Σ): N(x|u,Σ)=1(2π)n/2|Σ|1/2ex
兩個多維高斯分佈之間的KL散度推導
在深度學習中,我們通常對模型進行抽樣並計算與真實樣本之間的損失,來估計模型分佈與真實分佈之間的差異。並且損失可以定義得很簡單,比如二範數即可。但是對於已知引數的兩個確定分佈之間的差異,我們就要通過推導的方式來計算了。 下面對已知均值與協方差矩陣的兩個多維高斯分佈之間的KL散度進行推導。當然,因為便於分
【機器學習】兩分佈間距離的度量:MMD、KL散度、Wasserstein 對比
MMD:最大均值差異 Wasserstein距離[1] 實驗 資料來源 Amazon review benchmark dataset. The Amazon review dataset is one of the most widely used b
資訊熵(夏農熵),相對熵(KL散度), 交叉熵 三者的對比以及 吉布斯不等式
各種各樣資訊科學中,無論是通訊還是大資料處理,各種“熵”是非常重要的,因為它可以度量隨機變數不確定度,量化資訊量的大小。 資訊熵(夏農熵) 首先複習一下資訊熵(夏農熵),輔助我們對相對熵和交叉熵的理解。 對於一個隨機變數XX,其可能的取值分別為X={x
異常檢測: 應用多元高斯分布進行異常檢測
ron 適用於 fff 可能性 方差 評估 估計 變量 strong 多元高斯(正態)分布 多元高斯分布有兩個參數u和Σ,u是一個n維向量,Σ協方差矩陣是一個n*n維矩陣。改變u與Σ的值可以得到不同的高斯分布。 參數估計(參數擬合),估計u和Σ的公式如上圖所示,u為平均值
信息熵,交叉熵,KL散度
老師 數據壓縮 定性 引入 理解 1.7 資料 衡量 我們 0 前言 上課的時候老師講到了信息論中的一些概念,看到交叉熵,這個概念經常用在機器學習中的損失函數中。 這部分知識算是機器學習的先備知識,所以查資料加深一下理解。 Reference: 信息熵是什麽,韓迪的回答:h
KL散度、交叉熵與極大似然 的友誼
ood 進行 映射 滿足 變量 rac 生成 ack kl散度 一. 信息論背景 信息論的研究內容,是對一個信號包含信息的多少進行量化。所采用的量化指標最好滿足兩個條件: (1)越不可能發生的事件包含的信息量越大; (2)獨立事件有增量的信息(就是幾個獨立事件同時發生的
顯著性檢測(saliency detection)評價指標之KL散度距離Matlab代碼實現
mean enc gray SM tla function cor 代碼 ati 步驟1:先定義KLdiv函數: function score = KLdiv(saliencyMap, fixationMap) % saliencyMap is the saliency
多元高斯分布(轉載)
平面 一個 而是 http 公式 info 參數 應該 不能 原博地址:https://www.cnblogs.com/yan2015/p/7406904.html 多元高斯分布(multivariate gaussian distribution)有一些優勢也有一些劣
KL散度的理解
gin tar 不同 技術 計算公式 概念 ive XML kl散度 原文地址Count Bayesie 這篇文章是博客Count Bayesie上的文章Kullback-Leibler Divergence Explained 的學習筆記,原文對 KL散度
[吳恩達機器學習筆記]15非監督學習異常檢測7-8使用多元高斯分布進行異常檢測
進行 平均值 info 錯誤 blog 占用 ron 關系 http 15.異常檢測 Anomaly detection 覺得有用的話,歡迎一起討論相互學習~Follow Me 15.7-8 多變量高斯分布/使用多元高斯分布進行異常檢測 -Multivariate Gaus

