多元高斯分佈

1.協方差矩陣

協方差衡量的是變數X與Y之間是否存線上性關係，cov(X,Y)>0說明X與Y的變化趨勢是一致的，X增長的時候Y也隨著增長。如果X，Y互相獨立的話，cov(X,Y)=0.

cov(X,X)=D(X)，變數X與自身的協方差就是方差，cov(X,Y)=cov(Y,X)，cov(X,Y)=E[(X-E(X))(Y-E(Y))].

注意，上述變數X,Y都是一維變數，因此他們的協方差是一個數，如果X∈，Y∈，那麼X,Y的協方差矩陣就是一個n*n的矩陣，也就是協方差矩陣，關於協方差矩陣的介紹可以檢視協方差矩陣.

一定要記住，期望，方差，協方差這些統計量都是針對的一維隨機變數來說的，傳統的高斯分佈也是針對一維隨機變數，通過平均數u和方差

協方差矩陣的定義上面已經說了，http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/介紹了一下Σ的意義，Σ實際上是一個線性變換函式，可以使用Σ來對原始資料D進行相應的變換，其中一些比較有用的話如下，具體請檢視部落格：

1.the largest eigenvector of the covariance matrix always points into the direction of the largest variance of the data, and the magnitude of this vector equals the corresponding eigenvalue

通過PCA我們知道，最大特徵值對應的特徵向量具有最大的方差，我感覺這裡說的比較好的一點就是方差越大資料的spread就越大，這一點可以通過下圖來看出：

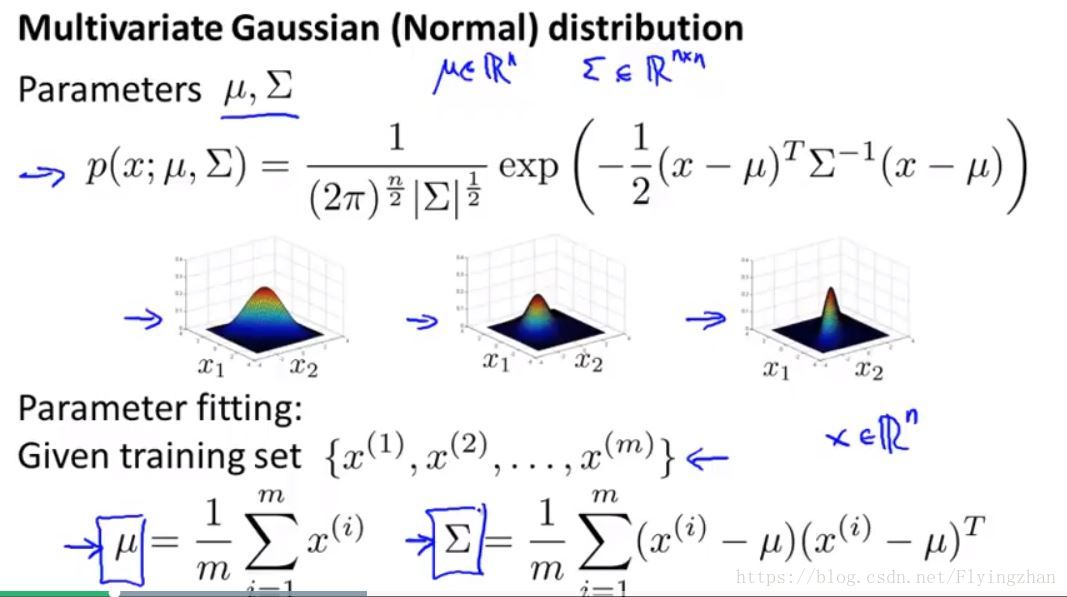
上圖擷取自andrew ng在coursera上的機器學習課程的multivariate gaussian distribution一節中，由於Σ對角線上的元素的值就是變數的方差，可以看出，當x2的方差等於1的時候大於0.6的時候。

2.we showed that the covariance matrix of observed data is directly related to a linear transformation of white, uncorrelated data. This linear transformation is completely defined by the eigenvectors and eigenvalues of the data. While the eigenvectors represent the rotation matrix, the eigenvalues correspond to the square of the scaling factor in each dimension.

2.多元高斯分佈

多元高斯分佈的詳細介紹請檢視部落格https://www.cnblogs.com/jermmyhsu/p/8251013.html，這裡我想說的主要是下面一點。如果我們需要估計一些資料分佈接近於高斯分佈的變數時，存在兩種解法。一種就是把特徵的第一維當做一個一維的變數，然後使用u1以及σ1來衡量他的分佈，同樣，對於第二維使用u2以及σ2來衡量，然後將得到的obj=p(x1; u1, σ1)*p(x2; u2, σ2)*...*p(xn; un, σn)來當做最終的目標函式進行優化，使用最大似然估計來得到較好的分佈估計。但是我們也可以使用多元高斯分佈來代替，此時p(x)=p(x;u,Σ).

通過求偏導我們可以得到u,Σ的最優解。

多元高斯分佈和上面所說的將第一維當做一個一維的變數，然後使用u1以及σ1來衡量他的分佈，同樣，對於第二維使用u2以及σ2來衡量，然後將得到的obj=p(x1; u1, σ1)*p(x2; u2, σ2)*...*p(xn; un, σn)的模型有著聯絡，後者是多元高斯分佈的一種特例，當n維變數X的每一維都相互獨立，也就是說多元高斯分佈對應的Σ是一個對角矩陣，除了主對角線上的數外，其餘數都為0，此時多元高斯分佈可以寫成上述形式，注意，模型obj沒有要求每一維是相互獨立的。

原始的模型計算複雜度比較小，多元高斯模型計算複雜度較大，但是效果更好。通過人為構造一些捕捉不同維度之間關係的維度能夠得到更好的效果，而當訓練樣本數遠大於資料維度的時候使用多元高斯分佈能夠取得很好的效果。