最近在做腦電訊號分析，在導師的建議下學習了一點經驗模式分解（下面簡稱EMD）的皮毛，期間也是遇到了很多問題，在這裡整理出來，一是為了自己備忘，二是為了能儘量幫到有需要的朋友。

一、EMD簡介

　　經驗模態分解（Empirical Mode Decomposition,EMD）法是黃鍔（N. E. Huang）在美國國家宇航局與其他人於1998年創造性地提出的一種新型自適應訊號時頻處理方法，特別適用於非線性非平穩訊號的分析處理。對經過EMD處理的訊號再進行希爾伯特變換，就組成了大名鼎鼎的“希爾伯特—黃變換”（HHT）。由於腦電訊號處理很少在EMD之後接上希爾伯特變換，在這裡僅介紹EMD的相關基礎知識。
　　EMD其實就是一種對訊號進行分解的方法，與傅立葉變換、小波變換的核心思想一致，大家都想將訊號分解為各個相互獨立的成分的疊加；只不過傅立葉變換以及小波變換都要求要有基函式，而EMD卻完全拋開了基函式的束縛，僅僅依據資料自身的時間尺度特徵來進行訊號分解，具備自適應性。由於無需基函式，EMD幾乎可以用於任何型別訊號的分解，尤其是在非線性、非平穩訊號的分解上具有明顯的優勢。
　　EMD的目的是將訊號分解為多個本徵模函式（IMF）的疊加。IMF必需要滿足以下兩個條件：
　　（1）函式在整個時間範圍內，區域性極值點和過零點的數目必須相等，或最多相差一個；
　　（2）在任意時刻點，區域性最大值的包絡（上包絡線）和區域性最小值的包絡（下包絡線） 平均必須為零。
　　為什麼IMF一定要滿足這兩個條件呢？經黃鍔等人的研究，滿足這兩個條件的訊號都是單組分的，相當於序列的每一個點只有一個瞬時頻率，無其他頻率組分疊加。這就為後續的希爾伯特變換鋪平了道路，也使得瞬時頻率有了意義。
　　值得一提的是，EMD在數學上還有一些細節無法證明，但是EMD已經在工程領域取得了輝煌的成就，這也是在科學界工程領先理論的一個例子。

二、EMD方法的實現

　　EMD的實現我決定簡單說一下，畢竟我們是使用者而已嘛^_^，有需要的朋友可以自行研究一下。
　　EMD方法是基於如下假設基礎上的：
　　（1）訊號至少有兩個極值點，一個極大值和一個極小值；
　　（2）特徵時間尺度通過兩個極值點之間的時間定義；
　　（3）若資料缺乏極值點但有形變點，則可通過資料微分一次或幾次獲得極值點，然後再通過積分來獲得分解結果。
　　演算法流程如下所示：
　　　　　　　　　　　　

三、Matlab工具箱安裝

　　在這裡我們需要下載兩個工具箱，第一個是時頻分析工具箱，下載地址為：http://tftb.nongnu.org/；另一個就是EMD工具箱，下載地址為：

http://perso.ens-lyon.fr/patrick.flandrin/emd.html。有些同學反映無法下載，現給出百度雲地址：https://pan.baidu.com/share/init?surl=-jOdWceZebqnK6kzO2Hhyg，密碼 stim。
　　第一步安裝時頻分析工具箱，安裝這個工具箱是因為EMD工具箱中的一些功能依賴於這個工具箱。安裝步驟如下：
　　（1）解壓下載的工具箱，將其複製到matlab的toolbox資料夾下
　　（2）建立搜尋路徑，matlab->設定路徑->新增幷包含子資料夾->找到在toolbox目錄下的時頻分析工具箱->儲存->關閉
　　第二步為安裝EMD工具箱，這個就簡單一些了，下載完畢直接執行“install_emd.m”就可以啦。如果在安裝之後，Matlab提示“cemdc2_fix.c等檔案安裝失敗”，如果想讓其編譯成功則可以參考這篇文章：

http://forum.vibunion.com/thread-79866-1-1.html，如果嫌麻煩的話，也可以不用修復，不會影響到使用EMD功能的。

四、程式演示

　　在這裡貼上一個小程式作為演示，也可以用來測試工具箱有沒有安裝好。　

fs = 1000;
ts = 1/fs;
t=0:ts:0.3;
z = sin(2*pi*10*t) + sin(2*pi*100*t);
imf=emd(z);
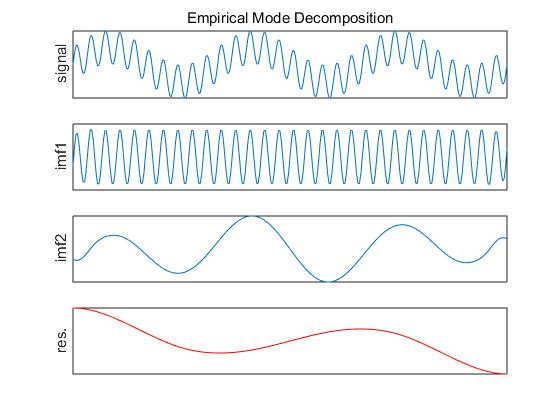
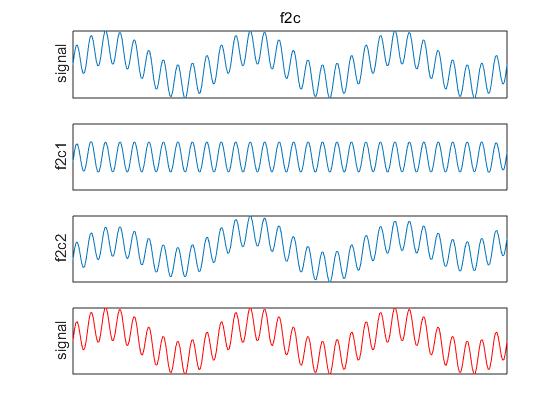
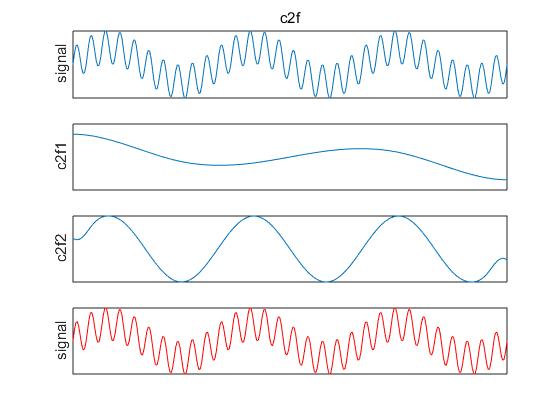
emd_visu(z,t,imf)  % EMD專用畫圖函式

執行完會出現3張圖，如下所示：