2. 程式人生 > >極限學習機（ELM） 演算法及MATLAB程式實現

極限學習機（ELM） 演算法及MATLAB程式實現

阿新 • • 發佈：2019-01-10

極限學習機

       單隱藏層反饋神經網路具有兩個比較突出的能力： 

（1）可以直接從訓練樣本中擬 合 出 復 雜 的 映 射 函 數f :x ^ t 

（2 ）可以為大量難以用傳統分類引數技術處理的自然或者人工現象提供模型。但是單隱藏層反饋神經網路缺少比較快速的學習方 法 。誤差反向傳播演算法每次迭代需要更新n x(L+ 1) +L x (m+ 1 )個 值 ，所花費的時間遠遠低於所容忍的時間。經常可以看到為訓練一個單隱藏層反饋神經網路花費了數小時，數天或者更多的時間。
       基於以上原因，黃廣斌教授對單隱藏層反饋神經網路進行了深入的研究，提
出並證明了兩個大膽的理論：


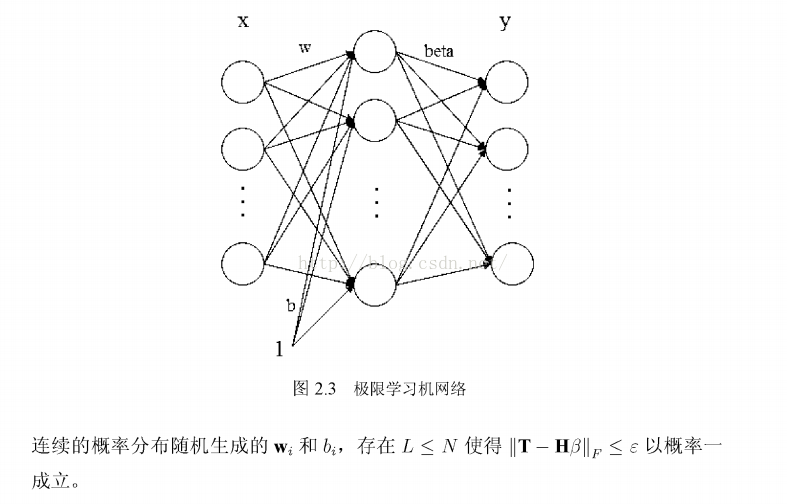
       從以上兩條理論我們可以看出，只要激勵函式

g:R ^ R滿足在任意區間上無限可微，那麼wt和bt可以從R的n維和R空間的任何區間內根據任意連續的概率分佈隨機生成 ，也就是說單隱藏層前饋神經網路無需再對wt和bt進行調整；又因為式子||TH*beta||_f=0以概率一成立，我們發現輸出層的偏置也不再需要。那麼一個新型的但隱藏層反饋神經網路如圖2 .3表示 。
對比圖2.2,缺少了輸出層偏 置bs,而輸入權重w和隱藏層偏置bi隨機產生不需要調整，那麼整個網路僅僅剩下輸出權重beta一項沒有確定。因此極限學習機
應運而生。令神經網路的輸出等於樣本標籤，如式 (2-11) 表示




n x(L+1) +Lx(m+1)個值,且反向傳播演算法為了保證系統的穩定性通常選取較小的學習率，使得學習時間大大加長。因此極限學習機在這一方法優勢非常巨大，在實驗中 ，極限學習機往往在數秒內就完成了運算。而一些比較經典的演算法在訓練一個單隱藏層神經網路的時候即使是很小的應用也要花費大量的時間，似乎這些演算法存在著一個無法逾越的虛擬速度壁壘。

(2)在大多數的應用中，極限學習機的泛化能力大於類似於誤差反向傳播演算法這類的基於梯度的演算法。
( 3 ) 傳統的基於梯度的演算法需要面對諸如區域性最小，合適的學習率、過擬合等問題 ，而極限學習機一步到位直接構建起單隱藏層反饋神經網路，避免了這些難以處理的棘手問題。
極限學習機由於這些優勢，廣大研究人員對極限學習機報以極大的興趣，使得這幾年極限學習機的理論發展很快，應用也在不斷地拓寬。
小結
本文主要對極限學習機的本質原理和來龍去脈作了詳盡的介紹，闡明極限學習機所具有的各種各樣優勢吸引廣大學者進行研究。然而極限學習機也有自己的劣勢，接下來我們將對極限學習機的劣勢進行分析和研究並加以改進。 

MATLAB程式：可以到GB.Huang老師

個人網站上下載

1、一個迴歸的例子：（資料、程式放在同一資料夾）

clear all;
close all;
clc;
[TrainingTime, TestingTime, TrainingAccuracy, TestingAccuracy] =   ELM('sinc_train', 'sinc_test', 0, 20, 'sig')

ELM.m

function [TrainingTime, TestingTime, TrainingAccuracy, TestingAccuracy] = elm(TrainingData_File, TestingData_File, Elm_Type, NumberofHiddenNeurons, ActivationFunction)

% Usage: elm(TrainingData_File, TestingData_File, Elm_Type, NumberofHiddenNeurons, ActivationFunction)
% OR:    [TrainingTime, TestingTime, TrainingAccuracy, TestingAccuracy] = elm(TrainingData_File, TestingData_File, Elm_Type, NumberofHiddenNeurons, ActivationFunction)
%
% Input:
% TrainingData_File     - Filename of training data set
% TestingData_File      - Filename of testing data set
% Elm_Type              - 0 for regression; 1 for (both binary and multi-classes) classification
% NumberofHiddenNeurons - Number of hidden neurons assigned to the ELM
% ActivationFunction    - Type of activation function:
%                           'sig' for Sigmoidal function
%                           'sin' for Sine function
%                           'hardlim' for Hardlim function
%                           'tribas' for Triangular basis function
%                           'radbas' for Radial basis function (for additive type of SLFNs instead of RBF type of SLFNs)
%
% Output: 
% TrainingTime          - Time (seconds) spent on training ELM
% TestingTime           - Time (seconds) spent on predicting ALL testing data
% TrainingAccuracy      - Training accuracy: 
%                           RMSE for regression or correct classification rate for classification
% TestingAccuracy       - Testing accuracy: 
%                           RMSE for regression or correct classification rate for classification
%
% MULTI-CLASSE CLASSIFICATION: NUMBER OF OUTPUT NEURONS WILL BE AUTOMATICALLY SET EQUAL TO NUMBER OF CLASSES
% FOR EXAMPLE, if there are 7 classes in all, there will have 7 output
% neurons; neuron 5 has the highest output means input belongs to 5-th class
%
% Sample1 regression: [TrainingTime, TestingTime, TrainingAccuracy, TestingAccuracy] = elm('sinc_train', 'sinc_test', 0, 20, 'sig')
% Sample2 classification: elm('diabetes_train', 'diabetes_test', 1, 20, 'sig')
%
    %%%%    Authors:    MR QIN-YU ZHU AND DR GUANG-BIN HUANG
    %%%%    NANYANG TECHNOLOGICAL UNIVERSITY, SINGAPORE
    %%%%    EMAIL:      [email protected]; [email protected]
    %%%%    WEBSITE:    http://www.ntu.edu.sg/eee/icis/cv/egbhuang.htm
    %%%%    DATE:       APRIL 2004

%%%%%%%%%%% Macro definition
REGRESSION=0;
CLASSIFIER=1;

%%%%%%%%%%% Load training dataset
train_data=load(TrainingData_File);
T=train_data(:,1)';
P=train_data(:,2:size(train_data,2))';
clear train_data;                                   %   Release raw training data array

%%%%%%%%%%% Load testing dataset
test_data=load(TestingData_File);
TV.T=test_data(:,1)';
TV.P=test_data(:,2:size(test_data,2))';
clear test_data;                                    %   Release raw testing data array

NumberofTrainingData=size(P,2);
NumberofTestingData=size(TV.P,2);
NumberofInputNeurons=size(P,1);

if Elm_Type~=REGRESSION
    %%%%%%%%%%%% Preprocessing the data of classification
    sorted_target=sort(cat(2,T,TV.T),2);
    label=zeros(1,1);                               %   Find and save in 'label' class label from training and testing data sets
    label(1,1)=sorted_target(1,1);
    j=1;
    for i = 2:(NumberofTrainingData+NumberofTestingData)
        if sorted_target(1,i) ~= label(1,j)
            j=j+1;
            label(1,j) = sorted_target(1,i);
        end
    end
    number_class=j;
    NumberofOutputNeurons=number_class;
       
    %%%%%%%%%% Processing the targets of training
    temp_T=zeros(NumberofOutputNeurons, NumberofTrainingData);
    for i = 1:NumberofTrainingData
        for j = 1:number_class
            if label(1,j) == T(1,i)
                break; 
            end
        end
        temp_T(j,i)=1;
    end
    T=temp_T*2-1;

    %%%%%%%%%% Processing the targets of testing
    temp_TV_T=zeros(NumberofOutputNeurons, NumberofTestingData);
    for i = 1:NumberofTestingData
        for j = 1:number_class
            if label(1,j) == TV.T(1,i)
                break; 
            end
        end
        temp_TV_T(j,i)=1;
    end
    TV.T=temp_TV_T*2-1;

end                                                 %   end if of Elm_Type

%%%%%%%%%%% Calculate weights & biases
start_time_train=cputime;

%%%%%%%%%%% Random generate input weights InputWeight (w_i) and biases BiasofHiddenNeurons (b_i) of hidden neurons
InputWeight=rand(NumberofHiddenNeurons,NumberofInputNeurons)*2-1;
BiasofHiddenNeurons=rand(NumberofHiddenNeurons,1);
tempH=InputWeight*P;
clear P;                                            %   Release input of training data 
ind=ones(1,NumberofTrainingData);
BiasMatrix=BiasofHiddenNeurons(:,ind);              %   Extend the bias matrix BiasofHiddenNeurons to match the demention of H
tempH=tempH+BiasMatrix;

%%%%%%%%%%% Calculate hidden neuron output matrix H
switch lower(ActivationFunction)
    case {'sig','sigmoid'}
        %%%%%%%% Sigmoid 
        H = 1 ./ (1 + exp(-tempH));
    case {'sin','sine'}
        %%%%%%%% Sine
        H = sin(tempH);    
    case {'hardlim'}
        %%%%%%%% Hard Limit
        H = double(hardlim(tempH));
    case {'tribas'}
        %%%%%%%% Triangular basis function
        H = tribas(tempH);
    case {'radbas'}
        %%%%%%%% Radial basis function
        H = radbas(tempH);
        %%%%%%%% More activation functions can be added here                
end
clear tempH;                                        %   Release the temparary array for calculation of hidden neuron output matrix H

%%%%%%%%%%% Calculate output weights OutputWeight (beta_i)
OutputWeight=pinv(H') * T';                        % implementation without regularization factor //refer to 2006 Neurocomputing paper
%OutputWeight=inv(eye(size(H,1))/C+H * H') * H * T';   % faster method 1 //refer to 2012 IEEE TSMC-B paper
%implementation; one can set regularizaiton factor C properly in classification applications 
%OutputWeight=(eye(size(H,1))/C+H * H') \ H * T';      % faster method 2 //refer to 2012 IEEE TSMC-B paper
%implementation; one can set regularizaiton factor C properly in classification applications

%If you use faster methods or kernel method, PLEASE CITE in your paper properly: 

%Guang-Bin Huang, Hongming Zhou, Xiaojian Ding, and Rui Zhang, "Extreme Learning Machine for Regression and Multi-Class Classification," submitted to IEEE Transactions on Pattern Analysis and Machine Intelligence, October 2010. 

end_time_train=cputime;
TrainingTime=end_time_train-start_time_train        %   Calculate CPU time (seconds) spent for training ELM

%%%%%%%%%%% Calculate the training accuracy
Y=(H' * OutputWeight)';                             %   Y: the actual output of the training data
if Elm_Type == REGRESSION
    TrainingAccuracy=sqrt(mse(T - Y))               %   Calculate training accuracy (RMSE) for regression case
end
clear H;

%%%%%%%%%%% Calculate the output of testing input
start_time_test=cputime;
tempH_test=InputWeight*TV.P;
clear TV.P;             %   Release input of testing data             
ind=ones(1,NumberofTestingData);
BiasMatrix=BiasofHiddenNeurons(:,ind);              %   Extend the bias matrix BiasofHiddenNeurons to match the demention of H
tempH_test=tempH_test + BiasMatrix;
switch lower(ActivationFunction)
    case {'sig','sigmoid'}
        %%%%%%%% Sigmoid 
        H_test = 1 ./ (1 + exp(-tempH_test));
    case {'sin','sine'}
        %%%%%%%% Sine
        H_test = sin(tempH_test);        
    case {'hardlim'}
        %%%%%%%% Hard Limit
        H_test = hardlim(tempH_test);        
    case {'tribas'}
        %%%%%%%% Triangular basis function
        H_test = tribas(tempH_test);        
    case {'radbas'}
        %%%%%%%% Radial basis function
        H_test = radbas(tempH_test);        
        %%%%%%%% More activation functions can be added here        
end
TY=(H_test' * OutputWeight)';                       %   TY: the actual output of the testing data
end_time_test=cputime;
TestingTime=end_time_test-start_time_test           %   Calculate CPU time (seconds) spent by ELM predicting the whole testing data

if Elm_Type == REGRESSION
    TestingAccuracy=sqrt(mse(TV.T - TY));            %   Calculate testing accuracy (RMSE) for regression case
end
if Elm_Type == REGRESSION
    figure
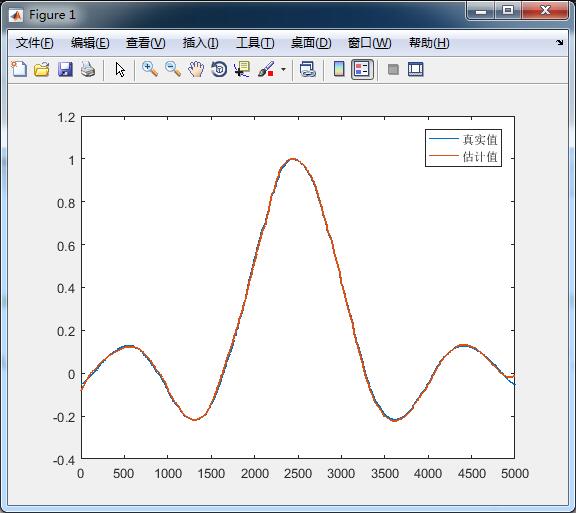
    plot(TV.T,'LineWidth',1.2);hold on ;
    plot(TY,'LineWidth',1.2)
    legend('真實值','估計值')
end
if Elm_Type == CLASSIFIER
%%%%%%%%%% Calculate training & testing classification accuracy
    MissClassificationRate_Training=0;
    MissClassificationRate_Testing=0;

    for i = 1 : size(T, 2)
        [x, label_index_expected]=max(T(:,i));
        [x, label_index_actual]=max(Y(:,i));
        if label_index_actual~=label_index_expected
            MissClassificationRate_Training=MissClassificationRate_Training+1;
        end
    end
    TrainingAccuracy=1-MissClassificationRate_Training/size(T,2)
    for i = 1 : size(TV.T, 2)
        [x, label_index_expected]=max(TV.T(:,i));
        [x, label_index_actual]=max(TY(:,i));
        if label_index_actual~=label_index_expected
            MissClassificationRate_Testing=MissClassificationRate_Testing+1;
        end
    end
    TestingAccuracy=1-MissClassificationRate_Testing/size(TV.T,2)  
end

測試結果：



TrainingTime =0.1248

TestingTime = 0

TrainingAccuracy = 0.1158

TestingAccuracy =0.0074


2、一個分類的例子

clear all;
close all;
clc;
[TrainingTime, TestingTime, TrainingAccuracy, TestingAccuracy] =  ELM('diabetes_train', 'diabetes_test', 1, 20, 'sig')

ELM.m還是上面的那個

模擬結果：

TrainingTime =0.0624

TestingTime = 0

TrainingAccuracy = 0.7674

TestingAccuracy =0.7865

歡迎評論，點贊！

相關推薦

極限學習機（ELM） 演算法及MATLAB程式實現

極限學習機       單隱藏層反饋神經網路具有兩個比較突出的能力： （1）可以直接從訓練樣本中擬 合 出 復 雜 的 映 射 函 數f :x ^ t （2 ）可以為大量難以用傳統分類引數技術處理的自然或者人工現象提供模型。但是單隱藏層反饋神經網路缺少比較快速的學習方 法 。

論戰Yann LeCun：誰能解釋極限學習機（ELM）牛X在哪裡？

摘要：ELM演算法執行過程中不必調整網路的輸入權值以及隱元的偏置，學習速度快且泛化效能好，Yann LeCun質疑ELM存在命名、方法論方面存在問題，ELM發明者則認為，ELM和深度學習是相輔相成的，並且ELM可以填補CNN的理論空白。 【編者按】被認為學習速度快、泛化效能

支援向量機（SVM）演算法的matlab的實現

支援向量機（SVM）的matlab的實現 支援向量機是一種分類演算法之一，matlab中也有相應的函式來對其進行求解；下面貼一個小例子，這個例子來源於我們實際的專案。 clc; clear; N=10; %下面的資料是我們實際專案中的訓練樣例（樣例中有8個屬

機器學習-支援向量機（SVM）演算法學習筆記

假設有訓練集D={(x1, y1), (x2, y2), ..., (xm, ym)}，yi{-1, 1}，分類學習最基本的想法就是基於訓練集D在樣本空間中找到一個劃分超平面，將不同類別的樣本分開。

多層感知機（MLP）演算法原理及Spark MLlib呼叫例項（Scala/Java/Python）

多層感知機 演算法簡介：         多層感知機是基於反向人工神經網路（feedforwardartificial neural network）。多層感知機含有多層節點，每層節點與網路的下一層節點完全連線。輸入層的節點代表輸入資料，其他層的節點通過將輸入資料與層上節點

MLlib--多層感知機（MLP）演算法原理及Spark MLlib呼叫例項（Scala/Java/Python）

來源：http://blog.csdn.net/liulingyuan6/article/details/53432429 多層感知機 演算法簡介：         多層感知機是基於反向人工神經網路（feedforwardartificial neural net

【轉】Nodejs學習筆記（一）--- 簡介及安裝Node.js開發環境

ack 目錄 javascrip 難度 時間 網站開發 clas jetbrains 常用 目錄 學習資料 簡介 安裝Node.js npm簡介 開發工具 Sublime Node.js開發環境配置 擴展：安裝多版本管理器 學習資料 　　1.深入淺出Node.j

Redis深入學習筆記（三）RDB及AOF流程

del 每秒調用 查看 單個 一個 重寫 use 物理內存 深入學習 RDB是Redis持久化數據的一種方式，是執行時間點的Redis內存快照，redis數據還原時加載rdb文件，Redis的主從數據同步也是基於RDB實現的。 RDB流程：

Golang學習筆記（五）常量及iota

Golang語言申明常量，需要用到一個關鍵字const。 const STR1 string = "hello" 大家習慣性的將常量設定為全大寫，但在Golang裡面是沒有private、public等許可權設定的，這些許可權僅靠方法、函式、變數等的首字母大小寫來設定，所以如果全大寫，將

4.支援向量機（SVM）演算法(下）

1.SVM演算法的特點  1.1 訓練好的模型的演算法複雜度是由支援向量的個數決定的，而不是由資料的維度決定的。 所有SVM不太容易產生overfitting 1.2 SVM訓練出來的模型完全依賴於支援向量（Support Vectors），即使訓練集裡面所有非支援向量的點都

3.支援向量機（SVM）演算法(上）

SVM 1.基本概念 支援向量機（Support Vector Machine, SVM）的基本模型是在特徵空間上找到最佳的分離超平面使得訓練集上正負樣本間隔最大。SVM是用來解決二分類問題的有監督學習演算法，在引入了核方法之後SVM也可以用來解決非線性問題。  一般SVM有下面三

HIVE簡明教程學習筆記（一）——資料庫及表的操作HIVE DDL

1.建立資料庫 create database if not exists aa_db; 2.檢視資料庫定義 describe database aa_db; 3.檢視資料庫列表 show databases; 4.刪除資料庫 drop database if exists testdb casca

嵌入式核心及驅動開發之學習筆記（七） 非阻塞模式+中斷實現讀取資料

當中斷髮生時，驅動程式會跳轉到中斷處理的函式入口，實現了中斷的捕獲和處理，但這樣還不夠。要讓使用者能夠獲取到中斷分析的結果，我們將建立一個描述中斷事件的結構體物件。硬體產生中斷後，驅動程式碼將對中斷事件的分析結果儲存在結構體變數中，使用者需要的時候，直接通過介面函式獲取這個結構體的資料。 核心層

圖解演算法學習筆記（一）: 演算法簡介

本章內容：     編寫第一種查詢演算法——二分查詢。     學習如何談論演算法的執行時間——大O表示法。 1) 演算法是一組完成任務的指令，任何程式碼片段都可視為演算法。 2)二分查詢：一種查詢演算法，其輸入是一個有序的元素列表。 Python實現二分查詢程式碼：

二叉樹後序遍歷（遞迴與非遞迴）演算法及C語言實現

二叉樹後序遍歷的實現思想是：從根節點出發，依次遍歷各節點的左右子樹，直到當前節點左右子樹遍歷完成後，才訪問該節點元素。 圖 1 二叉樹   如圖 1 中，對此二叉樹進行後序遍歷的操作過程為： 從根節點 1 開始，遍歷該節點的左子樹（以節點 2 為根節點）； 遍歷節點 2 的左子樹（以節點 4 為根

二叉樹中序遍歷（遞迴和非遞迴）演算法及C語言實現

二叉樹中序遍歷的實現思想是： 訪問當前節點的左子樹； 訪問根節點； 訪問當前節點的右子樹； 圖 1 二叉樹   以圖  1 為例，採用中序遍歷的思想遍歷該二叉樹的過程為： 訪問該二叉樹的根節點，找到 1； 遍歷節點 1 的左子樹，找到節點 2； 遍歷節點 2 的左子樹，找到節點 4；

深度學習基礎（一） —— softmax 及 logsoftmax

                softmax：重新定義了多層神經網路的輸出層（output layer），注意僅和輸出層有關係，和其他層無關。softmax function，也稱為 normalized exponential（指數族分佈的觀點）；1. softmax我們知道在神經網路的前饋（feedfo

QT學習筆記（一）——初識及訊號槽使用

１、hello world #include "gofuther.h" #include <QApplication> #include <QPushButton>//button #include <QLabel> int main(int argc,

Thymeleaf學習記錄（5）--運算及表單

Thymeleaf文字及預算： 字面 文字文字：'one text'，'Another one!'，... 號碼文字：0，34，3.0，12.3，... 布林文字：true，false 空字面： null 文字標記：one，sometext，m

Linux 學習筆記（一）使用者及使用者組

Linux 是個多使用者的作業系統，同一時間可以多個使用者，同時登入，同時操作檔案。由於安全需要，使用者管理應用而生。 但不同的使用者可能不同的許可權限制，如果每個使用者都要去處理這個使用者什麼檔案能訪問什麼檔案不能訪問，那也太煩了。使用者組的設定就很大程度減輕管理的壓力，使用者要有什麼許可權把使用者加到使