poj Intersection 1410 (數學幾何 求線段方程)
阿新 • • 發佈:2019-01-31
Intersection
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)
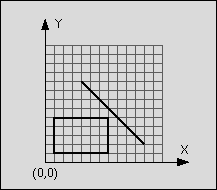
Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
| Time Limit: 1000MS | Memory Limit: 10000K |
| Total Submissions: 13147 | Accepted: 3426 |
Description
You are to write a program that has to decide whether a given line segment intersects a given rectangle.An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)

Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
Input
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
Output
Sample Input
1 4 9 11 2 1 5 7 1
Sample Output
F
題意
給定一條線段的起點和終點,再給定一個矩形的起點和終點(對角線兩點),問線段是否和矩形所包含的區域有交點。
思路:
先求出線段所在直線的方程a*x+b*y+c=0;(用到最原始的求直線方程的公式(可能是小學或者初中學的,但當時就是不知道咋寫.......))。
然後判斷線段是否與矩形所在區域有交點。具體看程式碼。。。
#include<stdio.h>
#include<string.h>
struct zz
{
int x;
int y;
}lb,le,sb,se;
int main()
{
int t,num1,num2;
int a,b,c,s;
scanf("%d",&t);
while(t--)
{
scanf("%d%d%d%d%d%d%d%d",&lb.x,&lb.y,&le.x,&le.y,&sb.x,&sb.y,&se.x,&se.y);
{
a=lb.y-le.y;
b=le.x-lb.x;
c=le.y*lb.x-lb.y*le.x;
if(sb.x>se.x)
{
s=sb.x;sb.x=se.x;se.x=s;
}
if(sb.y<se.y)
{
s=sb.y;sb.y=se.y;se.y=s;
}
num1=(a*sb.x+b*sb.y+c)*(a*se.x+b*se.y+c);
num2=(a*sb.x+b*se.y+c)*(a*se.x+b*sb.y+c);
if(num1>0&&num2>0)
{
printf("F\n");
continue;
}
if((lb.x<sb.x&&le.x<sb.x)||(lb.x>se.x&&le.x>se.x)||(lb.y>sb.y&&le.y>sb.y)||(lb.y<se.y&&le.y<se.y))
printf("F\n");
else
printf("T\n");
}
}
return 0;
}