GCO3.0的圖割分割演算法應用(三)
一)準備之前
對於一副影象分割之前,需要確定分割成幾類,這裡以灰度影象為例(彩色影象略複雜),通常來說分割成幾類只有兩種情況:事先知道該分成幾類或者實現不知道該分成幾類(這就是自適應分割了)。該工具箱應該是對於事先知不知道幾類的都可以處理,對於自適應分割只要找到對應的分割準則即可。為了簡單起見,這裡以知道類別數來進行實驗。
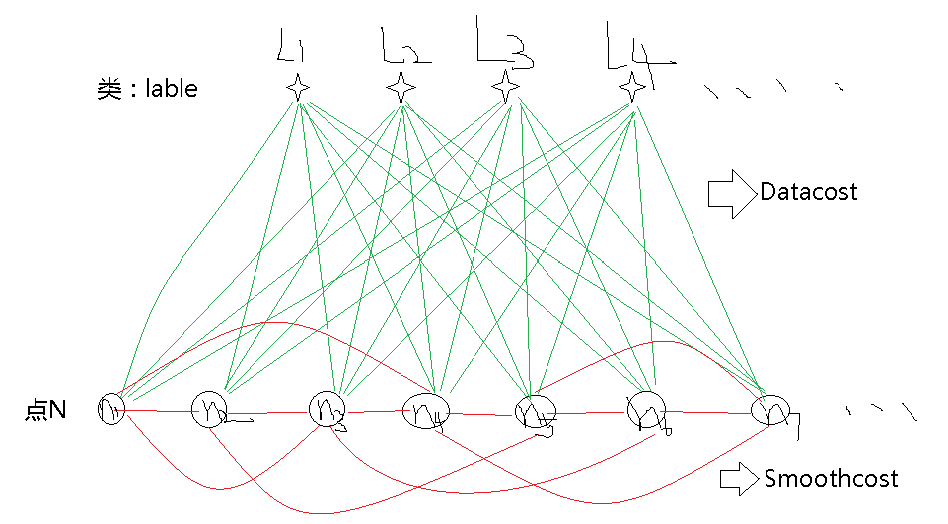
選擇經典的lena影象,並將其分割成5類。回顧下圖割理論,關於圖割中圖的構造主要包括兩個部分的邊權值:點與類中心之間的權值、點與點之間的權值。對於這兩部分都以簡單的影象灰度資訊來構造,點與類中心之間的權值按照點的灰度值與類中心的灰度值差值的平方來計算。點與點之間的權值也可以直接按照灰度相差來計算的,這裡以文獻上常用的方法來計算。
二)點與類中心權值-datacost
要計算點與類中心的權值大小,點的灰度知道(原始影象就是),那麼需要知道類中心的權值,因此需要對影象進行初始化預分類得到開始的一個分類標籤,從而得到初始的類中心。這以kmeans來進行預分類如下:
%k-means預分類找到中心與分類
%init_lable預分類,列向量; ctrs-類中心灰度值值
[init_lable,ctrs] = kmeans(img(:),Numlables); %img(:)通過索引轉化為列向量可用其中Numlables是定義的分類數(5),matlab自帶的kmeans方法理論上適用於一維情況,而影象是二維的,因此需要把影象轉化以一條長鏈(一維)才能用,得到的ctrs就是開始的類中心(灰度)。然後需要計算的就是所有點中,每個點相對於每個類中心的邊權值。把上節畫的圖再用一遍,形象的相關權值定義如下:
可以看到的datacost,這裡每個datacost計算方式為
function datacost = Datacost1(img,ctrs)
[m,n] = size(img);
num_lables = size(ctrs,1);
totalsizes = m*n;
datacost = zeros(totalsizes,num_lables);
for i = 1:totalsizes
Ip = double(img(i));
for j = 1:num_lables
datacost(i,j) = (Ip - ctrs(j 三)點與點之間的權值-neighbours
這一項描述的是一個領域項,認為每個點與周圍的四領域或者8領域內的畫素點有聯絡(也就是邊權值有值),與其他剩下的所有點沒有關係(邊權值為0),相鄰的畫素點之間的邊權值大小的計算方式為:
式中,sigma為整幅影象的方差。看過前面的知道,這個矩陣是相當的大((m*n)*(m*n))(m,n影象大小),且是個稀疏矩陣,要是每個元素都儲存起來根本儲存不下來,這裡以稀疏矩陣的方法儲存。
生成該權值矩陣的函式如下:
%%-------------------
% 每個點的灰度作為特徵
%%-------------------
function Neighbours = neighbours1(img)
[m,n] = size(img);
totalsizes = m*n;
var_img = var(img(:)); %影象方差
%% 選擇neigh=4四連通計算權值,neigh=8八連通計算權值
neigh = 4;
%%
if neigh == 4
%構建索引向量--生成距離的稀疏矩陣
i1 = (1:totalsizes-m)';
j1 = i1+m;
for i = 1:n
i2_tem(:,i) = (i-1)*m + (1:m-1)';
end
i2 = i2_tem(:);
j2 = i2+1;
%對應邊的值
ans1 = exp(-(img(i1(:))-img(j1(:))).^2/(2*var_img));
ans2 = exp(-(img(i2(:))-img(j2(:))).^2/(2*var_img));
%組合相應的向量:x位置,y位置,權值(注意必須都是列向量)
all = [[i1;i2],[j1;j2],[ans1;ans2]];
else
%構建索引向量--生成距離的稀疏矩陣
i1 = (1:totalsizes-m)'; %正右權值
j1 = i1+m;
for i = 1:n %正下權值
i2_tem(:,i) = (i-1)*m + (1:m-1)';
end
i2 = i2_tem(:);
j2 = i2+1;
for i = 1:n-1 %斜下權值
i3_tem(:,i) = (i-1)*m + (1:m-1)';
end
i3 = i3_tem(:);
j3 = i3+n+1;
i4 = i3+1; %斜上權值
j4 = i3+m;
%對應邊的值
ans1 = exp(-(img(i1(:))-img(j1(:))).^2/(2*var_img));
ans2 = exp(-(img(i2(:))-img(j2(:))).^2/(2*var_img));
ans3 = exp(-(img(i3(:))-img(j3(:))).^2/(2*var_img));
ans4 = exp(-(img(i4(:))-img(j4(:))).^2/(2*var_img));
%組合相應的向量:x位置,y位置,權值(注意必須都是列向量)
all = [[i1;i2;i3;i4],[j1;j2;j3;j4],[ans1;ans2;ans3;ans4]];
end
%matlab函式生成稀疏矩陣(這麼做的速度最快) %----------------
neighb = spconvert(all);
neighb(totalsizes,totalsizes) = 0;
Neighbours = neighb;再有就是上一個部落格說到,這個工具箱的實際點與點之間的權值大小並不是單純的Neighbours,而是在Neighbours 基礎上乘以一個SmoothCost,這裡為了直接使用到Neighbours,將SmoothCost設定為1即可。而這就是potts模型。相關設定:
%設定smoothcost
%不設定的時候預設使用potts模型
SmoothCost = eye(Numlables);
SmoothCost = 1 - SmoothCost;
GCO_SetSmoothCost(h,SmoothCost);四)可以開始了
在設定好了相關權值引數後,剩下的就是把這些組合起來了。前面說過,圖割是以能量函式的方式最小化方式進行的,當所有部分的能量達到最小的時候輸出最優結果(圖割得到的結果當然也只是一個區域性最優解,因為這個分割問題也是一個NP難問題,因此每一次執行的最終能量值不一樣,但是也不能差太多)。像上述的我們只涉及到了兩類能量,一個是點與類之間不同的一個能量,一個是點與點(領域項)之間不同的一個能量,而這兩個能量我們再用一個potts模型引數來控制他們之間的比例關係,這個比例關係也決定了最後分割的樣子。試著從理論上去分析一下,點與點(領域項)之間的這個能量其實是控制區域性平滑的一個約束項,如果這一項能量佔比重越大,認為分割影象之間就應該越平滑,那麼帶來的分割效果就是影象分割的越光滑,而這又帶來的另一個問題就是影象的細節保留的就少了,怎麼權衡這個引數就是需要進一步研究的地方。下面給出綜合起來的主程式:
clc;
clear;
%讀取影象
img = imread('lena.jpg');
img = double(rgb2gray(img));
%定義分類數 Numlables
Numlables = 5;
%定義Potts模型引數K
Potts_K = 100;
[m,n] = size(img);
totalsizes = m*n;
%k-means預分類找到中心與分類
%init_lable預分類,列向量; ctrs-類中心灰度值值
[init_lable,ctrs] = kmeans(img(:),Numlables); %img通過索引轉化為列向量可用
ctrs_new = zeros(Numlables,1);
%生成目標體
h = GCO_Create(totalsizes,Numlables);
%設定初始標籤
%% 已知初始化
GCO_SetLabeling(h,init_lable);
%設定datacost項
datacost = Datacost1(img,ctrs);
datacost = datacost';
GCO_SetDataCost(h,datacost);
%設定smoothcost
%不設定的時候預設使用potts模型
SmoothCost = eye(Numlables);
SmoothCost = 1 - SmoothCost;
GCO_SetSmoothCost(h,SmoothCost);
%設定neighbors項
Neighbours = Potts_K*neighbours1(img);
GCO_SetNeighbors(h,Neighbours);
%顯示輸出結果
GCO_SetVerbosity(h,2);
%類標籤運算順序
GCO_SetLabelOrder(h,randperm(Numlables));
%膨脹演算法
GCO_Expansion(h);
%獲得該標籤lables
Labeling = GCO_GetLabeling(h); %列向量
% 釋放記憶體
GCO_Delete(h);
%顯示graph cut分類
for i = 1:length(Labeling)
img1(i) = ctrs(Labeling(i));
end
img1 = reshape(img1,m,n);
%%
%繪製分割圖
figure;
%原影象
subplot(1,2,1);imshow(img,[]);
title('原始影象');
%顯示graph cut分類
subplot(1,2,2);imshow(img1,[]);
title(['Potts模型引數:',num2str(Potts_K)]); 五)實驗結果
potts模型引數的不同帶來影象的分割效果不同,下面給出potts模型引數從100-2000之間的過程中的執行結果:






這是一次執行過程中的能量值變化:
gco>> starting alpha-expansion w/ adaptive cycles
gco>> initial energy: E=8459828 (E=6728394+1731434+0)
gco>> after expansion(4): E=8378569 (E=6778690+1599879+0); 50177 vars; (1 of 5); 23.75 ms
gco>> after expansion(5): E=8357847 (E=6793528+1564319+0); 52615 vars; (2 of 5); 23.76 ms
gco>> after expansion(2): E=8340678 (E=6806374+1534304+0); 56583 vars; (3 of 5); 28.67 ms
gco>> after expansion(3): E=8307729 (E=6832920+1474809+0); 52857 vars; (4 of 5); 30.01 ms
gco>> after expansion(1): E=8264986 (E=6866636+1398350+0); 48939 vars; (5 of 5); 23.84 ms
gco>> after cycle 1: E=8264986 (E=6866636+1398350+0); 5 expansions(s);
gco>> after expansion(4): E=8264958 (E=6866999+1397959+0); 49960 vars; (1 of 5); 23.78 ms
gco>> after expansion(5): E=8264958 (E=6866999+1397959+0); 52571 vars; (2 of 5); 23.74 ms
gco>> after expansion(1): E=8264958 (E=6866999+1397959+0); 48394 vars; (3 of 5); 22.35 ms
gco>> after expansion(3): E=8264958 (E=6866999+1397959+0); 52498 vars; (4 of 5); 28.39 ms
gco>> after expansion(2): E=8264958 (E=6866999+1397959+0); 56684 vars; (5 of 5); 28.51 ms
gco>> after cycle 2: E=8264958 (E=6866999+1397959+0); 5 expansions(s);
gco>> after expansion(4): E=8264958 (E=6866999+1397959+0); 49953 vars; (1 of 1); 26.76 ms
gco>> after cycle 3: E=8264958 (E=6866999+1397959+0); 1 expansions(s);
gco>> after expansion(2): E=8264958 (E=6866999+1397959+0); 56684 vars; (1 of 4); 26.40 ms
gco>> after expansion(5): E=8264958 (E=6866999+1397959+0); 52571 vars; (2 of 4); 24.81 ms
gco>> after expansion(1): E=8264958 (E=6866999+1397959+0); 48394 vars; (3 of 4); 27.76 ms
gco>> after expansion(3): E=8264958 (E=6866999+1397959+0); 52498 vars; (4 of 4); 24.38 ms
gco>> after cycle 4: E=8264958 (E=6866999+1397959+0); 4 expansions(s);
六)到總結了
從上面的結果可以看出,potts模型引數越大,帶來的影象分割越平滑,對細節的保留就越少,而對於基礎圖割演算法的改進方法一般就是對這兩個能量函式進行改進,改進能量函式的邊權值計算方法,能量函式的構造方法,能量函式的尋優方式等等,當然很多問題還得就實際問題實際分析,分割方法沒有最好,只有更適合,其實也有最好,那就是人眼分割–計算機視覺與人工智慧的終極目標……