一、偏倚（bias）和方差(variance)

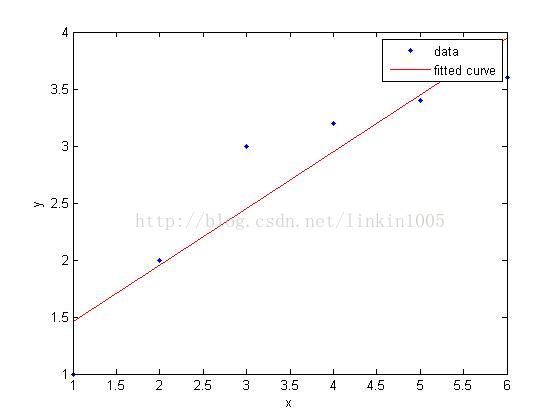
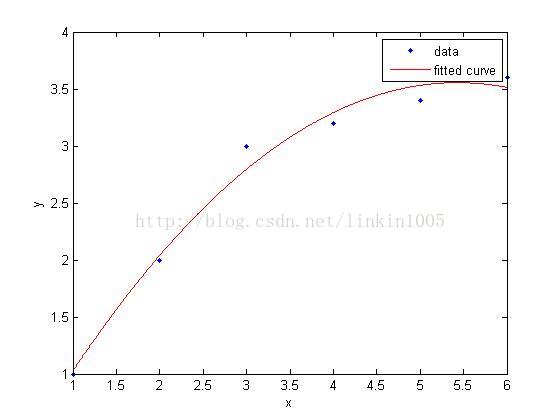
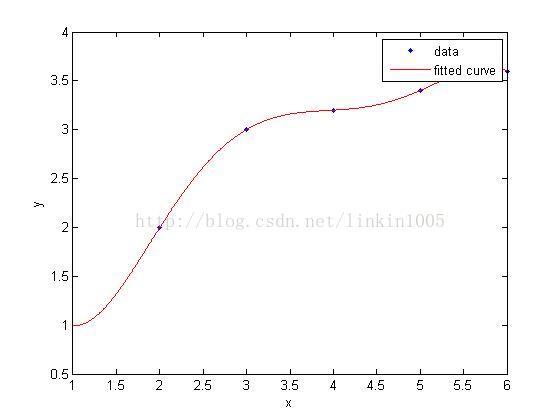
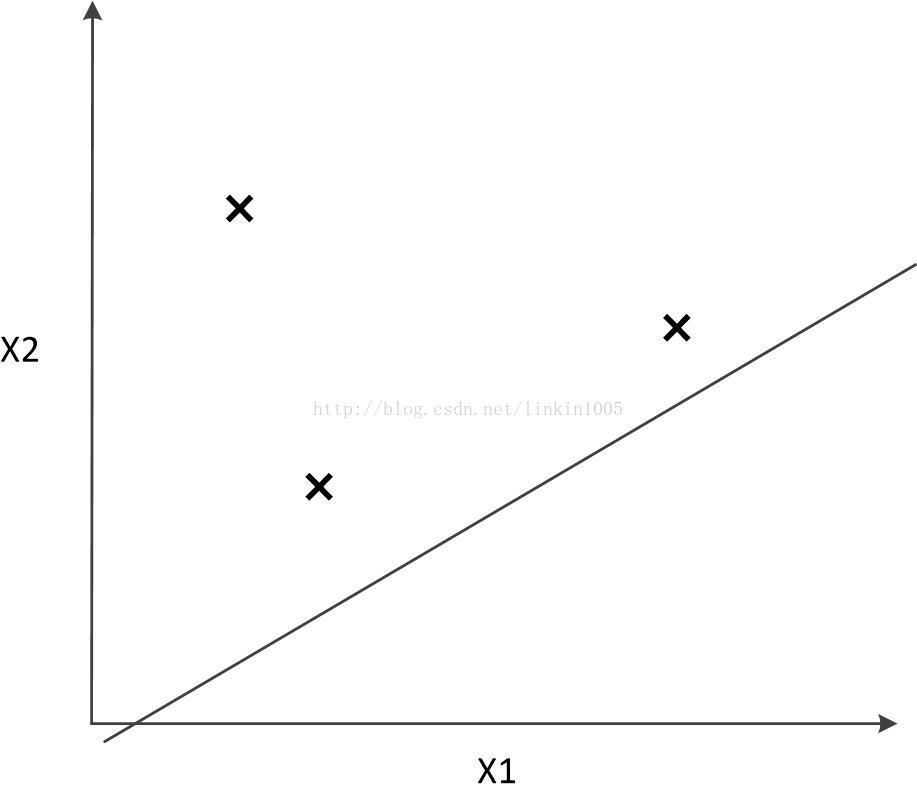
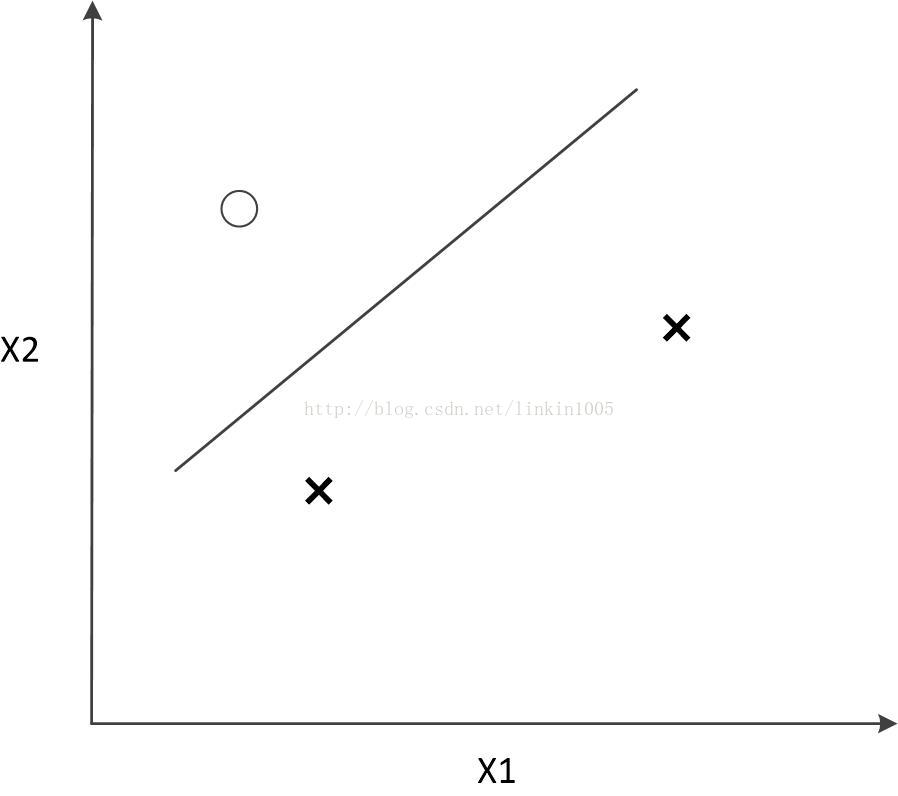
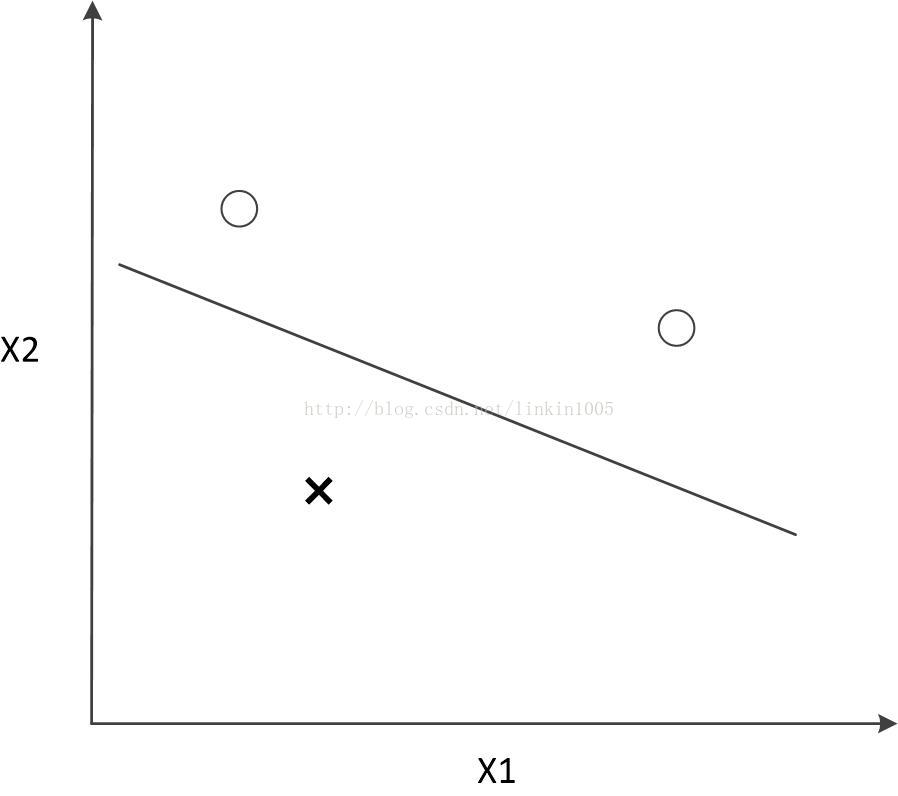
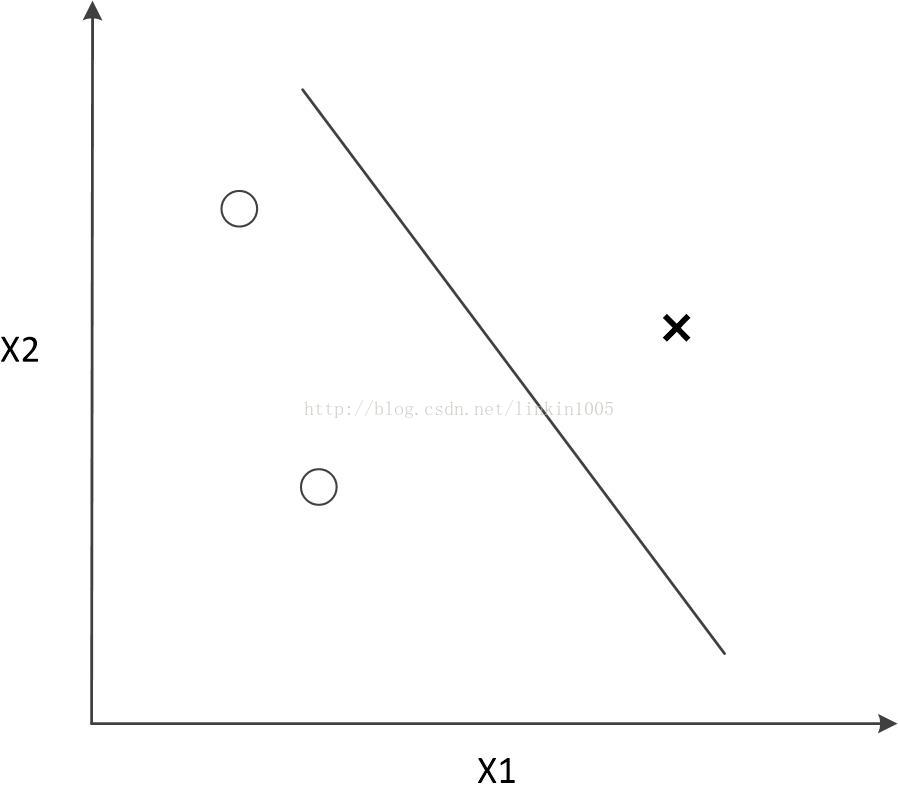
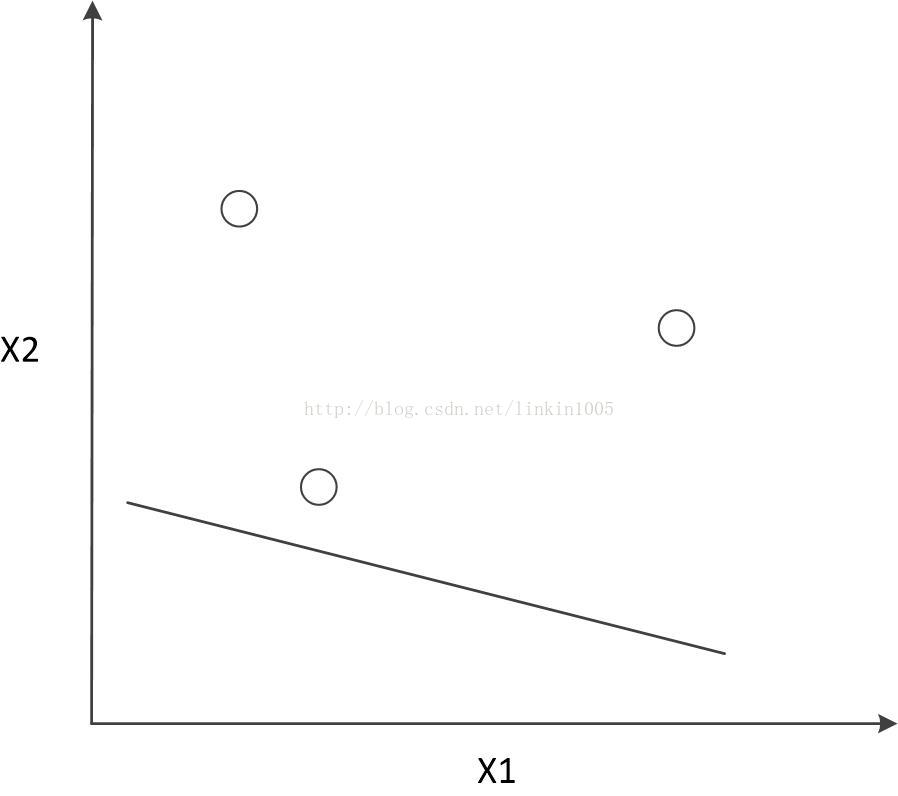
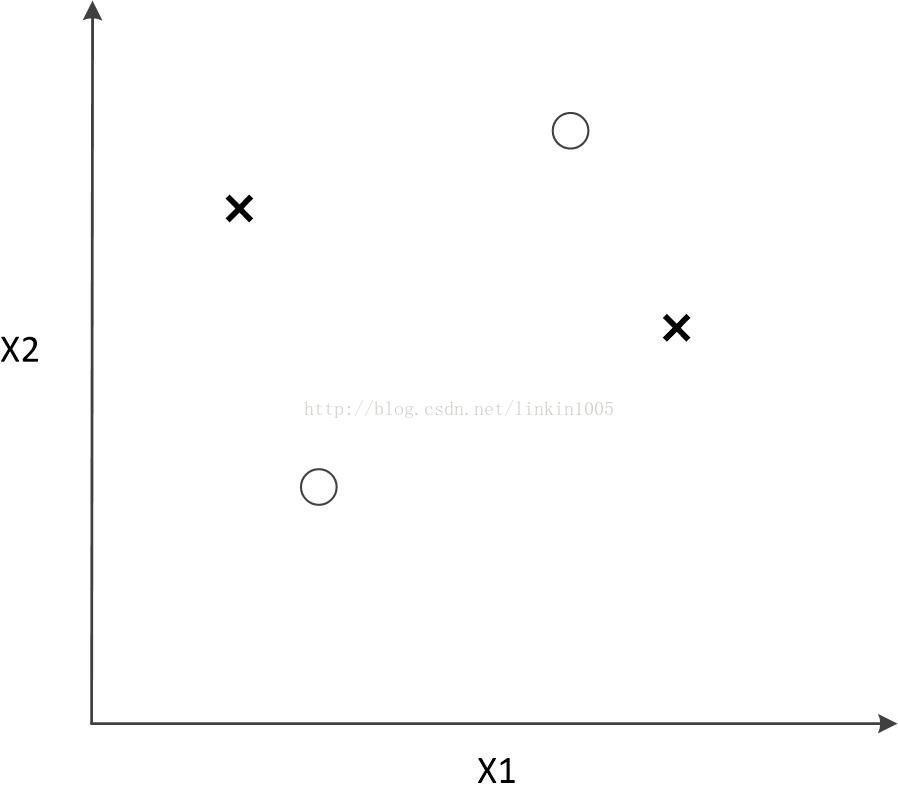
在討論線性迴歸時，我們用一次線性函式對訓練樣本進行擬合（如圖1所示）；然而，我們可以通過二次多項式函式對訓練樣本進行擬合（如圖2所示），函式對樣本的擬合程式看上去更“好”；當我們利用五次多項式函式對樣本進行擬合（如圖3所示），函式通過了所有樣本，成為了一次“完美”的擬合。

圖3建立的模型，在訓練集中通過x可以很好的預測y，然而，我們卻不能預期該模型能夠很好的預測訓練集外的資料。換句話說，這個模型沒有很好的泛化能力。因此，模型的泛化誤差(generalization error)不僅包括其在樣本上的期望誤差，還包括在訓練集上的誤差。

圖1和圖3中的模型都有較大的泛化誤差，然而他們的誤差原因卻不相同。圖1建立了一個線性模型，但是該模型並沒有精確的捕捉到訓練集資料的結構，我們稱圖1有較大的偏倚（bias）

，也稱欠擬合；圖3通過5次多項式函式很好的對樣本進行了擬合，然而，如果將建立的模型進行泛化，並不能很好的對訓練集之外資料進行預測，我們稱圖3有較大的，也稱過擬合。
通常，在偏倚和方差之間，這樣一種規律：如果模型過於簡單，其具有大的偏倚，而如果模型過於複雜，它就有大的方差。調整模型的複雜度，建立適當的誤差模型，就變得極其重要了。

二、預備知識

首先我們先介紹兩個非常有用的引理：

引理1：一致限（the union bound）令為k個不同的事件（不一定相互獨立），那麼有：

一致限說明：k個事件中任一個事件發生的概率小於等於這k個事件發生的概率和（等號成立的條件為這k個事件相兩兩互斥）。

引理2：Hoeffding 不等式（Hoeffding inequality）

令為m個獨立同分布的隨機變數，由引數為 的伯努利分佈（即）生成。令，為這些隨機變數的均值，對於任意有：

在機器學習中，引理2稱為Chernoff邊界（Chernoff bound）,它說明：假設我們用隨機變數的均值去估計引數，估計的引數和實際引數的差超過一個特定數值的概率有一確定的上界，並且隨著樣本量m的增大，與很接近的概率也越來越大。

通過以上兩個引理，我們能夠引出機器學習中很重要結論。
為簡單起見，我們只討論二分類問題，即類標籤為 。

假設給定的訓練集為，且各訓練樣本獨立同分布，皆為某個特定分佈D生成。對於一個假設函式（hypothesis），定義訓練誤差（training error）

（也稱為經驗風險（empirical risk）或經驗誤差(empiriacal error)）為：

訓練誤差為模型在訓練樣本中的錯分類的比例，如果我們要強調是依賴訓練集的，也可以將其寫作。

我們再定義泛化誤差（generalization error）：

這裡得到的是一個概率，表示通過特定的分佈D生成的樣本（x，y）中的y與通過預測函式h(x)生成的結果不同的概率。

注意，我們假設訓練集的資料是通過某種分佈D生成的，我們以此為依據來衡量假設函式。這裡的假設有時稱為PAC(probablyapproximately correct)假設。

線上性分類中，假設函式中引數如何得來？其中一個方法就是調整引數，使得訓練誤差最小，即：

我們稱這樣的方法為經驗風險最小化（empirical risk mininmization，ERM），其中 ，基於ERM原則的演算法可視作最基本的學習演算法。線性迴歸和logistic迴歸都可以看作是遵守ERM的演算法。

我們定義假設類集合（hypothesis class）為所有假設函式的集合。例如線性分類問題中，，其為所有的（輸入的定義域），對應的線性決策邊界。

因此，ERM也可以認為是一組分類器的集合中，使得訓練誤差最小的那個分類器，即：

3.有窮集

我們定義假設類集合由k個假設類(hypotheses)構成。其中，為k個由至{0,1}的對映函式構成，ERM從集合中k個元素選擇使得訓練誤差最小。

為了確保和泛化誤差的差值是有上界的，即如果訓練誤差很小，那麼泛化誤差也不會太大，我們需要完成兩個步驟：首先，證明對於任意h，是對的可靠估計；其次，證明存在上界。

我們令，隨機變數Z服從伯努利分佈，樣本由分佈生成：即：。並且定義：，即Z為指示變數，用來標記被假設函式錯誤分類的樣本。

泛化誤差定義為隨機變數Z的期望，訓練誤差為訓練樣本被假設函式誤分類的比例，即：

利用Hoeffding不等式，可以得到：

從上式可以看出，對於特定的的，當m很大時，訓練誤差和泛化誤差很接近的概率很大。但是，我們不僅僅需要考察對於特定的 ，訓練誤差和泛化誤差的接近程度，而是需要驗證對於所有的不等式也成立。

現令代表事件，對於任意，存在，因此，由引理1可得：

也可以得到他的等價式：

上式表示了假設集內任意假設函式的訓練誤差和泛化誤差的的接近程度小於一個常數的概率有下界，並且隨著樣本量的增加，訓練誤差接近泛化誤差的概率隨之增大。上式的結果稱為一致收斂。下面以此不等式引出個推論：

樣本量下界：
以上的不等式有三個元素：樣本量m，誤差閾值和概率，通過任意兩個元素，可以確定第三個元素。例如，我們可以關心下列問題：如果給定和，我們需要多大的樣本量才能保證訓練誤差和泛化誤差相差不超過的概率最小為？令可以解出m：

上面的不等式確定了一個m的下界，該下界稱為演算法的樣本複雜度（algorithm’s sample complex），也就是說，如果我們想通過樣本對總體有個較為準確的估計，我們需要採集最小的樣本量是多少。
誤差界限：

如果我們固定m和的值，求解，可以得到：

假設一致收斂成立，那麼對於所有，有，那麼，可以得到樣本泛化誤差和總體泛化誤差的距離：

令 ，，即h*表示在集合中使得泛化誤差最小的那個假設函式。那麼有：

上式第一行不等式依據的是和，不等式第二行是由是對樣本最小的誤差的假設函式，因此小於 ，第三行是根據不等式。從不等式可以看出，對於（即利用訓練集得到的假設函式）的泛化誤差在任何情況下也不會比最理想的泛化誤差多。結合前面的結論，我們可以得到定理1：

定理1：令，且m和值固定，在誤差小於一個閾值的概率為至少為的情形下，有：

定理1給出了一個很重要的結論：如果我們擴充假設類集合的範圍，即由原來的假設類擴充為即，則上式第一項（可以非正式的視其為偏差）的值會變小，因為擴充假設類集，可能有更好的假設函式使得最小泛化誤差下降；第二項（可以非正式的視其為方差）的值會增大，因為k的值增加了。因此，如果假設類過小，則第一項過大，會造成欠擬合，通過擴充假設類，可以使得第一項的值下降，但是第二項值上升，如果擴充過大，會造成過擬合，同樣會增加泛化誤差。因此要想得到最小的泛化誤差，需要在選擇合適的，即在方差和偏差之間進行權衡。

假如固定和，去求解m，我們可以得到一條關於樣本複雜度的推論：

推論1：令，和為定值，再令的概率不低於，那麼樣本量需滿足：

4.無窮集

前一節我們介紹了在假設類集合是有窮集的情況下泛化誤差、訓練誤差和樣本量之間的關係。然而，存在很多以實數為引數的模型，假設類集合中元素數量是無窮的（如線性分類問題）。我們將如何處理？

下面以線性分類為例，假設分類的決策邊界由線性函式表示，且該線性函式有d個實數引數。如果我們用計算機表示這些實數，根據IEEE雙精度浮點數的標準，用64位二進位制表示一個實數，那麼，這d個實數需要用64d個2進位制位表示，因此，這裡假設類集合最多由個元素構成。由推論1可得，如果需要保證的概率不小於，需滿足，因此可以看出，訓練樣本量和模型引數數量為線性關係。事實上，依賴64位浮點數無法得出準確的引數，然而， 如果我們嘗試去最小化訓練誤差，也會得出理想的假設函式。

前文的結論是依賴於的引數設定。如線上性分類器中 ，此處有n+1個引數。如果這樣定義分類器：，此時有2n+2個引數，但是這二者定義了相同的：在n維空間的線性分類器。

最後通過引入VC維的概念，將誤差理論推廣到更加一般的情形：

VC維

給定一個集合；，,這d個點可以用種方法正負樣本。如果存在可以將這種標記的情況都能夠有效分類，我們就稱可以雜湊（shatter）S。通過集合中的某個假設函式h，可以對這個點構成的任何情況進行無誤差的分類。將一個假設集能夠無誤差分類的最大的點的數量稱為改假設集的VC維，記作。

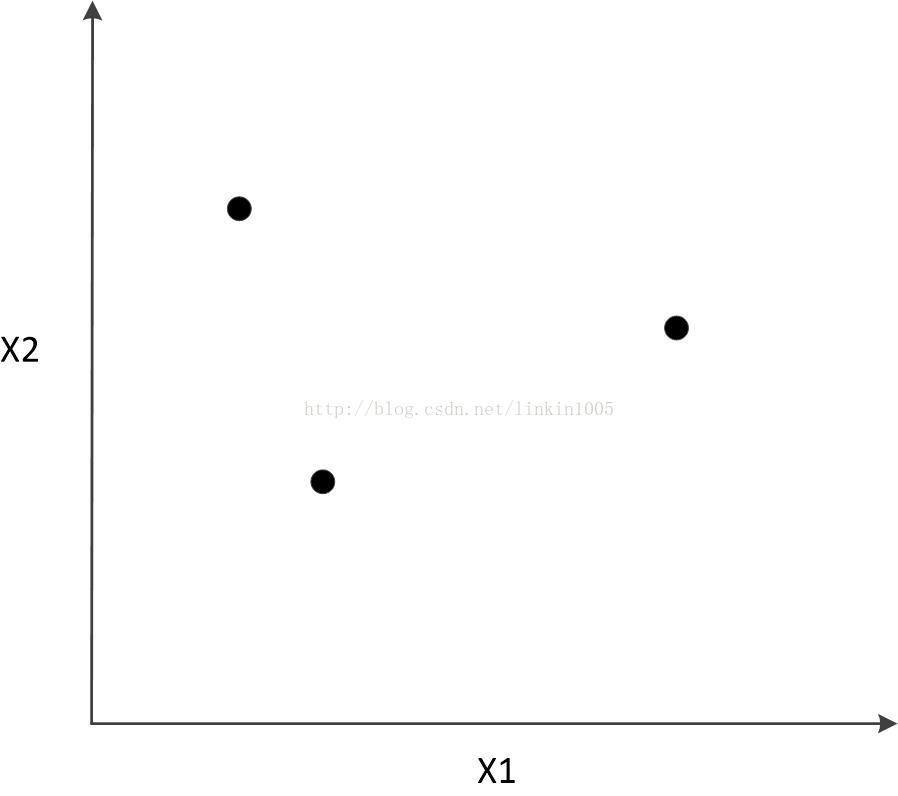
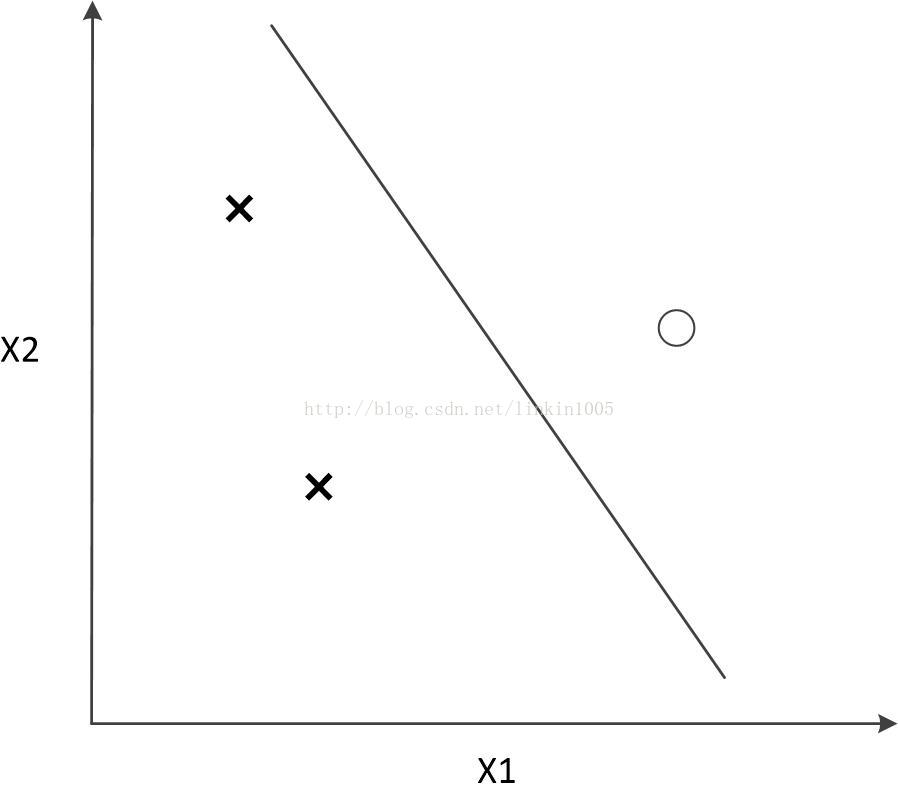
下面舉例說明，假設有三個點如下圖所示：

這三個樣本點有2³=8種分類可能，如果使用線性分類器對其進行分類，可以得到“零訓練誤差”，如下圖所示：

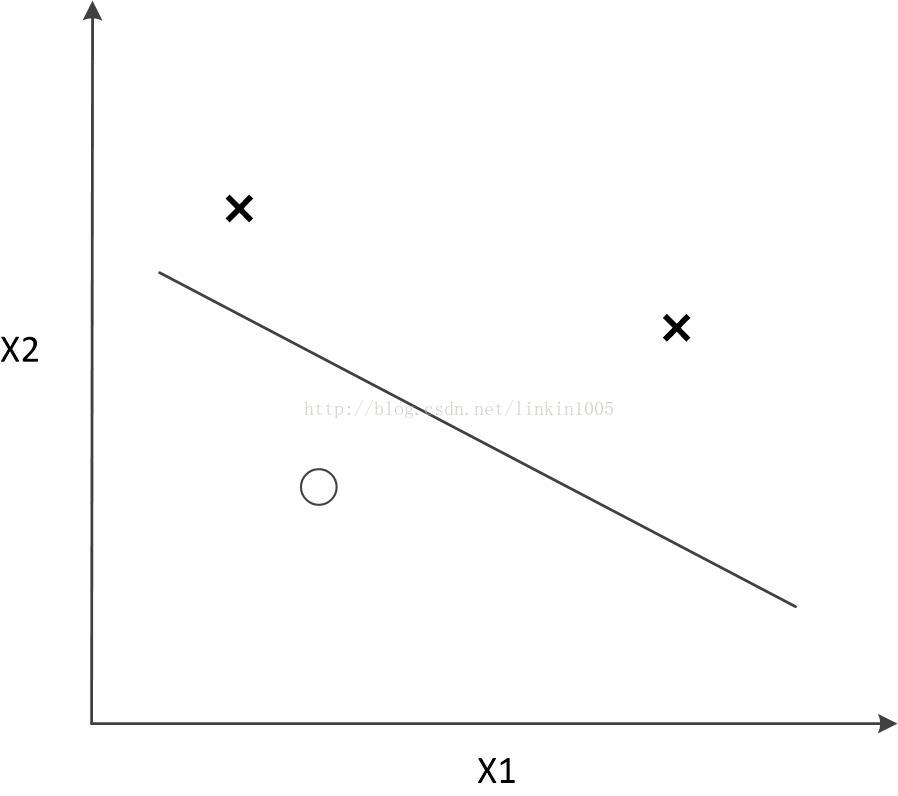
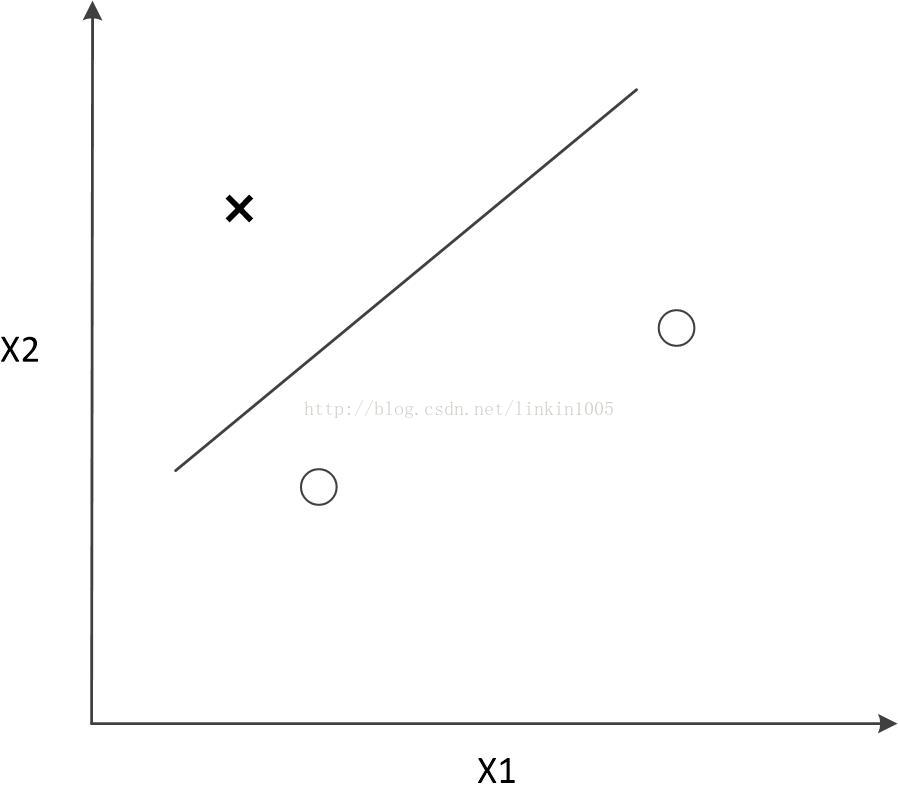
然而，線性分類器最多對3個點構成的所有可能分類情況進行無誤差分類。如果超過3個點線性分類器將無法進行分類。如下圖所示：

這裡的結論可能很悲觀，線性分類器在二維平面上至多隻能給3個點進行無誤差的分類。（更一般的，k維線性分類器最多隻能給k+1個點進行無誤差分類。）然而，實際的應用中，並不需要構建一個模型使得對於訓練集進行無誤差的分類，甚至分類過於精確，會使得模型的泛化能力變得很弱，因此VC維僅僅是保證理論的嚴密，以及可以相關證明的前提條件，並不能完全做為分類演算法準確程度的度量。
最後，介紹兩個重要的定理：

定理2：令為給定的假設集，且，在概率不小於的情況下，對於任意，有：

同樣有

也就是說，如果一個假設集，VC維是有限的，那麼，隨著m的增大，任意的訓練誤差和泛化誤差一致收斂。並且有如下推論：

推論2：假設且對於所有要確保其概率不低於，需滿足。

推論2的含義是，如果需要確保訓練誤差和泛化誤差的差值在一個給定的範圍內，並且發生的概率不低於，需要的樣本數量和假設集的VC維大小呈線性相關。

5.總結

本文給出了訓練誤差和泛化誤差的一般性定義；並介紹了ERM原則；證明了泛化誤差和訓練誤差間差距、樣本量和誤差概率之間的關係；最後通過引入VC維，推出了更一般的情況下他們之間的關係。