先了解下對極幾何，兩個相機在不同位置(實際要求光心位置不同即可)拍攝兩張圖，這個模型就是對極幾何，如下圖(摘自《計算機視覺中的多檢視幾何》)：
<img src="https://pic2.zhimg.com/98cb131413f8c6ea4a995a2b5f9ee741_b.jpg" data-rawwidth="338" data-rawheight="291" class="content_image" width="338">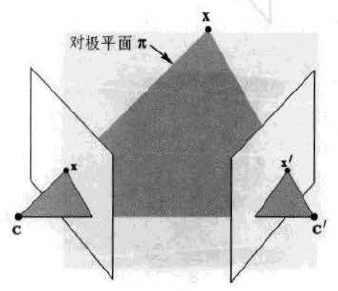
兩攝像機光心分別是C和C'，影象平面是兩白色的平面，空間中某一個點X在兩張圖的投影點分別是x和x'。這樣的模型就是對極幾何，空間點和兩光心組成的平面叫做對極面。簡言之，不同視點拍攝的兩個場景滿足對極幾何關係。

再講下基本矩陣，存在這麼一個矩陣F，使得空間中不在兩影象平面上的任意點X分別在兩影象的投影座標x,x'滿足等式(x')T*F*x=0，即x'的轉置乘以F，再乘以x的結果為0，那麼F就是左邊影象到右邊影象的基本矩陣，從公式上可以看出基本矩陣是有方向的，右圖到左圖的基本矩陣就是F的轉置。F矩陣有如下性質：
1、秩為2；
2、F矩陣是一個7個自由度的3*3矩陣(3*3矩陣本身9個自由度，因為相差一個常數因子和行列式值為0兩個條件，減掉2個自由度)，相差一個常數因此的意思是：kF(k!=0)也是基本矩陣，也就是說如果F是基本矩陣，那麼kF也是基本矩陣，所以基本矩陣不唯一，在相差一個倍數的前提下是唯一的，也就是我們可以固定矩陣中某一個非零元素的值，這樣自然少一個自由度。
這裡講下自己對基本矩陣的理解：很簡單，基本矩陣提供了三維點到二維的一個約束條件。舉個例子，現在假設我們不知道空間點X的位置，只知道X在左邊圖上的投影x的座標位置，也知道基本矩陣，首先我們知道的是X一定在射線Cx上，到底在哪一點是沒法知道的，也就是X可能是Cx上的任意一點(也就是軌跡的意思)，那麼X在右圖上的投影肯定也是一條直線。也就是說，如果我們知道一幅影象中的某一點和兩幅圖的基本矩陣，那麼就能知道其對應的右圖上的點一定是在一條直線上，這樣就約束了兩視角下的影象中的空間位置一定是有約束的，不是任意的。基本矩陣是很有用的一個工具，在三維重建和特徵匹配上都可以用到。

最後帶下本質矩陣，本質矩陣就是在歸一化影象座標下的基本矩陣。不僅具有基本矩陣的所有性質，而且還可以估計兩相機的相對位置關係，具體內容可參考《計算機視覺中的多檢視幾何》。