複習數學1的線性代數，矩陣相乘這塊有點暈，想編個C++物件化的矩陣相乘小程式……

相乘部分

void sum(juzhen a, juzhen b, juzhen &c)
{
	int s=0;
	for (int i = 1; i <= a.m1(); i++)//A矩陣的M
		for (int j = 1; j <= b.n1(); j++)//B矩陣的S
		{
			for (k0 = 1; k0 <= a.n1(); k0++)//a.n1也就是b.m1(a的n，b的n)【行向量*列向量】
			{
				s += a.read(i,k0)*b.read(k0,j);
			}
				c.write(i, j, s);
				s = 0;
		}
}
 

程式碼中的頭兩個for迴圈就是i，j的。公式中的k從1到p求和就是裡面的k0的for迴圈。

容易出現誤解的就是公式中只是表示第“[i][j]”元素，而不是整個矩陣，整個矩陣的結果需要外面的兩個for迴圈。

本質：這就是個p維向量（高中就記2維）的兩向量相乘公式而已【結果為數，是新矩陣的一個元素】

可執行程式碼：

#include<iostream>
#include <string>
using namespace std;

class juzhen
{
private:
	int m,n;//長寬
	int num[10][10] = {0};
	string name;

public:
	 void size(int a,int b)
	 {	m = a;
		n = b; }
	 void set()
	 {
		 cout << "此矩陣規模：" << this->m <<"，"<< this->n << endl;//=====？
		 for (int i = 1; i <= this->m; i++)
			 for (int j = 1; j <= this->n; j++)
			 {
				 cin >> this->num[i][j];
			 }
		 cout << "輸入完成"<< endl;
	 }
	 void display()
	 {
		 for (int i = 1; i <= this->m; i++)//===i為行號（第幾行），j為列號
			 for (int j = 1; j <= this->n; j++)
			 {
				 cout << this->num[i][j] << " ";
				if (j == this->n) cout << endl;//先輸出再換行
			 }
	 }
	 int read(int a, int b) { return num[a][b]; }//呼叫此函式，得[m][n]元素的值
	 void write(int a, int b,int count) {  num[a][b]=count; }//第三個引數的值，傳遞給[a][b]元素
	 int m1() { return m; }//呼叫得到矩陣的m
	 int n1() { return n; }//呼叫得到矩陣的n
};

int m0, n0, s0, k0;//矩陣規模（容易搞混的東西）

void sum(juzhen a, juzhen b, juzhen &c)//矩陣相乘公式所在。。。【要改實參值的要用&引用】
{
	for (int i = 1; i <= a.m1(); i++)//A矩陣的M
		for (int j = 1; j <= b.n1(); j++)//B矩陣的S
		{

			int s = 0;
			for (k0 = 1; k0 <= a.n1(); k0++)//a.n1也就是b.m1(a的n，b的n)【行向量*列向量】
			{
				s += a.read(i,k0)*b.read(k0,j);//因為用了C++，所以沒那麼直觀，就是a[i][k]*b[k][j]，套個for迴圈求累加和（就是高中時向量的點乘）
			}
				c.write(i, j, s);
		}
}
int main()
{
	juzhen A,B,C;
	cout << "設定m,s,n。A的m*s,B的s*n(橫條數*縱條數)"<<endl;
	cin >> m0>> s0>> n0;
	A.size(m0, s0);
	B.size(s0, n0);

	C.size(m0, n0);

	A.set();
	B.set();

	sum(A, B, C);//C=A*B
	cout << "結果C的m*n：" << endl;
	C.display();

	return 0;
}
 

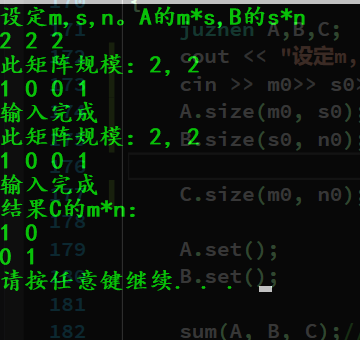
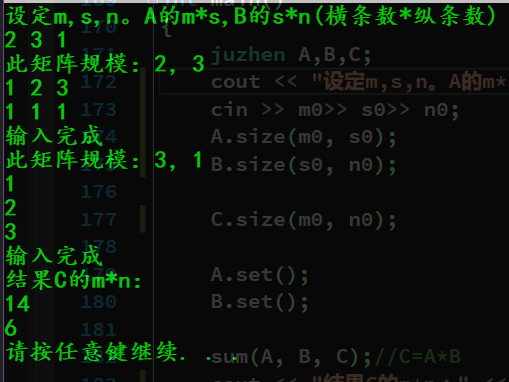
樣例輸入及輸出：

懶得打了……就如圖所示兩個矩陣

PS：函式中形參引用真好用，過去一直不知道，省得用指標了。（不然改不了C矩陣的實際元素值）

void sum(juzhen a, juzhen b, juzhen &c)//矩陣相乘公式所在。。。【要改實參值的要用&引用】