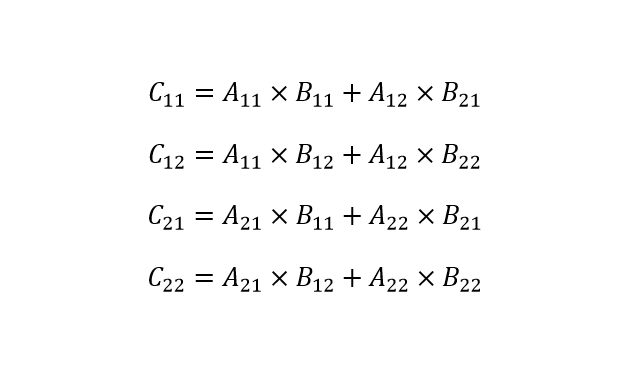一個簡單的分治演算法求矩陣相乘
C=A * B ，假設三個矩陣均為n×n，n為2的冪。可以對其分解為4個n/2×n/2的子矩陣分別遞迴求解：

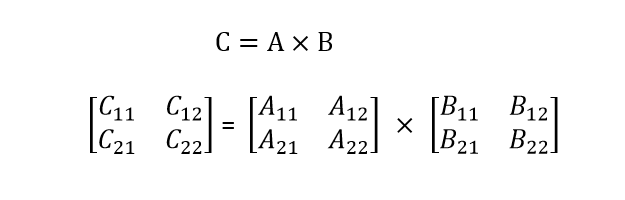
遞迴分治演算法：

演算法中一個重要的細節就是在分塊的時候，採用的是下標的方式。

#include <stdio.h>
#include <stdlib.h>
#define ROW 16       //指定 行數
#define COL 16       //指定 列數 

int a[ROW][COL],b[ROW][COL];  //矩陣a 和 矩陣b
int **c;                      // c = a * b 
 


//儲存一個矩陣的第一個元素的位置，即左上角元素的下標
//如果加上一個長度就可以知道整個矩陣了
typedef struct {   //這裡沒有指定一個矩陣的長度，在分塊時應該加入長度，否則不知道子塊矩陣的大小
    int str,stc;    //str行下標  ； strc列下標
}subarr;

// 兩矩陣arr、brr相加減 儲存在temp中
void operate(int **arr,int **brr,subarr te,char op,int **temp,int len);

//分治法 求矩陣相乘 ，sa,sb分別為矩陣a,b參加運算的首元素
int ** square_recursive(subarr sa,subarr sb,subarr sc,int
 
 len){
    int n=len;
    int **temp;
    int i;
    // 申請一個臨時矩陣，用於儲存a*b 
    temp=(int**)malloc(sizeof(int *)*n);
    for ( i=0;i<n;++i){
        temp[i]=(int *)malloc(sizeof(int)*n);
    }
    // 長度為1 則直接相乘
    if (n==1)
    {
        temp[0][0]=a[sa.str][sa.stc]*b[sb.str][sb.stc];
    }else{
         // 這裡都是對下標進行初始化
 

         // sa,sb,sc代表輸入矩陣A,B,temp參加運算的首元素下標，因為進行分塊後只進行特定子塊的運算
         //標號1，2，3，4 分別代表第一、二、三、四個子塊
        subarr sa1,sb1, sc1;
        subarr sa2,sb2, sc2;
        subarr sa3, sb3,sc3;
        subarr sa4, sb4, sc4;
        // 矩陣A 進行分塊後的各個子塊下標
        sa1.str=sa.str;
        sa1.stc=sa.stc;
        sa2.str=sa.str;
        sa2.stc=sa.stc+n/2;
        sa3.stc=sa.stc;
        sa3.str=sa.str+n/2;
        sa4.str=sa.str+n/2;
        sa4.stc=sa.stc+n/2;
        // 矩陣B 進行分塊後的各個子塊下標
        sb1.str=sb.str;
        sb1.stc=sb.stc;
        sb2.str=sb.str;
        sb2.stc=sb.stc+n/2;
        sb3.stc=sb.stc;
        sb3.str=sb.str+n/2;
        sb4.str=sb.str+n/2;
        sb4.stc=sb.stc+n/2;
        // 矩陣temp 進行分塊後的各個子塊下標
        sc1.str=sc1.stc=0;
        sc2.str=0;
        sc2.stc=n/2;
        sc3.stc=0;
        sc3.str=n/2;
        sc4.str=n/2;
        sc4.stc=n/2;
// 將矩陣分為四塊  分別求解。採用下標的方式進行分塊，可以省去複製矩陣所產生的時間
// 若要複製矩陣則會產生 O(n*n)的時間複雜度
    operate(square_recursive(sa1,sb1,sc1,n/2),square_recursive(sa2,sb3,sc1,n/2),sc1,'+',temp,n/2);

        operate(square_recursive(sa1,sb2,sc2,n/2),square_recursive(sa2,sb4,sc2,n/2),sc2,'+',temp,n/2);

        operate(square_recursive(sa3,sb1,sc3,n/2),square_recursive(sa4,sb3,sc3,n/2),sc3,'+',temp,n/2);

        operate(square_recursive(sa3,sb2,sc4,n/2),square_recursive(sa4,sb4,sc4,n/2),sc4,'+',temp,n/2);


    }
    return temp;

}
//  temp矩陣的te位置（四個子塊中的一個）=arr+brr
// len表示arr，brr參加運算的長度
// op是運算子 ‘+’ 
void operate(int **arr,int **brr,subarr te,char op,int **temp,int len){
    int i,j;
    switch(op){
        case '+':
            for (i=0;i<len;++i){
                for (j = 0; j < len; ++j)
                {
                    temp[te.str+i][te.stc+j]=arr[i][j]+brr[i][j];
                }
            }
            break;
        case '-':
            for (i=0;i<len;++i){
                for (j = 0; j < len; ++j)
                {
                    temp[te.str+i][te.stc+j]=arr[i][j]-brr[i][j];
                }
            }
            break;
    }
}
//為矩陣初始化 即賦值
void createarr(int temp[][COL]){
    int i,j;
    for (i = 0; i < ROW; ++i)
    {
        for (j = 0; j < COL; ++j)
        {
            temp[i][j]=(int)rand()%5;

        }

    }

}
// 列印C矩陣
void print(){
    int i,j;
    printf("\n====================================\n");
    for (i = 0; i < ROW; ++i)
    {
        for (j = 0; j < COL; ++j)
        {
            printf("%d\t", c[i][j]);
        }
        printf("\n");
    }
    printf("===================================\n");
}
// 列印矩陣
void printarray(int a[ROW][COL]){
    int i,j;
    printf("-----------------------\n");
    for (i = 0; i < ROW; ++i)
    {
        for (j = 0; j < COL; ++j)
        {
            printf("%d \t", a[i][j]);
        }
        printf("\n");
    }
    printf("-----------------------\n");
}


int main(){
    int i,j;
    subarr sa,sb,sc;
    int len;
    //初始化各個下標
    sa.str=sa.stc=0;
    sb.str=sb.stc=0;
    sc.str=sc.stc=0;
    // 長度賦值，因為在subarr結構裡沒有長度的定義
    len=ROW;
    //申請空間
    c=(int**)malloc(sizeof(int *)*len);
    for (i=0;i<len;++i){
        c[i]=(int *)malloc(sizeof(int)*len);
    }
    // 給矩陣A，B 複製初始化
    createarr(a);
    createarr(b);
    //  進行運算
    c=square_recursive(sa,sb,sc,len);
    // 列印矩陣A,B,C
    printarray(a);
    printarray(b);
    print();
    return 0;
}

=========== 王傑 原創作品轉載請註明出處==============