假設我們給出了兩條曲線y=f(x),yg(x)，如圖1所示，在x=a,b處有交點並且在區間[a,b]內第一條曲線位於第二條的上方，為了求出曲線之間的面積，很自然地想法是使用如圖所示垂直的細條。在x處的高度為低點的曲線與高點之間的距離f(x)−g(x)，其底是dx。因此，面積的單元是

dA=[f(x)−g(x)]dx

總面積為

A=∫dA=∫ba[f(x)−g(x)]dx(1)

我們將較小的a設為積分下限，將b設為上限來計算積分值。這樣的話增量(或者說微分)dx將一直是正的。另外還應該指出，當x=a,b時，兩個函式產生相同的y值；也就是說，他們是方程f(x)=g(x)的解。為了找到它們，我們需要求解這個方程。

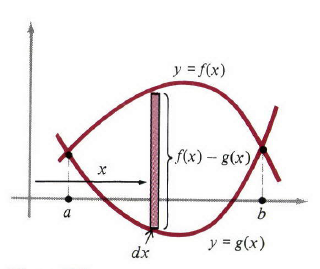
圖1

我們建議大家不要靠死記硬背記住公式(1)，並且機械的將它套用到面積問題上。我們的目標是掌握這個方法，利用幾何思想與對問題從無到有的構造出所需公式都是為了達到這個目標。該方法同樣適用於水平窄帶，往往這樣做會更方便。在這種情況下，窄帶的寬度將是dy，總面積將通過對y積分得到。

作為大家的輔助手段，對用積分求面積的方法，我們列出了它所遵循的大綱：

1. 畫出要求的面積區域，在圖上寫下邊界曲線的方程並找到他們的交點。
2. 確定用垂直窄帶(寬為dx)還是水平窄帶(寬為dy)，在圖中畫出一條窄帶。
3. 著影象並利用曲線邊界的方程，寫下窄帶面積dA，也就是長和寬的乘積。將dA完全用變數(x 或y
   )表示出來。
4. 在x或y的上下限之間積分dA，上下限可以通過檢查影象得到。

例1：曲線y=x2,y=4的邊界圍成的區域如圖2所示，如果我們選用垂直窄帶，那麼它的長度為4−x2，面積為dA=(4−x2)dx。整個區域的面積為

∫22(4−x2)dx=4x−13x3∣∣2−2=(8−83)−(−8+83)=323

我們建議大家儘可能使用對稱來簡化計算。在這種情況下，影象左右對稱，所以我們只需計算從x=0到x=2之間的積分，它是面積的一半，然後乘以2就得到總面積：

2∫20(4−x2)dx=2(4x−13x3)∣∣20=2(8−83)=323

正如計算展示的那樣，這樣做有一個好處，就是一個積分的極限是0。

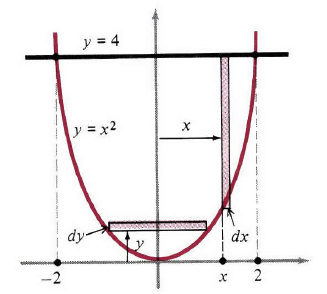
圖2

如果我們決定用水平窄帶，那麼長度就是右端的x值減去左端的x值。即y√−−y√，所以dA=[y√−(−y√)]dy=2y√dy，整個面積是

∫402y√dy=43y3/2∣∣40=323

答案跟以前一樣，這並不奇怪，但不管這樣令人放心。

我們曾經強調過好的影象對理解以及執行這些過程是多麼重要。

例2：曲線y=3−x2,y=