前面的文章中，我們完成了兩個主要目的。首先，我們將面積近似為給定曲線下的面積，並利用他們和的極限求出確切的面積值。第二，通過使用更強大的方法微積分基本定理，我們學會了如何計算極限的數值解。幾乎前幾篇文章的整個內容可以被壓縮成下面的命題：如果f(x)在[a,b]上是連續的，那麼

其中F(x)是f(x)的任何一個不定積分。

在幾何和物理中有許多其他量本質上可以用相同的方法來處理，例如體積、弧長、表面積和一些基本物理量。每種情況的處理過程都是相同的：獨立變數的區間被劃分成小的子區間，求解量用某種對應的和來近似，這些和的極限用定積分的形式得到確切值，它可以用基本定理來評估。

在求解曲線下面積的過程中，我們已經知道了極限和的細節，這就是前面文章講到的。我們沒有必要對所有遇到的量都考慮這些細節。所需要的符號既複雜又重複，阻礙了我們對它的直觀理解。

本著這種精神，我們將其簡化為圖1的形式，並用簡單與直觀的方式來重建(1)中定積分的定義。我們認為曲線下的面積是由許多細長的垂直矩形組成的。在圖中，典型的就是高為y寬為dx的窄帶，因此面積為

其中y=f(x)。這個面積叫做面積的微分單元，或者簡稱為面積的單元；它可以是區域的任何一個位置，只要確保x是a,b 之間的值即可。現在我們將區域面積A看做這些面積單元dA的總和。這個加法用符號表示就是

因為面積單元穿過了a到b的所有區域，我們可以將(3)表示成更準確的形式

(4)中的最後一步我們得到了定積分，此時寫出積分變數和積分極限。用這種方式我們省掉了繁瑣的細節，直接得到面積的定積分，而且一點都不用考慮和的極限。

從這個角度來看，積分就是一個數值，我們可以將它分成很多個方便的小塊，然後再將他們全部加起來即可。這就是積分過程的直觀萊布尼茨方法，我們將在下篇文章中詳細說明和加強對它的理解。

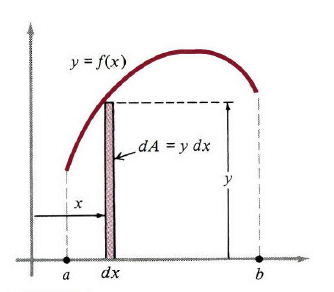
圖1