Problem Description
cjj is fun with math problem. One day he found a Olympic Mathematics problem for primary school students. It is too difficult for cjj. Can you solve it?

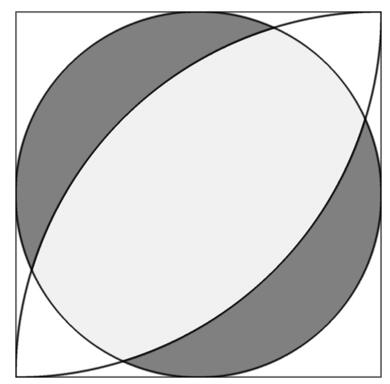
Give you the side length of the square L, you need to calculate the shaded area in the picture.

The full circle is the inscribed circle of the square, and the center of two quarter circle is the vertex of square, and its radius is the length of the square.

Input
The first line contains a integer T(1<=T<=10000), means the number of the test case. Each case contains one line with integer l(1<=l<=10000).

Output
For each test case, print one line, the shade area in the picture. The answer is round to two digit.

Sample Input

1
1

Sample Output

0.29

Author
BUPT

Source
2016 Multi-University Training Contest 10

題意：給你正方形的邊長，求陰影部分的面積。。。
解法：中間那個圓的非陰影部分就是。3個圓的的面積交。。所以陰影部分的面積就是圓的面積-3個圓的交面積。。。

#include<bits/stdc++.h>
using namespace std;

const double eps=1e-8;
int cmp(double x){
    if(fabs(x)<eps) return 0;
    if(x>0) return 1;
    return
 
 -1;
}
const double pi=acos(-1.0);
inline double sqr(double x){
    return x*x;
}
struct point{
    double x,y;
    point(){};
    point(double a,double b):x(a),y(b){};
    void input(){
        scanf("%lf %lf",&x,&y);
    }
    friend point operator + (const point &a,const point &b){
        return point(a.x+b.x,a.y+b.y);
    }
    friend point operator - (const point &a,const point &b){
        return point(a.x-b.x,a.y-b.y);
    }
    friend bool operator == (const point &a,const point &b){
        return cmp(a.x-b.x)==0&&cmp(a.y-b.y)==0;
    }
    friend point operator * (const point &a,const double &b){
        return point(a.x*b,a.y*b);
    }
    friend point operator * (const double &a,const point &b){
        return point(a*b.x,a*b.y);
    }
    friend point operator / (const point &a,const double &b){
        return point(a.x/b,a.y/b);
    }
    double norm(){
        return sqrt(sqr(x)+sqr(y));
    }
};
double det(const point &a,const point &b){
    return a.x*b.y-a.x*b.y;
}
double dot(const point &a,const point &b){
    return a.x*b.x+a.y*b.y;
}
double dis(const point &a,const point &b){
    return (a-b).norm();
}
point rotate_point(const point &p,double A){
    double tx=p.x,ty=p.y;
    return point(tx*cos(A)-ty*sin(A),tx*sin(A)+ty*cos(A));
}
int dcmp(double k){
    return k<-eps?-1:k>eps?1:0;
}
double cross(const point &a,const point &b){
    return a.x*b.y-a.y*b.x;
}
double abs(const point &o){
    return sqrt(dot(o,o));
}
struct Circle{
    point p;
    double r;
    bool operator < (const Circle &o) const{
        if(dcmp(r-o.r)!=0) return dcmp(r-o.r)==-1;
        if(dcmp(p.x-o.p.x)!=0){
            return dcmp(p.x-o.p.x)==-1;
        }
        return dcmp(p.y-o.p.y)==-1;
    }
    bool operator == (const Circle &o) const{
        return dcmp(r-o.r)==0&&dcmp(p.x-o.p.x)==0&&dcmp(p.y-o.p.y)==0;
    }
};

//圓的交面積
double area(Circle &x,Circle &y){
    double a=dis(x.p,y.p),b=x.r,c=y.r;
    double cta1=acos((a*a+b*b-c*c)/2/(a*b)),
           cta2=acos((a*a+c*c-b*b)/2/(a*c));
    double s1=b*b*cta1-b*b*sin(cta1)*(a*a+b*b-c*c)/2/(a*b);
    double s2=c*c*cta2-c*c*sin(cta2)*(a*a+c*c-b*b)/2/(a*c);
    return s1+s2;
}

//圓的面積並。
point rotate(const point &p,double cost,double sint){
    double x=p.x,y=p.y;
    return point(x*cost-y*sint,x*sint+y*cost);
}
pair<point,point> crosspoint(point ap,double ar,point bp,double br){
    double d=(ap-bp).norm();
    double cost=(ar*ar+d*d-br*br)/(2*ar*d);
    double sint=sqrt(1.0-cost*cost);
    point v=(bp-ap)/(bp-ap).norm()*ar;
    return make_pair(ap+rotate(v,cost,-sint),ap+rotate(v,cost,sint));
}
inline pair<point ,point> crosspoint(const Circle &a,const Circle &b){
    return crosspoint(a.p,a.r,b.p,b.r);
}
Circle tc[10]; //待求圓
int m;         //待求圓的個數
struct Node{
    point p;
    double a;
    int d;
    Node(const point &p,double a,int d):p(p),a(a),d(d){};
    bool operator <(const Node &o)const{
        return a<o.a;
    }
};
double arg(point p){
    return arg(complex<double>(p.x,p.y));
}
double solve(){   //返回並面積
    int n=0;
    Circle c[10];
    sort(tc,tc+m);
    m=unique(tc,tc+m)-tc;
    for(int i=m-1;i>=0;--i){
        bool ok=true;
        for(int j=i+1;j<m;j++){
            double d=(tc[i].p-tc[j].p).norm();
            if(dcmp(d-abs(tc[i].r-tc[j].r))<=0){
                ok=false;
                break;
            }
        }
        if(ok) c[n++]=tc[i];
    }
    double ans=0;

    for(int i=0;i<n;i++){
        vector<Node>event;
        point boundary=c[i].p+point(-c[i].r,0);
        event.push_back(Node(boundary,-pi,0));
        event.push_back(Node(boundary,pi,0));
        for(int j=0;j<n;++j){
            if(i==j) continue;
            double d=(c[i].p-c[j].p).norm();
            if(dcmp(d-(c[i].r+c[j].r))<0){
                pair<point,point> ret=crosspoint(c[i],c[j]);
                double x=arg(ret.first-c[i].p);
                double y=arg(ret.second-c[i].p);
                if(dcmp(x-y)>0){
                    event.push_back(Node(ret.first,x,1));
                    event.push_back(Node(boundary,pi,-1));
                    event.push_back(Node(boundary,-pi,1));
                    event.push_back(Node(ret.second,y,-1));
                }
                else{
                    event.push_back(Node(ret.first,x,1));
                    event.push_back(Node(ret.second,y,-1));
                }
            }
        }
        sort(event.begin(),event.end());
        int sum=event[0].d;
        for(int j=1;j<(int)event.size();++j){
            if(sum==0){
                ans+=cross(event[j-1].p,event[j].p)/2;
                double x=event[j-1].a;
                double y=event[j].a;
                double area=c[i].r*c[i].r*(y-x)/2;
                point v1=event[j-1].p-c[i].p;
                point v2=event[j].p-c[i].p;
                area-=cross(v1,v2)/2;
                ans+=area;
            }
            sum+=event[j].d;
        }
    }
    return ans;
}
int main(){

    int t;
    scanf("%d",&t);
    while(t--){
        double n;
        Circle a,b,c;
        scanf("%lf",&n);
        a.p.x=(n/2);
        a.p.y=n/2;
        a.r=n/2;

        b.p.x=n;
        b.p.y=0;
        b.r=n;

        c.p.x=0;
        c.p.y=n;
        c.r=n;
        double temp=2*pi*(n/2)*(n/2)-area(a,b)-area(a,c);
        printf("%.2f\n",temp);
    }
    return 0;
}