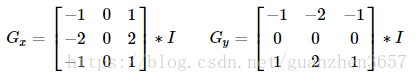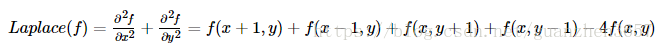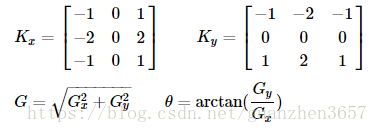opencv學習--opencv內的6種影象邊緣檢測演算法的實現
如上篇部落格所述,影象邊緣檢測演算法主要有Sobel, Scarry, Canny, Laplacian,Prewitt, Marr-Hildresh,現在進行總結
1.Sobel運算元
Sobel運算元是主要用於邊緣檢測的離散微分運算元,它結合了高斯平滑和微分求導,用於計算影象灰度函式的近似梯度
假定輸入影象矩陣為 I,卷積核大小為 3x3,則水平一階導數 Gx 和垂直一階導數 Gy 分別為:
輸出的影象矩陣 G 為:
opencv中sobel函式的引數如下
void cv::Sobel ( InputArray src, // 輸入影象 OutputArray dst, // 輸出影象 int ddepth, // 輸出影象深度,-1 表示等於 src.depth() int dx, // 水平方向的階數 int dy, // 垂直方向的階數 int ksize = 3, // 卷積核的大小,常取 1, 3, 5, 7 等奇數 double scale = 1, // 縮放因子,應用於計算結果 double delta = 0, // 增量數值,應用於計算結果 int borderType = BORDER_DEFAULT // 邊界模式 )
因為Sobel運算元結合了高斯平滑和分化,因此結果會具有更多的抗噪性。
#include<opencv2\opencv.hpp> #include<opencv2\highgui\highgui.hpp> using namespace std; using namespace cv; //邊緣檢測 int main() { Mat img = imread("lol3.jpg"); imshow("原始圖", img); Mat grad_x, grad_y; Mat abs_grad_x, abs_grad_y, dst; //求x方向梯度 Sobel(img, grad_x, CV_16S, 1, 0, 3, 1, 1,BORDER_DEFAULT); convertScaleAbs(grad_x, abs_grad_x); imshow("x方向soble", abs_grad_x); //求y方向梯度 Sobel(img, grad_y,CV_16S,0, 1,3, 1, 1, BORDER_DEFAULT); convertScaleAbs(grad_y,abs_grad_y); imshow("y向soble", abs_grad_y); //合併梯度 addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, dst); imshow("整體方向soble", dst); waitKey(0); }
2. Scarry
Scarry演算法實際上是opencv中sobel運算元的特殊改進情況。當核心大小為3時,Sobel核心可能產生比較明顯的誤差,為了解決這一問題,Opencv提供了Scharr函式,但該函式僅作用於大小為3的核心,該函式的運算與Sobel函式一樣快,但結果卻更加精確。
使用Scharr濾波器運算子計算x或y方向的影象差分。其實它的引數變數和Sobel基本上是一樣的,除了沒有ksize核的大小。
void Scharr(inputArray,outputArray,int ddepth,int dx,int dy,double scale=1,double delta=0,int borderType=BORDER_DEFAULT)
*第一個引數,輸入影象。
*第二個引數,輸出影象。
*第三個引數,輸出影象深度。
*第四個引數,x方向上的差分階數。
*第五個引數,y方向上的差分階數。
*第六個引數,計算導數值時可選的縮放因子,預設值1,表示預設情況下沒用應用縮放。
*第七個引數,表示在結果存入輸出影象之前可選的delta值,預設值0。
*第八個引數,邊界模式。
程式套用sobel的即可
3. laplace
索貝爾運算元 (Sobel) 和拉普拉斯運算元 (Laplace) 不同之處在於,前者是求一階導,後者是求二階導。
Laplacian運算元是n維歐幾里德空間中的一個二階微分運算元,定義為梯度grad的散度div。由於Laplacian使用了影象梯度,它內部的程式碼其實是呼叫了Sobel運算元的。
Laplacian運算元是二階微分運算元。凡是二階運算元對噪聲都比較敏感,在使用前要進行濾波去噪。
讓一幅影象減去它的Laplacian運算元可以增強對比度。
void Laplacian(inputArray,outputArray,int ddepth,int ksize=1,double scale=1,double delta=0,int borderType=BORDER_DEFAULT)
*第一個引數,輸入影象,且需為單通道8點陣圖像。
*第二個引數,輸出的邊緣圖。
*第三個引數,輸出影象的影象深度。
*第四個引數,用於計算二階導數的濾波器的孔徑尺寸大小,大小必須為正奇數,預設值為1。
*第五個引數,計算拉普拉斯值的時候可選的比例因子,預設值為1。
*第六個引數,表示在結果存入目標圖之前可選的delta值,預設值為0。
*第七個引數,邊界模式。
對應程式碼
#include<opencv2\opencv.hpp>
#include<opencv2\highgui\highgui.hpp>
using namespace std;
using namespace cv;
//邊緣檢測
int main()
{
Mat img = imread("lol3.jpg");
imshow("原始圖", img);
Mat gray, dst,abs_dst;
//高斯濾波消除噪聲
GaussianBlur(img, img, Size(3, 3), 0, 0, BORDER_DEFAULT);
//轉換為灰度圖
cvtColor(img, gray, COLOR_RGB2GRAY);
//使用Laplace函式
//第三個引數:目標影象深度;第四個引數:濾波器孔徑尺寸;第五個引數:比例因子;第六個引數:表示結果存入目標圖
Laplacian(gray, dst, CV_16S, 3, 1, 0, BORDER_DEFAULT);
//計算絕對值,並將結果轉為8位
convertScaleAbs(dst, abs_dst);
imshow("laplace效果圖", abs_dst);
waitKey(0);
}4 Canny
Canny運算元檢測原理是通過影象訊號函式的極大值來判定影象的邊緣畫素點。邊緣檢測的演算法主演是基於影象強度的一階和二階微分操作,但導數通常對噪聲很敏感,邊緣檢測演算法常常需要根據影象源的資料進行預處理操作,因此必須採用濾波器來改善與噪聲有關的邊緣檢測的效能。在進行Canny運算元邊緣檢測前,應當先對原始資料與高斯模板進行卷積操作,得到的影象與原影象相比有些模糊。通常使用高斯平滑濾波器卷積降噪。
Canny 邊緣檢測運算元,其演算法步驟大體如下:
1) 用高斯濾波器對輸入影象做平滑處理 (大小為 5x5 的高斯核)
2) 計算影象的梯度強度和角度方向 ( x 和 y 方向上的卷積核)
角度方向近似為四個可能值,即 0, 45, 90, 135
3) 對影象的梯度強度進行非極大抑制
可看做邊緣細化:只有候選邊緣點被保留,其餘的點被移除
4) 利用雙閾值檢測和連線邊緣
若候選邊緣點大於上閾值,則被保留;小於下閾值,則被捨棄;處於二者之間,須視其所連線的畫素點,大於上閾值則被保留,反之捨棄
滯後閾值:滯後閾值需要兩個閾值(高閾值和低閾值)
(1)若某一畫素位置的幅值超過高閾值,該畫素被保留為邊緣畫素。
(2)若某一畫素位置的幅值小於低閾值,該畫素被排除。
(3)若某一畫素位置的幅值在兩個閾值之間,該畫素僅僅在連線到一個高於高閾值的畫素時被保留。
void Canny(inputArray,outputArray,double threshold1,double threshold2,int apertureSize=3,bool L2gradient=false)
*第一個引數,輸入影象,且需為單通道8點陣圖像。
*第二個引數,輸出的邊緣圖。
*第三個引數,第一個滯後性閾值。用於邊緣連線。
*第四個引數,第二個滯後性閾值。用於控制強邊緣的初始段,高低閾值比在2:1到3:1之間。
*第五個引數,表明應用sobel運算元的孔徑大小,預設值為3。
*第六個引數,bool型別L2gradient,一個計算影象梯度幅值的標識,預設值false。
#include<opencv2\opencv.hpp>
#include<opencv2\highgui\highgui.hpp>
using namespace std;
using namespace cv;
//邊緣檢測
int main()
{
Mat img = imread("lol3.jpg");
imshow("原始圖", img);
Mat DstPic, edge, grayImage;
//建立與src同類型和同大小的矩陣
DstPic.create(img.size(), img.type());
//將原始圖轉化為灰度圖
cvtColor(img, grayImage, COLOR_BGR2GRAY);
//先使用3*3核心來降噪
blur(grayImage, edge, Size(3, 3));
//執行canny運算元
Canny(edge, edge, 3, 9, 3);
imshow("邊緣提取效果", edge);
waitKey(0);
}5. prewitt
Prewitt運算元是一階邊緣檢測運算元,該運算元對噪聲有抑制作用,不用進行濾波去噪。和Sobel運算元相似,都是在影象空間利用兩個方向模板與影象進行領域卷積來完成的,分別對水平與垂直方向邊緣進行檢測。
Prewitt運算元定位精度不如Sobel運算元,在真正的使用中,一般不會用到這個運算元,效果較差。
6.Marr—Hildreth(LOG)
Marr—Hildreth運算元以高斯函式為平滑運算元,結合拉普拉斯運算元提取二階導數的零交叉理論進行邊緣檢測。效果更好的邊緣檢測器是LoG運算元,它把高斯平滑濾波器和拉普拉斯銳化濾波器結合起來,先平滑掉噪聲,再進行邊緣檢測,所以效果更好。
具體的opencv實現
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <iostream>
using namespace cv;
using namespace std;
void marrEdge(const Mat src, Mat& result, int kerValue, double delta)
{
//計算LoG運算元
Mat kernel;
//半徑
int kerLen = kerValue / 2;
kernel = Mat_<double>(kerValue, kerValue);
//滑窗
for (int i = -kerLen; i <= kerLen; i++)
{
for (int j = -kerLen; j <= kerLen; j++)
{
//生成核因子
kernel.at<double>(i + kerLen, j + kerLen) = exp(-((pow(j, 2) + pow(i, 2)) / (pow(delta, 2) * 2)))
*((pow(j, 2) + pow(i, 2) - 2 * pow(delta, 2)) / (2 * pow(delta, 4)));
}
}
//設定輸入引數
int kerOffset = kerValue / 2;
Mat laplacian = (Mat_<double>(src.rows - kerOffset * 2, src.cols - kerOffset * 2));
result = Mat::zeros(src.rows - kerOffset * 2, src.cols - kerOffset * 2, src.type());
double sumLaplacian;
//遍歷計算卷積影象的拉普拉斯運算元
for (int i = kerOffset; i < src.rows - kerOffset; ++i)
{
for (int j = kerOffset; j < src.cols - kerOffset; ++j)
{
sumLaplacian = 0;
for (int k = -kerOffset; k <= kerOffset; ++k)
{
for (int m = -kerOffset; m <= kerOffset; ++m)
{
//計算影象卷積
sumLaplacian += src.at<uchar>(i + k, j + m)*kernel.at<double>(kerOffset + k, kerOffset + m);
}
}
//生成拉普拉斯結果
laplacian.at<double>(i - kerOffset, j - kerOffset) = sumLaplacian;
}
}
for (int y = 1; y < result.rows - 1; ++y)
{
for (int x = 1; x < result.cols-1; ++x)
{
result.at<uchar>(y, x) = 0;
//領域判定
if (laplacian.at<double>(y - 1, x)*laplacian.at<double>(y + 1, x) < 0)
{
result.at<uchar>(y, x) = 255;
}
if (laplacian.at<double>(y, x - 1)*laplacian.at<double>(y, x + 1) < 0)
{
result.at<uchar>(y, x) = 255;
}
if (laplacian.at<double>(y + 1, x - 1)*laplacian.at<double>(y - 1, x + 1) < 0)
{
result.at<uchar>(y, x) = 255;
}
if (laplacian.at<double>(y - 1, x - 1)*laplacian.at<double>(y + 1, x + 1) < 0)
{
result.at<uchar>(y, x) = 255;
}
}
}
}
int main()
{
Mat srcImage = imread("D:\\3.jpg");
if (!srcImage.data)
return -1;
Mat edge,srcGray;
cvtColor(srcImage, srcGray, CV_RGB2GRAY);
marrEdge(srcGray, edge, 9, 1.6);
imshow("srcImage", srcImage);
imshow("edge", edge);
waitKey(0);
return 0;
}