第4章第1節練習題4 二叉樹高度和寬度統計
為了方便說明二叉樹的遞迴傳值過程,這裡首先給出一個基本的二叉樹結構。
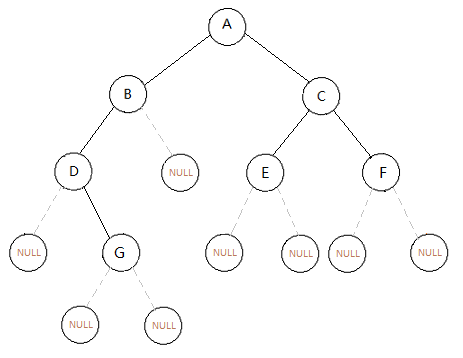
圖中值為NULL的節點實際是不存在的,故與父親節點之間的連線用灰色的虛線表示。只是為了便於說明,才假設了一個NULL的空節點。
以下圖中,黃色的線表明了傳值的方向;綠色的數值表明了子節點傳到父親節點時的值,即根據遞迴公式計算便可。
一.計算二叉樹的高度(遞迴/非遞迴)
遞迴方式實現
對於高度的計算,首先是從葉子結點算起,假設葉子結點下面的NULL節點高度為0,則葉子結點的高度便為1,那麼葉子結點的雙親節點便為2,以此類推便可以得到根節點的高度,這樣也就得到了整棵二叉樹的高度。其基本的遞迴公式如下:
具體執行過程可以參考下圖,
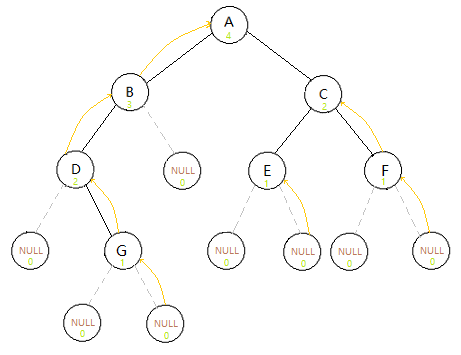
當指標遍歷到葉子結點的孩子結點(NULL結點)時,向葉子結點返回0,然後由葉子結點判斷來自左邊的孩子結點(NULL結點)和來自右邊的孩子結點(其實還是NULL結點)的返回值誰比較大,因為葉子結點處的值均由NULL結點返回,因此相等,則取右邊NULL結點的值,然後+1,表示葉子結點的高度。然後再由葉子結點向其雙親節點返回值,依次類推便可以得到整棵樹的高度。
演算法描述如下
int 非遞迴方式實現
採用層次遍歷的演算法,設定變數cnt表示當前結點所在層次,設定變數last指向當前層最右結點,每次層次遍歷出隊時與last相比較,如果兩者相等,那麼層數+1,並讓last指向下一層最右結點,直至遍歷完成。level的值即為二叉樹的高度。
關於last指標的特性應該注意到,當隊首指標front指向last識別符號時,其隊尾指標rear剛好會指向下一層的隊尾元素。
演算法描述如下
int CntHeight_norecursive(BiTNode* T){
BiTNode* p=T;
SqQueue Q;
InitQueue(&Q);
EnQueue(&Q,p);
int cnt=0;
int last=1;
while(IsEmptyQueue(&Q)!=0){
p=DeQueue(&Q);
if(p->lchild!=NULL){
EnQueue(&Q,p->lchild);
}
if(p->rchild!=NULL){
EnQueue(&Q,p->rchild);
}
if(Q.front==last){
cnt++;
last=Q.rear;
}
}
return cnt;
}二.計算二叉樹的寬度(非遞迴)
關於遞迴方式,個人沒有想到特別好的解決方案,這裡主要以非遞迴方式實現。
非遞迴方式的實現方式與計算二叉樹寬度的非遞迴實現方式類似,完全可以利用last指標的特性,即當隊首指標front指向last時,此時隊尾指標rear會剛好指向二叉樹下一層的最右邊結點,此時只需要用隊尾指標rear減去隊首指標便可以得到該層的寬度。而二叉樹的寬度則指的是從根節點到葉子結點的某層中元素最多的一層,因此只需要將每層的寬度儲存下來取最大值便可。
非遞迴方式實現
int CntWidth_norecursive(BiTNode* T){
BiTNode* p=T;
SqQueue Q;
InitQueue(&Q);
EnQueue(&Q,p);
int cnt=0;
int last=1;
int level[MaxSize]={0};
while(IsEmptyQueue(&Q)!=0){
p=DeQueue(&Q);
if(p->lchild!=NULL){
EnQueue(&Q,p->lchild);
}
if(p->rchild!=NULL){
EnQueue(&Q,p->rchild);
}
if(Q.front==last){
level[cnt++]=Q.rear-Q.front;
last=Q.rear;
}
}
int max=level[0];
for(int i=0;i<cnt;i++){
if(max<level[i]){
max=level[i];
}
}
return max;
}具體程式碼見附件。
附件
//統計二叉樹的高度和寬度
//AB#DG###CE##F##
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 10
typedef char ElemType;
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
typedef struct{
BiTNode* data[MaxSize];
int front, rear;
}SqQueue;
BiTNode* CreateBiTree(BiTNode*);
void InitQueue(SqQueue*);
void EnQueue(SqQueue*,BiTNode*);
BiTNode* DeQueue(SqQueue*);
int IsEmptyQueue(SqQueue*);
void PreOrder(BiTNode*);
void InOrder(BiTNode*);
int CntHeight_recursive(BiTNode*);
int CntHeight_norecursive(BiTNode*);
int CntWidth_norecursive(BiTNode*);
//-------------------------------------------------------------------------------------
int main(int argc, char* argv[]){
BiTNode* T=(BiTNode*)malloc(sizeof(BiTNode));
T=CreateBiTree(T);
PreOrder(T);printf("\n");
InOrder(T);printf("\n");
int count;
count=CntHeight_recursive(T);
printf("recursive:The height of BiTree is %d\n",count);
count=CntHeight_norecursive(T);
printf("non-recursive:The height of BiTree is %d\n",count);
count=CntWidth_norecursive(T);
printf("non-recursive:The Width of BiTree is %d\n",count);
return 0;
}
//-------------------------------------------------------------------------------------
BiTNode* CreateBiTree(BiTNode* T){
ElemType ch;
scanf("%c",&ch);
if(ch=='#'){
return NULL;
}
T=(BiTNode*)malloc(sizeof(BiTNode));
T->data=ch;
T->lchild=CreateBiTree(T->lchild);
T->rchild=CreateBiTree(T->rchild);
return T;
}
//-------------------------------------------------------------------------------------
//統計二叉樹的高度(遞迴)
int CntHeight_recursive(BiTNode* T){
int lh,rh;
if(T==NULL){
return 0;
}
lh=CntHeight_recursive(T->lchild);
rh=CntHeight_recursive(T->rchild);
return lh>rh?lh+1:rh+1;
}
//統計二叉樹的高度(非遞迴)
int CntHeight_norecursive(BiTNode* T){
BiTNode* p=T;
SqQueue Q;
InitQueue(&Q);
EnQueue(&Q,p);
int cnt=0;
int last=1;
while(IsEmptyQueue(&Q)!=0){
p=DeQueue(&Q);
if(p->lchild!=NULL){
EnQueue(&Q,p->lchild);
}
if(p->rchild!=NULL){
EnQueue(&Q,p->rchild);
}
if(Q.front==last){
cnt++;
last=Q.rear;
}
}
return cnt;
}
//-------------------------------------------------------------------------------------
//統計二叉樹的寬度(非遞迴)
int CntWidth_norecursive(BiTNode* T){
BiTNode* p=T;
SqQueue Q;
InitQueue(&Q);
EnQueue(&Q,p);
int cnt=0;
int last=1;
int level[MaxSize]={0};
while(IsEmptyQueue(&Q)!=0){
p=DeQueue(&Q);
if(p->lchild!=NULL){
EnQueue(&Q,p->lchild);
}
if(p->rchild!=NULL){
EnQueue(&Q,p->rchild);
}
if(Q.front==last){
level[cnt++]=Q.rear-Q.front;
last=Q.rear;
}
}
int max=level[0];
for(int i=0;i<cnt;i++){
if(max<level[i]){
max=level[i];
}
}
return max;
}
//-------------------------------------------------------------------------------------
//先序遍歷
void PreOrder(BiTNode* T){
if(T==NULL){
return;
}
printf("%c",T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
//中序遍歷
void InOrder(BiTNode* T){
if(T==NULL){
return;
}
InOrder(T->lchild);
printf("%c",T->data);
InOrder(T->rchild);
}
//-------------------------------------------------------------------------------------
void InitQueue(SqQueue* Q){
Q->front=0;
Q->rear=0;
}
void EnQueue(SqQueue* Q, BiTNode* T){
if((Q->rear+1)%MaxSize==Q->front){
return;
}
Q->data[Q->rear++]=T;
}
BiTNode* DeQueue(SqQueue* Q){
if(Q->front==Q->rear){
return NULL;
}
return Q->data[Q->front++];
}
int IsEmptyQueue(SqQueue* Q){
if(Q->rear==Q->front){
return 0;
}else{
return -1;
}
}