問題描述

回型矩陣即使用二維陣列完成來繞圈圈似的賦值，舉例說明如下所示的形式即為回型陣列。

演算法思想

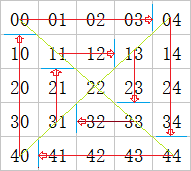
就單純的在二維陣列中按照某種順序輸出連續的數字而言，實際上是玩弄陣列下標遊戲。因此將回型陣列寫成下標所表示的形式，如下圖所示，其中00的意思是陣列下標(0,0)，後面的以此類推。

當得到上述所示的下標所列出來的圖形時，可以發現回型陣列主要由的一個輪迴剛好是矩陣的四條邊，而第一圈的最後一條豎直的邊並不與第一圈的開始重合，因此為了方便處理，可以將每條邊的“最後一個元素”單獨處理，然後畫出其主對角線和副對角線，可以得到下圖，其中綠色的兩條斜線分別為主對角線和副對角線。

從圖中可以看到：

• 數字從1~4的過程中，陣列下標從00~03；即行下標保持不變，而列下標保持遞增；
• 數字從5~8的過程中，陣列下標從04~34；即行下標保持遞增，而列下標保持不變；
• 數字從9~12的過程中，陣列下標從44~41；即行下標保持不變，而列下標保持遞減；
• 數字從13~16的過程中，陣列下標從40~10；即行下標保持遞減，而列下標保持不變；

上述過程完成了一個輪迴，其他的與上面的步驟相似。對上述步驟分析結合上圖，可以得到
水平方向：開始於主對角線，結束於副對角線；
豎直方向：開始於副對角線，結束於主對角線；

對於主對角線上的元素下標滿足行下標等於列下標

對於副對角線上的元素行下標與列下標之和等於定常數，而這個定常數恰好為矩陣的維數減1

由此可以得到主對角線元素下標為：(i,i);
副對角線下標為：(i,N-1-i)或(N-1-i,i);

那麼再分析下上述的輪迴，便可以得到通項表示式：

• 數字從1~4的過程中，陣列下標從(i,i)->(i,N-2-i);
• 數字從5~8的過程中，陣列下標從(i,N-1-i)->(i-1,i);
• 數字從9~12的過程中，陣列下標從(i,i)->(i，N-2-i);
• 數字從13~16的過程中，陣列下標從(N-1-i,i)->(i-1,i);
  注：上述的i
  只是一種表示方式，不同行列數字變化的過程中，i並不相同。

這裡應該注意到該矩陣的維數是奇數還是偶數。如果是奇數，應該注意到最裡面的那個數是需要開啟新的一輪輪迴的，故應特殊對待；而對於偶數，最後一次輪迴就可以完成所有的賦值過程。
。
綜上所述，演算法的描述如下。

演算法描述

void ClipArray(int A[][N]){
    int cnt=0;
    for(int i=0;i<N/2;i++){
        //從左向右
        for(int j=i;j<N-1-i;j++){
            A[i][j]=++cnt;
        }
        //從上向下
        for(int j=i;j<N-1-i;j++){
            A[j][N-1-i]=++cnt;
        }
        //從右向左
        for(int j=N-1-i;j>i;j--){
            A[N-1-i][j]=++cnt;
        }
        //從下向上
        for(int j=N-1-i;j>i;j--){
            A[j][i]=++cnt;
        }
    }
    if(N%2!=0){
        A[N/2][N/2]=++cnt;
    }
}

具體程式碼見附件。

附件

#include<stdio.h>
#define N 4

void ClipArray(int (*)[N]);
void Show(int (*)[N]);

int main(int argc,char* argv[]){
    int Arry[N][N]={{0}};
    ClipArray(Arry);
    Show(Arry);
    return 0;
}

void ClipArray(int A[][N]){
    int cnt=0;
    for(int i=0;i<N/2;i++){
        //從左向右
        for(int j=i;j<N-1-i;j++){
            A[i][j]=++cnt;
        }
        //從上向下
        for(int j=i;j<N-1-i;j++){
            A[j][N-1-i]=++cnt;
        }
        //從右向左
        for(int j=N-1-i;j>i;j--){
            A[N-1-i][j]=++cnt;
        }
        //從下向上
        for(int j=N-1-i;j>i;j--){
            A[j][i]=++cnt;
        }
    }
    if(N%2!=0){
        A[N/2][N/2]=++cnt;
    }
}

void Show(int A[][N]){
    for(int i=0;i<N;i++){
        for(int j=0;j<N;j++){
            printf("%3d",A[i][j]);
            if(j==N-1){
                printf("\n");
            }
        }
    }
}