Matlab實現簡單K-means聚類演算法
K-means演算法簡要思想:
演算法接受引數 k ;然後將事先輸入的n個數據物件劃分為 k個聚類以便使得所獲得的聚類滿足:同一聚類中的物件相似度較高;而不同聚類中的物件相似度較小。
(1)適當選擇k個類的初始中心;
(2)在第k次迭代中,對任意一個樣本,求其到各中心的距離,將該樣本歸到距離最短的中心所在的類;
(3)利用均值等方法更新類的中心值;
(4)對於所有的c個聚類中心,如果利用(2)(3)的迭代法更新後,中心值保持不變或者滿足變化距離小於一個精度或者達到最大迭代次數,則迭代結束,否則繼續迭代。
實現步驟:
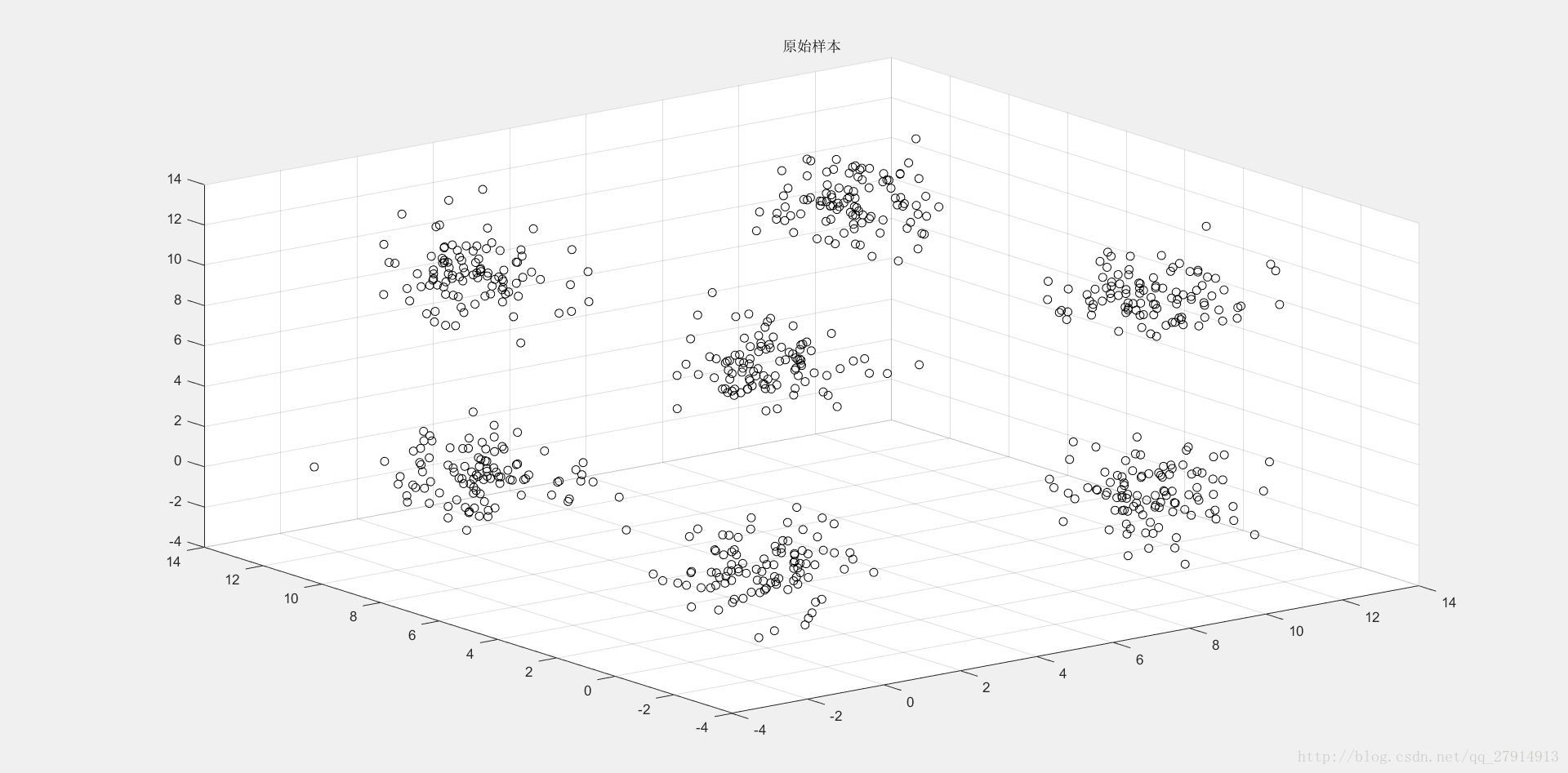
實驗提供了兩組資料(二維和三維),演算法都能適用,這裡我們以三維資料作為說明。首先讀入資料,用scatter3將三維資料通過散點圖顯示出來:
load 3d-data.mat; %load資料,存在變數r中
figure(1);scatter3(r(:,1),r(:,2),r(:,3),'k');title('原始樣本');結果見下圖1:
圖1 三維樣本集原始資料散點圖
通過圖1可以明顯看出,樣本集聚為7個簇,因此可將K初始化為7,然後隨機選取7箇中心點,存於clusters矩陣中:
clusters=zeros(K,cols);
for i=1:K
clusters(i,:)=r(floor(rand*rows),:); %隨機選取K個質心 質心選取後,需要計算每個樣本點與K個質心的距離,存於dist矩陣中,並從此處開始迭代(for i=1:maxiter):
dist=zeros(rows,K);
for iter=1:maxiter
for i=1:rows
for j=1:K
dist(i,j)=sqrt(sum(( r(i,:)-clusters(j,:)).^2)); %dist存的是每一個樣本資料與K個質心的距離,大小為rows*K
end
end矩陣dist中存了每個樣本集與K個質心的距離,維數為rows*K,由於我們需要選出距離最小的那個質心,也就是要從矩陣dist每一行中選出最小數所在的位置,我們可以先將dist中每一行升序排序,最小的那個數就在每一行的首列,然後與原來dist一行數進行比較,找出最小距離的位置,即可分類:
distsort=sort(dist,2); %對dist中每一行資料進行升序排序
label=zeros(rows,1);
for i=1:rows
for j=1:K
if(distsort(i,1)==dist(i,j))
label(i,1)=j; %每個樣本所屬的類別
end
end
end類別存於矩陣label中,維數為rows*1。接下來,需要對每一類中的所有樣本點進行求平均,具體操作是將所有同類樣本點相加後除於個數,新質心存於new_clusters矩陣中:
sum_sample=zeros(K,cols); %每個簇的樣本相加和
num_sample=zeros(K,1); %每個簇的樣本個數
for i=1:K
for j=1:rows
if(label(j,1)==i)
sum_sample(i,:)=sum_sample(i,:)+r(j,:);
num_sample(i,1)=num_sample(i,1)+1;
end
end
end
new_clusters=zeros(K,cols);
for i=1:K
new_clusters(i,:)=sum_sample(i,:)/num_sample(i,1); %每個簇的所有樣本相加求平均作為新質心
end當前後兩次質心之間的距離變化小於一個設定精度時,判定此時達到收斂。由於要保證所有質心距離變化都小於某個精度,因此需要計算質心變化距離並判斷變化不大的質心個數是否為K(即全部k個質心都不發生明顯變化):
PRECISION=0.001; %精度
clu_dist=zeros(K,1);
for i=1:K
clu_dist(i,1)=sqrt(sum((new_clusters(i,:)-clusters(i,:)).^2)); %求前後兩次質心距離
end
count=0; %質心不發生明顯變化的質心個數
for i=1:K
if(clu_dist(i,1)<PRECISION)
count=count+1;
end
end當全部K個質心都不發生明顯變化時,列印輸出此時迭代了多少次,並將聚類後的散點圖畫出,由於要用不同顏色標出,而且畫散點圖是一個一個畫,因此需要多個判斷語句:
if(count==K) %K個質心都不發生明顯變化
fprintf('收斂於第 %d 次迭代\n',iter); %輸出 第幾次達到收斂
figure(2);
for i=1:rows
if(label(i,1)==1)
scatter3(r(i,1),r(i,2),r(i,3),'b');hold on; %藍色
else if(label(i,1)==2)
scatter3(r(i,1),r(i,2),r(i,3),'g');hold on; %綠色
else if(label(i,1)==3)
scatter3(r(i,1),r(i,2),r(i,3),'r');hold on; %紅色
else if(label(i,1)==4)
scatter3(r(i,1),r(i,2),r(i,3),'k');hold on; %黑色
else if(label(i,1)==5)
scatter3(r(i,1),r(i,2),r(i,3),'c');hold on; %青色
else if(label(i,1)==6)
scatter3(r(i,1),r(i,2),r(i,3),'y');hold on; %黃色
else if(label(i,1)==7)
scatter3(r(i,1),r(i,2),r(i,3),'m');hold on; %粉紅
end
end
end
end
end
end
end
end
title('k-means聚類後');
break; %跳出迭代
else clusters=new_clusters; %否則繼續迭代
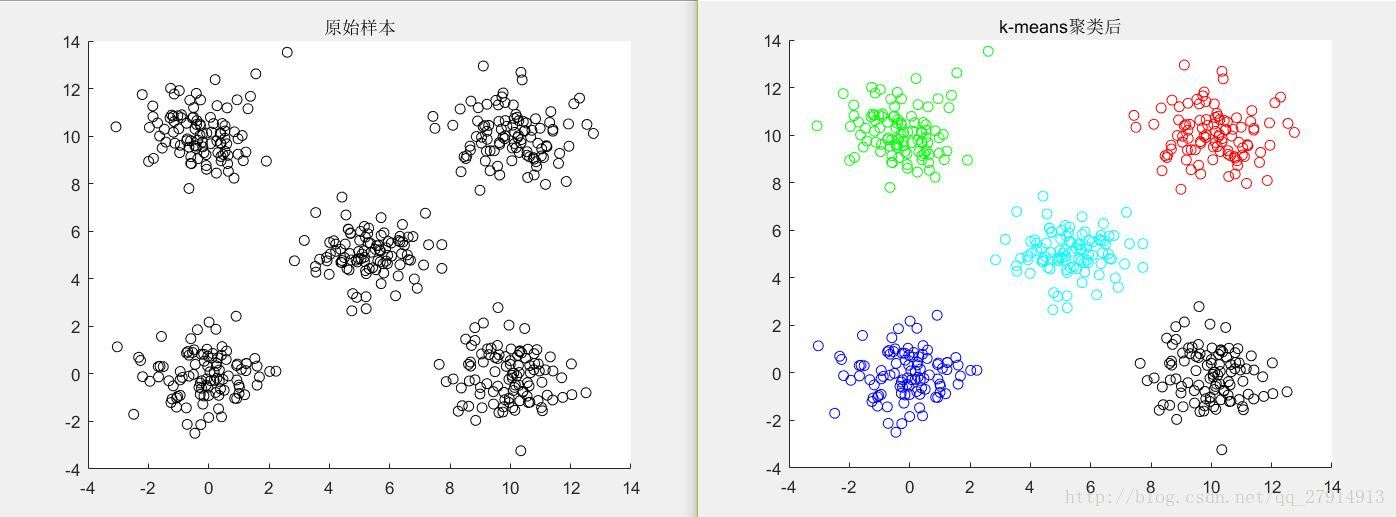
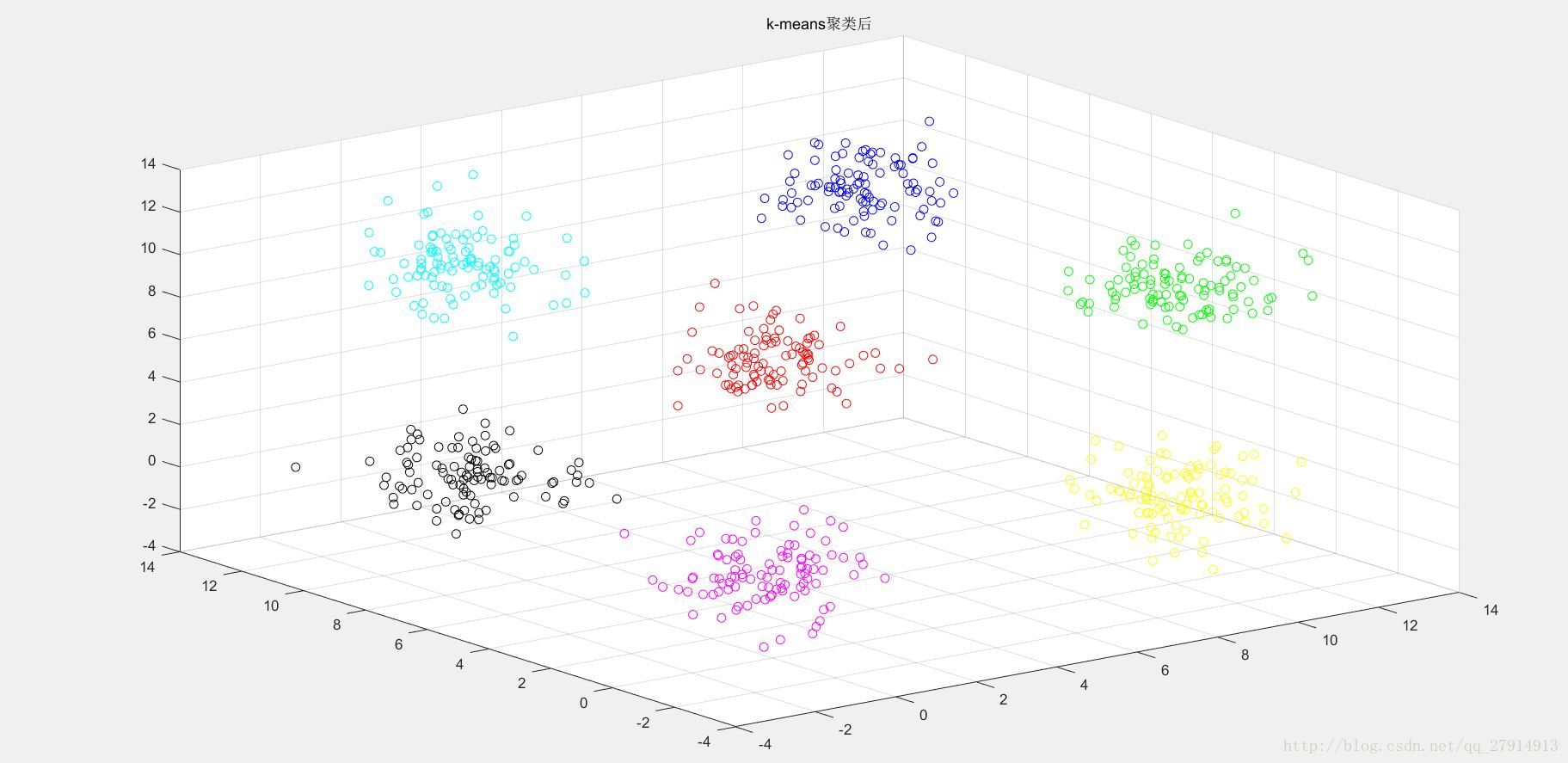
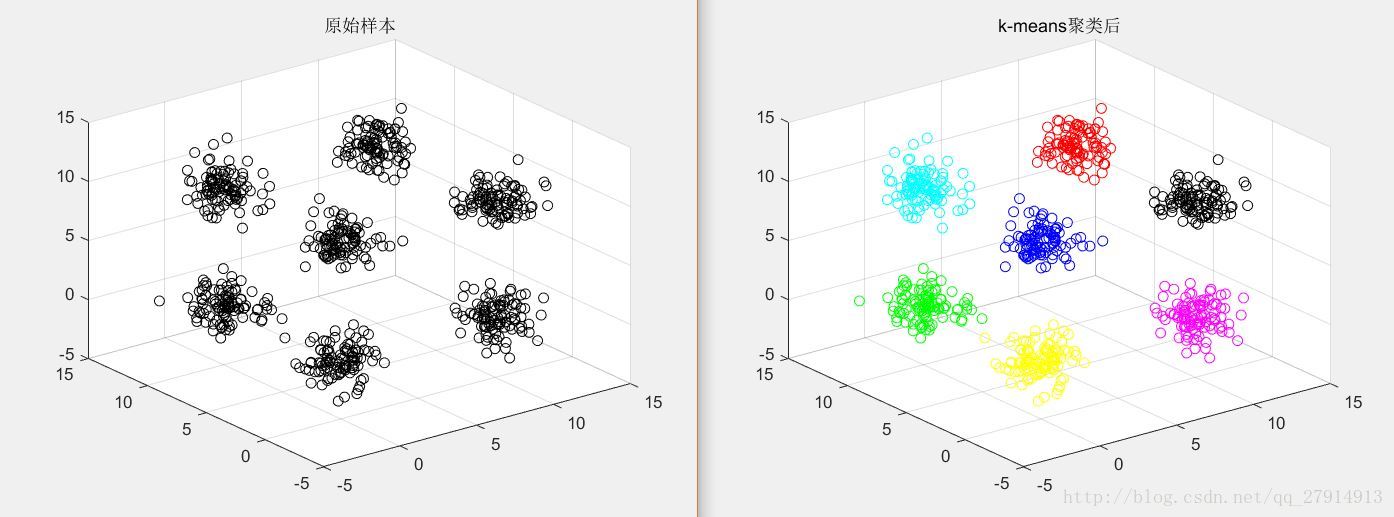
end收斂後,輸出聚類後的樣本點並跳出迭代,否則將此時的質心作為新質心繼續迭代。至此,演算法結束。圖2是二維資料演算法結果,圖3-圖6是三維資料點聚類後結果:
圖2 二維資料聚類前後對比
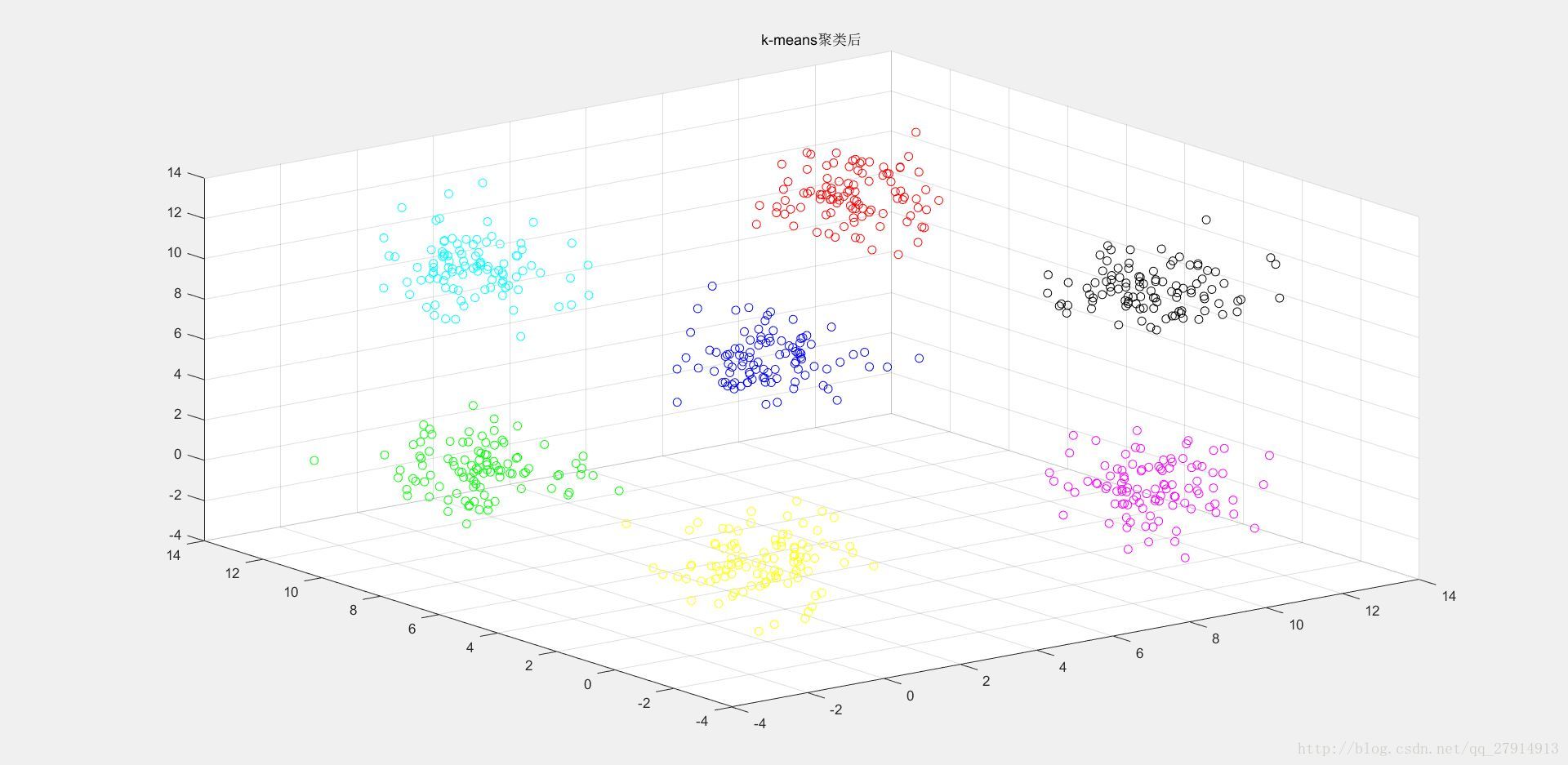
圖3 三維資料聚類後

圖4 三維資料聚類後
圖5 三維資料聚類後
圖6 三維資料聚類前後對比
分析:
由圖3-6可看出,該演算法得出的結果並不穩定,原因就是該演算法對初始質心選取很敏感,隨機選取質心可能會得到錯誤結果並且迭代次數也會變大,若初始質心剛好分別處於7個簇之中,那麼演算法結果就會穩定了。初始質心的距離不應太近,因此可做以下優化:
a) 從輸入的資料點集合中隨機選擇一個點作為第一個聚類中心
b) 對於資料集中的每一個點,計算它與已選擇的聚類中心中最近聚類中心的距離D(x) c) 選擇一個新的資料點作為新的聚類中心,選擇的原則是D(x)較大的點,
被選取作為聚類中心的概率較大
d) 重複b和c直到選擇出k個聚類質心
e) 利用這k個質心來作為初始化質心去執行標準的K-Means演算法
這是對初始質心選取的優化,還有一些距離計算的優化等,都是對K-means的改進。
總結:
K-means是個簡單實用的演算法,原理簡單,實現容易,收斂速度快,結果較優;缺點是K值的選取不好把握,初始質心不好選取,對不是凸的資料集比較難收斂,迭代得到的結果只是區域性最優,並且對噪聲點敏感。