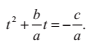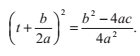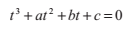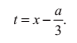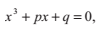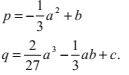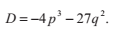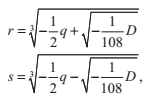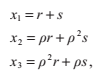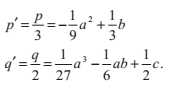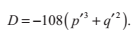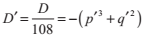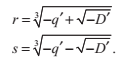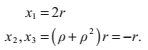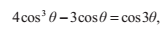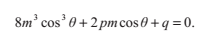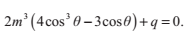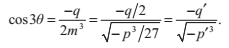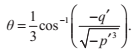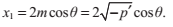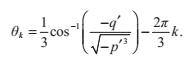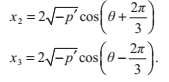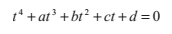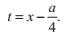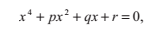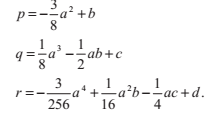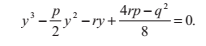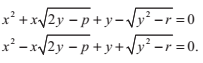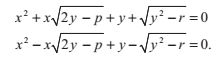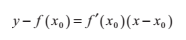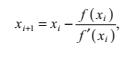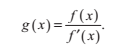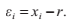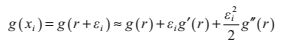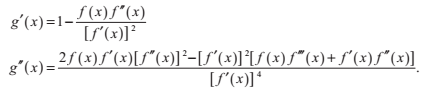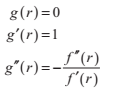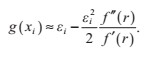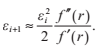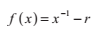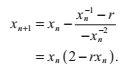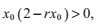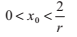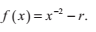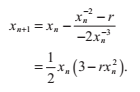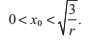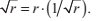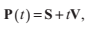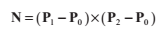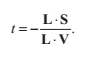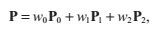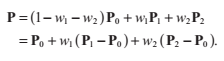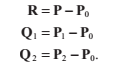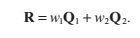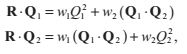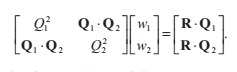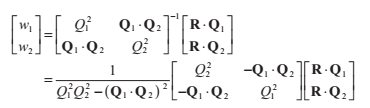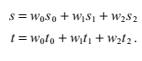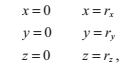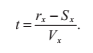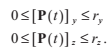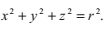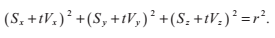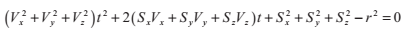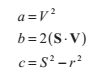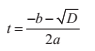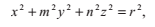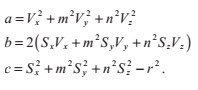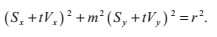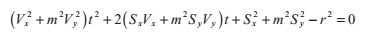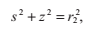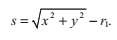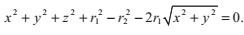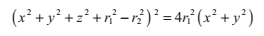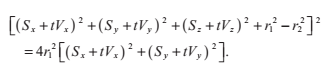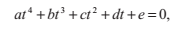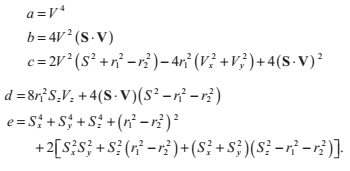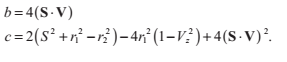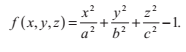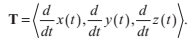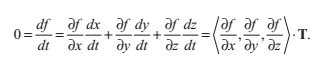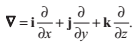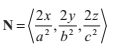[圖形學] 光線追蹤中的數學方法
reference: 《Mathematics for 3D Game Programming and Computer Graphics》
目錄
| 6.1 求根 6.1.1 二次多項式 6.1.2 三次多項式 6.1.3 四次多項式 6.1.4 牛頓法 6.1.5 倒數及平方根的優化 6.2 表面相交 6.2.1 光線與三角形的相交 6.2.2 光線與立方體的相交 6.2.3 光線與球體的相交 6.2.4 光線與圓柱體的相交 6.2.5 光線與圓環體的相交 6.3 法線計算 6.4 反射和折線向量 6.4.1 反射向量計算 6.4.2 折射向量計算 |
光線追蹤這一術語是指跟隨光束來決定它們和世界中的哪個物體相交的演算法。
它的應用包括光照紋理的生成、判斷可見性、碰撞檢測,以及視線檢測。這一章描述了當光線與物體相交時如何找到它們的交點,以及當光線與反射或者折射表面相交時,如何改變光線的路徑。
1.求根
為了找到方程為P(t) = S + tV的直線與表面相交的交點,我們需要求得關於t的n次多項式的根。對於平面而言,這個多項式的次數是1,它的解很好求。對於二次曲面,例如球面或者圓柱面,多項式的次數是2,我們可以求解二次方程來找到一個解。而對於更加複雜的曲面,例如樣條曲面和圓環面,多項式的次數達到了3或4,在這種情況下,我們仍然可以分析找到解,但是這將花費更多的計算代價。二次,三次以及四次多項式的解析解將在這個部分中介紹。不過,三次以及四次方程解的完整推導已經超越了這本書的範圍。我們同樣也會驗證一個數值求根技術:牛頓迭代法。
1.1 二次多項式
我們可以使用一些代數運算來求的t的二次多項式的根。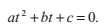
兩邊同時減去c,並且同除a:
通過同時加上b^2/(4*a^2),我們可以得到左式的一個完全平方
把左式寫成平方的形式,並把右式通分
開方並同減b/(2*a)
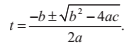
這就是著名的二次求根公式。D = b^2 - 4*a*c這個量被稱為多項式的判別式,它反映了這個多項式有多少個實根。
如果D>0,那麼它有兩個實根,如果D=0,那麼它有一個實根,它的值為t=-b/(2*a)。剩下的一種情況是D<0,這時候它沒有實根。
計算判別式可以讓我們在不求出具體解的情況下,判斷光線是否與物體相交。
1.2 三次多項式
形式為
的三次多項式(我們使用了一些必要的除法來保證首項係數為1)可以通過如下的引數替換,轉換為一個沒有二次係數的式子。
轉換後我們得到:
其中:
三次方程的判別式為
我們設:
現在我們可以這樣表達等式的三個複數根:
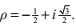 (注意
(注意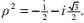 )
)我們可以使用換元來極大地簡化我們的式子
設
我們現在可以這樣表達r和s:
和二次方程一樣,判別式告訴了我們實根的存在性。如果D‘<0, 方程給出的x1的值表示的是方程的唯一實根。
如果D‘ = 0,我們有r = s,所以現在存在兩個實數根,包括一個雙重根:
剩下一種情況D‘>0中,方程有三個不同的根。不幸的是,我們仍然需要利用複數來計算這些解。此外還有另一種不需要複數運算的方法,這個方法主要依賴於以下這個三角等式:
我們可以用尤拉公式來證明這一方程的正確性。對於
我們做一個換元
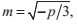
(注意:為了保證D‘為正,p必須為負)用-3m^2代替p,並把公因數2m^3拿到外面:
代入前面提到的三角等式,並且計算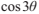
由於D‘>0,根據
推斷出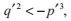
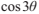
所以,我們可以得到原方程(引數為x)的一個解:
由於對任意整數k,都有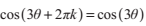
通過選擇k餘3的三個不同的值0,1,2,可以得到不同的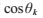
1.3 四次多項式
一個四個多項式有如下的形式:
(同樣地,我們做一些必要的除法來保證首項係數為1)可以通過換元轉換為沒有三次項的式子:
這將原式轉換為:
其中:
一旦我們找到了方程的一個解x,我們減去a/4,就能得到原式的解t。
要求出四次方程的根,首先要解出以下三次方程的根:
令y為這個方程的任一實數根。如果q>=0,那麼四次方程的解等價於這兩個二次方程的解:
如果q<0,那麼四次方程的解等價於這兩個二次方程的解:
1.4 牛頓迭代法
牛頓迭代法,通常簡稱為牛頓法,是一種通過迭代一個與函式及其導數相關的式子,找到任意連續函式的根的數值分析技術。
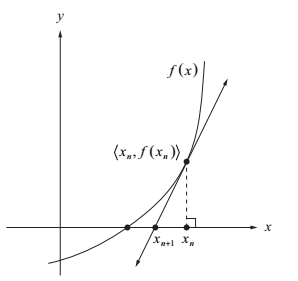
(函式的切線與x軸的交點逼近函式的根)
假設我們想要找到上圖中函式f的根。現在,讓我們假設我們有一個關於函式根的最初猜測值x0(主要關注的是如何快速選擇合適的值)。過點(x0,f(x0))的切線的斜率是由導數f'(x0)來刻畫的。我們可以把這條切線用下面的式子來表示:
注意到,這條切線與x軸的交點相比起我們初始的猜測值x0更接近與真實的解。當y = 0的時候,我們可以得到x的迭代式:
在這裡,我們用xi來代替x0, 用xi+1來代替x。我們反覆代入這個式子,計算得到一個序列x0,x1,x2……,它們的值在正確條件下將不斷逼近 f 的根。
牛頓法能相當快地收斂於根,因而達到一定精確度時需要的迭代次數非常少。我們事實上可以顯示出牛頓法是二次收斂的,這就意味著每一次迭代後,近似根的有效數字個數成倍增長。為了證明這一點,我們設:
令r為函式 f 實際的根,我們定義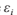
我們把這個式子代入x的迭代式,得到:
我們可以用泰勒公式的前三項來近似估計g(xi)的值:
g(x)的一次二次導數可以寫為:
由於f(r) = 0,當x = r時,這個表示式可以極大的簡化,這時函式g以及它的一次二次導數為:
我們把這些帶入到前面的泰勒展開式,得到:
最終,我們把這個代入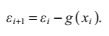
牛頓法並不保證收斂到解。特別地,如果初始的猜想選擇了某一點,使得函式的導數為0,那麼切線將是水平的,不會和x軸相交,我們無法進行執行下去。初始的猜想必須在某種程度上接近實際解來保證收斂。當我們尋找一條線與複雜物體的交點時,我們通常能夠通過求這條線與物體的簡單包圍體的交點,來找到一個好的初始點。例如,如果我們想要找到P(t) = S + tV這條光線與圓環的交點,我們首先可以求這條光線與包圍著圓環的立方包圍盒的交點,然後再利用這個值作為我們求與圓環交點的初始猜想值。
1.5 倒數和平方根的優化
絕大多數的現代CPU,包括絕大多數的圖形硬體,都可以近似一個數的倒數以及倒數平方根到一定的精確度。硬體提供的計算結果可以利用牛頓法得到更高的精確度。
數字r的倒數可以通過求以下這個函式的根得到:
因為f(1/r) = 0。將這個式子代入前面的迭代式,我們得到:
這個式子可以被反覆迭代以得到數字r的高精度倒數,如果每個xi都大於0的話。這取決於這樣一個事實:函式f(x)在x = 0時會達到一個奇點。把這個條件施加到x1上,我們可以確定初始的x0一定會處在的區間是什麼。因為x1一定大於0,我們就能得到:
這樣就計算出了x0的取值範圍:
因此,初始的近似不會比2/r更差。
r的平方根的倒數可以通過計算如下這個方程的根得到:
同樣代入迭代式,我們得到:
只要每個xi>0,這個序列都是收斂的,所以我們的初始解必然滿足:
一旦我們計算出了可接受精度的倒數平方根,r的平方根能通過單一的乘法計算得到,因為
2.表面相交
計算一條光線與一個面的交點是光線追蹤的核心。
我們這樣定義光線:
其中S代表光線的起始位置,V代表光線指向的方向。在這一章節中,我們使用常見的物體來講述光線相交的特定解(其餘的物體留作練習)。除了三角形外,相交都是在物體空間計算的,在這個空間裡物體的中心和座標原點重合,它的軸線沿著座標軸線展開。要完成與任意朝向的物體相交的計算,首先要把光線轉換到物體空間。一旦檢測到了相交,相關的資訊如交點以及該點的法線向量又被轉換回世界空間。
2.1 光線與三角形的相交
一個三角形面片由它三個頂點P0,P1,P2的位置來描述。我們可以通過計算以下法線來確定這個三角形所在的平面:
到原點有符號的距離d,是由向量N與平面任意點的點乘的相反數計算得到的。所以我們選擇頂點P0來構建一個4D平面向量L={N,-N . P0}。正如我們在前面的章節提到的,光線與面L交點關聯的t的值為:
如果L.V = 0,那麼就不會相交。否則,我們將t反代到光線方程中,得到光線與三角形平面的交點P。
我們現在面臨著這樣一個問題,我們需要判斷這個點P是否在三角形邊的內部。我們通過計算P關於三角形頂點p1,p2,p3的質心座標來判斷。質心座標表達了三角形頂點的權值平均數,它們用w0,w1,w1來表示:
其中w0+w1+w2 = 1.我們用1-w1-w2來替代w0,得到以下式子
我們定義與p0相關的式子:
把原來的表示式簡化為:
等式兩邊同時進行點乘,首先是和Q1,然後再是Q2,我們得到這樣兩個式子:
如果把它們寫成矩陣形式,是這樣的:
我們可以按如下方式輕鬆地求出w1和w2:
點R在三角形內部當且僅當三個權值w1,w2,w3都是非負的。由於w0 = 1- w1 - w2,這就意味著w1 + w2 <=1.
如果頂點p0,p1,p2有任何相關的屬性,如顏色或者座標集合,那麼我們都可以利用w0,w1,w2通過插值計算得到點R的這一屬性。例如,如果P0,P1,P2的紋理座標分別為<s0,t0>,<s1,t1>和<s2,t2>,那麼R點的紋理座標<s,t>可以表達為:
2.2 光線與立方體的相交
一個立方盒是由以下六個平面方程描述的:
其中,rx,ry和rz表達了這個盒子所處的範圍。在計算光線的交點時,我們最多需要考慮三個這樣的平面,因為至少有三個平面是背對光線的朝向V的。我們可以逐個檢查V的每個分量來決定我們要計算哪些平面。例如,如果Vx = 0,那麼我們就知道這條光線無法與平面x=0以及平面x=rx相交,因為V和它們是平行的。如果Vx > 0,那麼我們不需要檢測和平面x=rx的相交,因為它相對於光線視角來說,是處在背面的。類似的,如果Vx<0,我們不需要檢測和平面x=0的相交。同樣的規則也適用於V的y和z分量。
我們一旦找到了光線與平面的交點,就必須通過檢查和平面平行的兩個方向對應的座標,來檢查這個點是否落在立方盒的面上。例如,t的值對應著光線與平面x=rx的交點:
為了保證落在盒子的相應面內,點P(t)的y和z座標需要滿足:
如果任一條件不成立,那麼就不存在和這個面的交點。如果兩個條件都成立,那麼就一定能找到一個相交,這時候,我們就不需要測試其它任何平面了,因為不會再發生比這個更好的相交了。(no closer intersection can occur)
2.3 光線與球體的相交
一個與球心在原點,半徑為r的球體可以由以下方程表示:
我們用光線P(t)的方程來代替x,y,z,得到:
展開平方,並且以t為主元合併同類項,得到以下方程:
我們可以用以向量S,V表示的a,b,c來表達方程的係數:
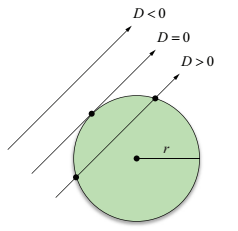
計算判別式D = b^2 - 4ac 能夠告訴我們光線是否與球體相交。正如下圖所顯示的,如果D<0, 那麼不會發生相交;如果D = 0,那麼光線與球體相切;如果D > 0,那麼存在兩個不同的交點。如果光線和球體有兩個交點,那麼離光線原點S 更接近的交點(對應著t值中更小的那一個),通常寫作:
因為我們可以保證a是正數。
光線與橢球體的相交可以把原來的球體方程替換成以下這個方程來計算:
其中m是x半軸長度與y半軸長度的比例係數,n是x半軸長度與z半軸長度的比例係數。我們把光線方程的分量代入這個方程,可以得到另一個二次多項式,它的係數為:
類似的,我們用判別式來判斷相交是否發生。如果發生了,就能得到相交的引數t。
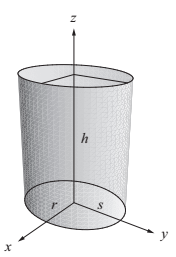
2.4 光線與圓柱體的相交
橢圓柱體側表面x軸方向的半徑為r,y軸方向的半徑為s,高度為h,中心落在x,y平面的原點。它可以由以下方程描述: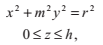
其中m = r/s。如果r = s,那麼這個圓柱體就是圓形的,並且m=1.我們用光線方程P(t)的分量替換原方程中的x,y,得到
展開平方,並以t為主元合併同類項,得到以下這個二次方程:
和球體一樣,這個判別式指出了相交是否會發生。這個方程的解給了我們光線和這個在z軸上無限延展的圓柱面的交點值,我們必須檢測交點的z軸分量是否滿足0<= z < = h。
在碰撞檢測這一章節,問題在於我們需要知道一個移動的球體是否與表達多面體模型的一條線段相交。這個問題可以被轉換為一條光線與給定半徑和任意端點的圓柱體是否相交。這一內容在第12章中介紹。
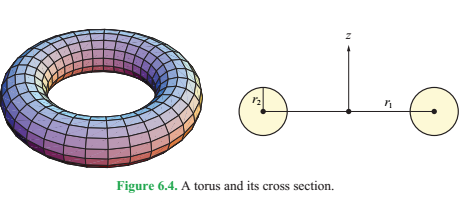
2.5 光線與圓環的相交
圓環的橫截面有一個主半徑r1和一個次半徑r2,如下圖。半徑為r1的圓處在x,y平面上;半徑為r2的圓的圓心落在前一個圓上,並且與它垂直,它是繞著z軸旋轉分佈的。這個旋轉的圓可以用這樣的等式來表達:
其中s的值表達了到x,y平面上的大圓的距離:
我們把這個式子代入前面的表示式,得到:
我們把根式分離,然後再平方,得到圓環體的式子:
把光線方程P(t)的x,y,z分量代入這個式子,得到:
適當的代數簡化後,我們可以用這個四次方程來表達:
其中
同除a使得首項係數化為1,這個方程可以用我們前面提到的四次方程求解方法解決。如果向量V是標準化的,那麼就沒有必要除以a,b和c的計算可以被簡化為:
3.法線計算
有時候用隱函式f(x,y,z)可以更方便的表達一個表面,所有在表面上的點(x,y,z)在函式中的值都為0,所有不在表面上的點的值都不是0。例如,對於橢圓而言,這個函式是這樣的:
使用隱函式表達,我們可以得到一個求表面頂點法線方向的通用計算公式。
設f(x,y,z)表達一個表面S,所以f(x,y,z) = 0就指代表面上所有的點。我們令C為表面上的任一曲線,它由引數方程x(t),y(t)以及z(t)刻畫。那麼,曲線C在點(x(t),y(t),z(t))的切向量T可以表達為:
由於C是表面S上的曲線,T也是表面S的切線。同樣,由於f(x(t),y(t),z(t)) = 0 對於任意t都成立,我們知道在曲線C上,總有df/dt = 0.使用鏈式規則,我們可以寫成:
因為它與T的點乘也是0,向量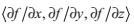
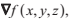
繼續討論上面的方程,對於一個橢球面而言,我們的法線形式為:
4.反射和折射向量
當一束光與物體的表面相撞時,它的部分能量被物體表面吸收,部分能量從表面反射回去,部分能量穿過了物體自身。下一章將會詳細講述這些影響。這一章將著重解釋當光線和一個光澤的或者透明的表面相交時,反射以及折射的方向。4.1 反射向量計算
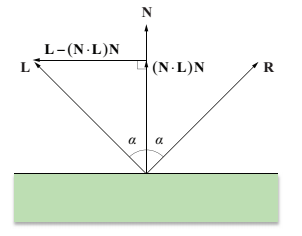
光照射到反光面(如鏡子)的反射方向遵循這樣一個簡單的規則:入射角等於反射角。正如下圖所顯示的,這也就等價於,法線和入射光方向L的夾角等於法線N與反射光方向R的夾角。 我們假設向量N和L都已經標準化到單位長度了。為了得到一個用入射方向L和法線N表達的反射方向公式,我們首先計算出L在與法線N垂直方向的分量: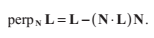 向量R處在向量L與其在法線上的投影的距離的兩倍處,我們可以這樣表達R:
向量R處在向量L與其在法線上的投影的距離的兩倍處,我們可以這樣表達R:
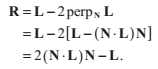
4.2 折射向量計算
透明表面有一個性質叫做折射率。根據斯涅爾定律,入射角和折射角的關係由以下方程表示: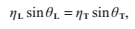 其中
其中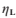 是光線將離開的材料的折射率,
是光線將離開的材料的折射率,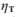 是光線即將進入的材料的折射率。空氣的折射率通常為1。更高的折射率就會在兩個材料的交界處產生更強的彎曲效果。
我們假設法線向量N以及入射光線L都已經標準化到單位長度。我們用法線的垂直和平行分量來表達透射光的方向T,正如下圖顯示的,T關於法線的平行分量表達為
是光線即將進入的材料的折射率。空氣的折射率通常為1。更高的折射率就會在兩個材料的交界處產生更強的彎曲效果。
我們假設法線向量N以及入射光線L都已經標準化到單位長度。我們用法線的垂直和平行分量來表達透射光的方向T,正如下圖顯示的,T關於法線的平行分量表達為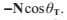 ,垂直分量表達為
,垂直分量表達為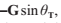 ,其中向量G是與
,其中向量G是與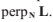 平行的單位向量。由於L是單位長度的,
平行的單位向量。由於L是單位長度的,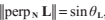 ,所以:
,所以:
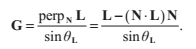
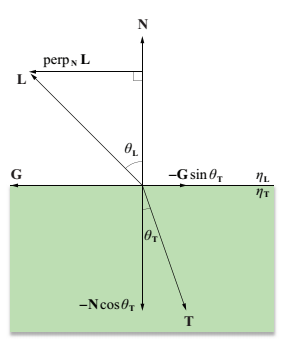 現在,我們可以這樣表示折射向量T:
現在,我們可以這樣表示折射向量T:
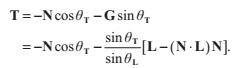 代入折射公式,我們可以替換sin:
代入折射公式,我們可以替換sin:
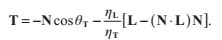 我們用
我們用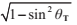 代替
代替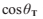 ,然後再次使用折射公式代替sin,我們得到:
,然後再次使用折射公式代替sin,我們得到:
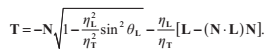 用
用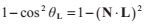 代替
代替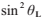 ,最終得到:
,最終得到:
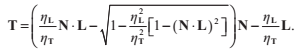 如果
如果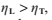 ,那麼根號裡的式子可能是負的,這種情況發生在光線從高折射率媒介到低折射率媒介產生寬入射角時。特別地,方程僅在
,那麼根號裡的式子可能是負的,這種情況發生在光線從高折射率媒介到低折射率媒介產生寬入射角時。特別地,方程僅在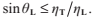 時成立。如果根號裡的式子是負的,那麼說明發生了全反射。這意味著,光線沒有折射,而是發生了反射。
時成立。如果根號裡的式子是負的,那麼說明發生了全反射。這意味著,光線沒有折射,而是發生了反射。