卷積與反捲積詳解
下面是暑期報告PPT的一個截圖展示,是對於卷積與反捲積的具體理解,標題如下:
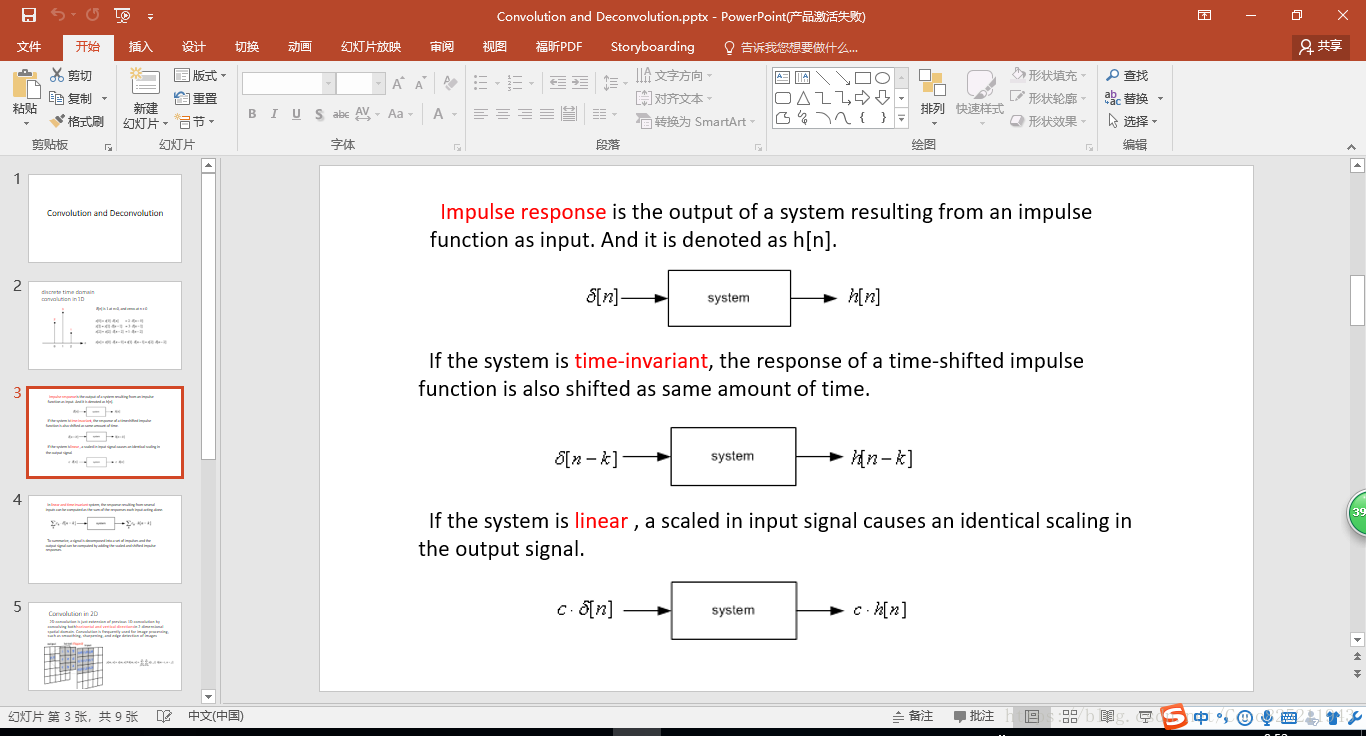
首先先從一維的離散形式出發,可以類比於訊號處理中的德爾塔函式。
這裡說明的是訊號系統的線性不變形,即經過作用函式以後,線性不變,位移不變。
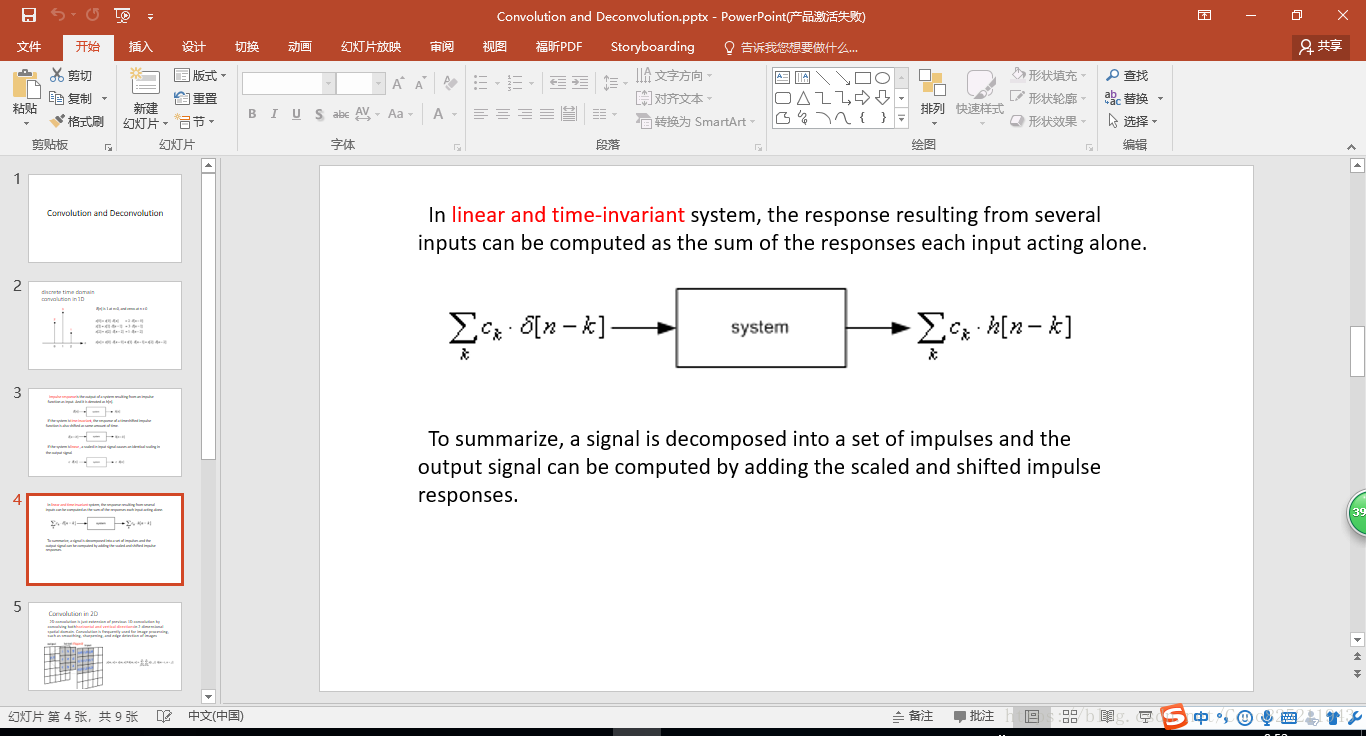
把線性不變性質與位移不變性質(又可以理解成時間不變性,在訊號處理過程中),結合起來可以得到下式:
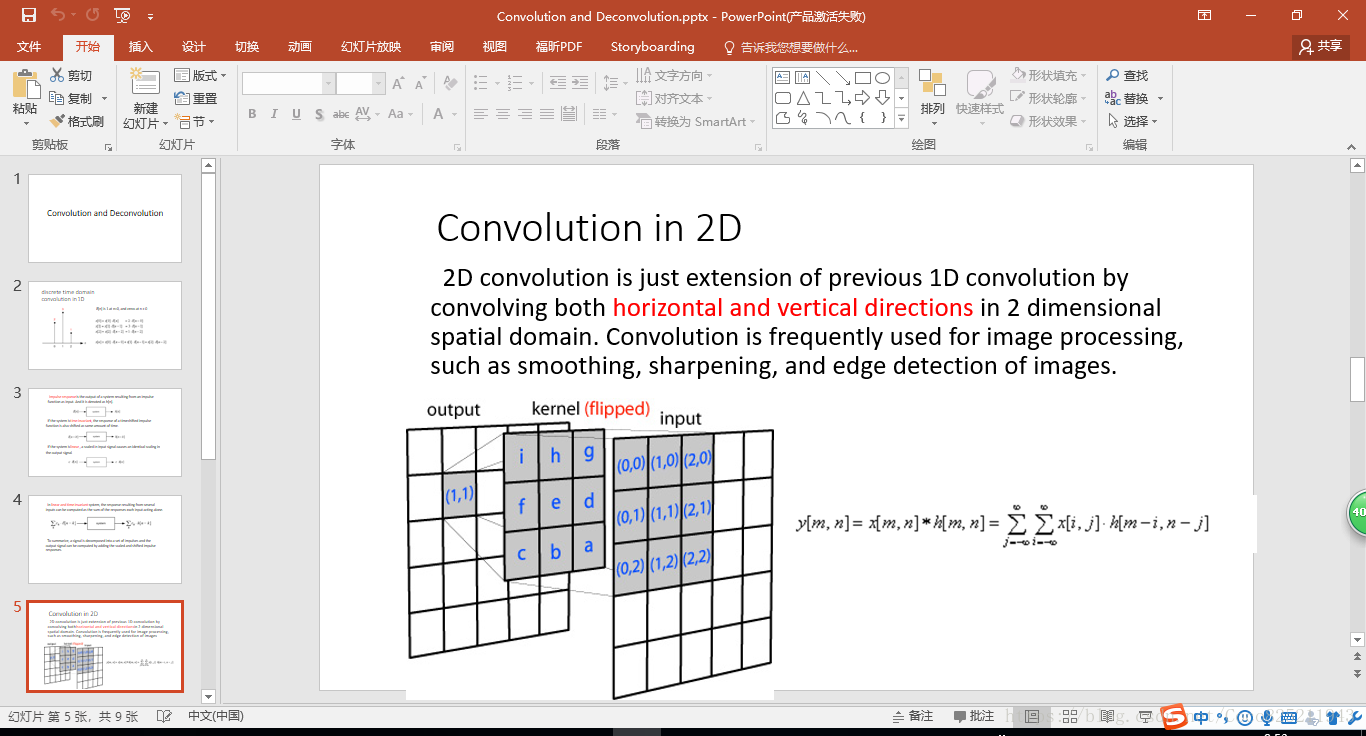
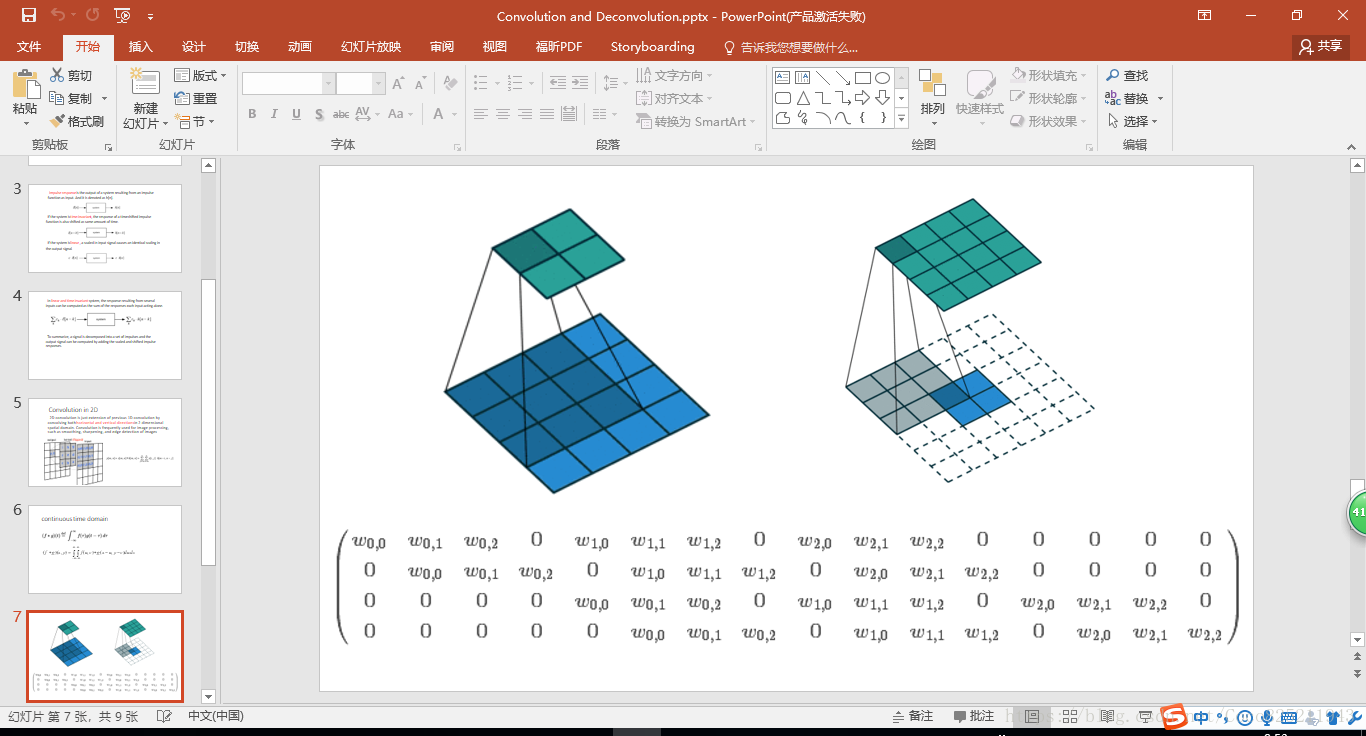
推廣到二維空間中(卷積與反捲積均在二維空間中存在)
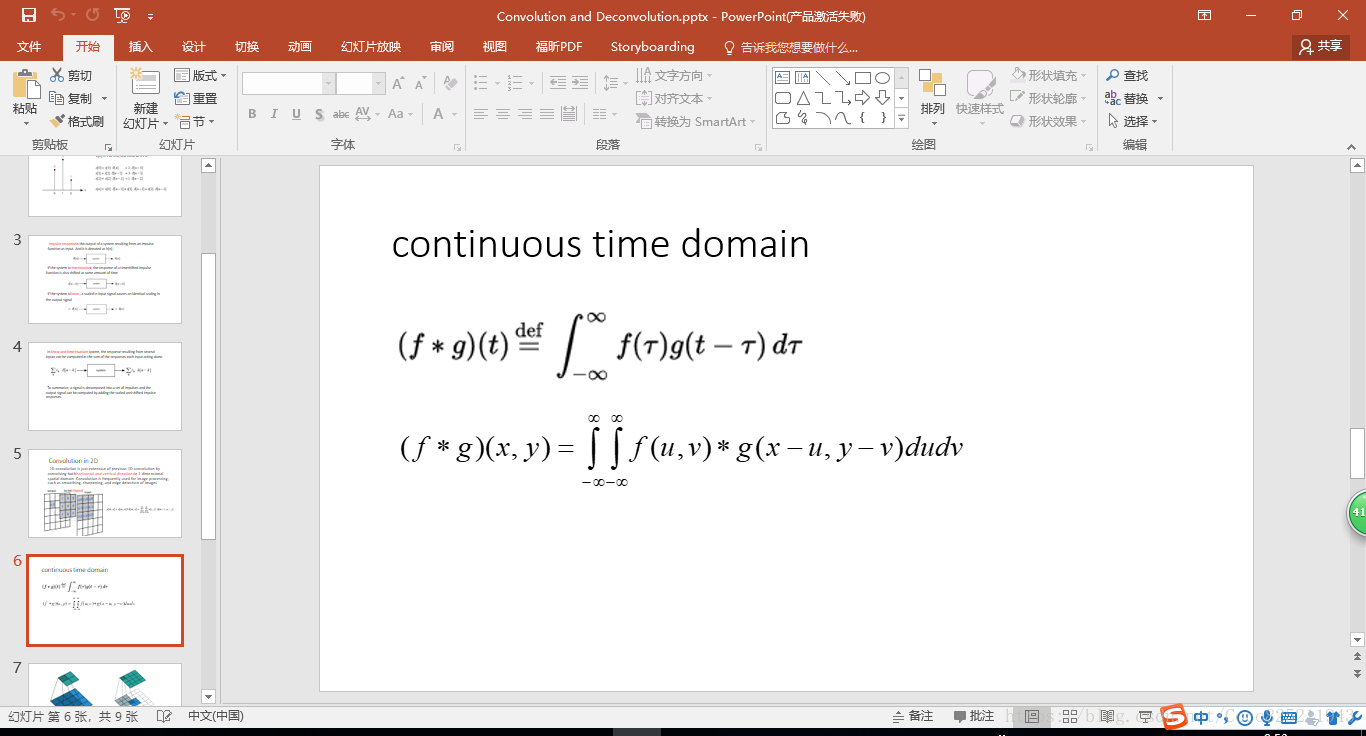
在離散域上式求和,而在連續域上是求積分。
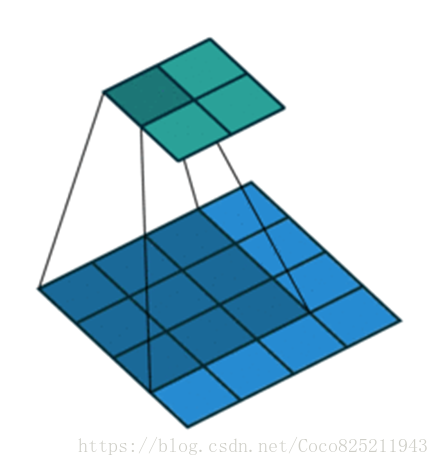
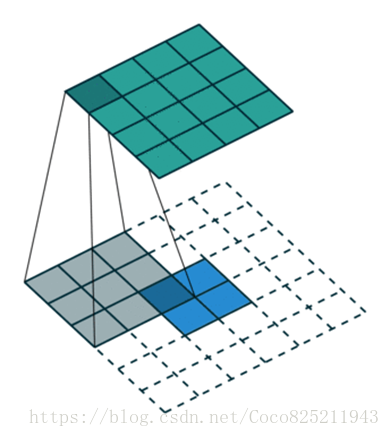
下面是卷積與反捲積的兩個動圖,可以讓我們更好的理解其工作過程。
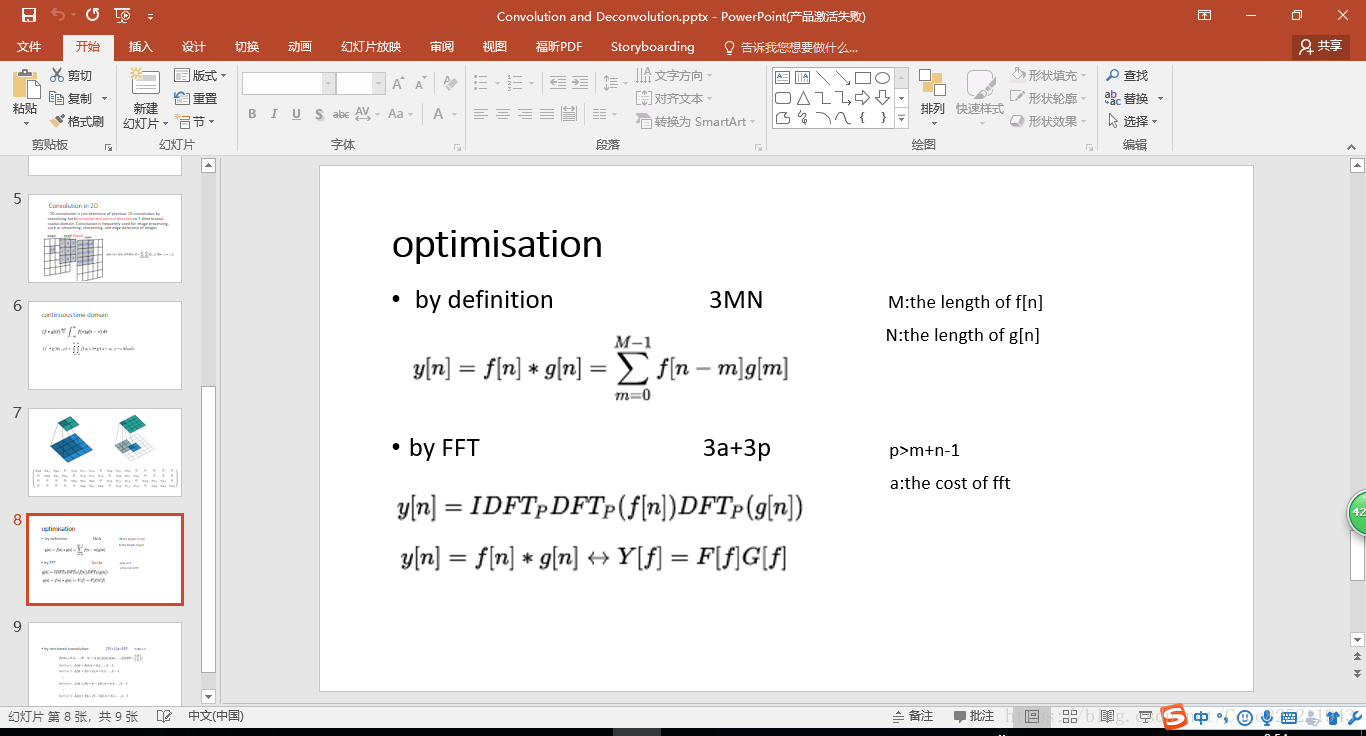
複雜度估算:
相關推薦
卷積與反捲積詳解
下面是暑期報告PPT的一個截圖展示,是對於卷積與反捲積的具體理解,標題如下: 首先先從一維的離散形式出發,可以類比於訊號處理中的德爾塔函式。 這裡說明的是訊號系統的線性不變形,即經過作用函式以後,線性不變,位移不變。 把線性不變性質與位移不變性質(又可以理解
空洞卷積與反捲積
空洞卷積(dilated conv),也稱擴張卷積。空洞卷積可以在kernel有效增大感受野的同時不增加模型引數或者計算量。在影象需要全域性資訊或者語音文字需要較長的sequence資訊依賴的問題中,都能較好的應用空洞卷積。在影象分割,語音合成WaveNet,機器翻譯ByteNet中都有
卷積與反捲積 步長(stride)與重疊(overlap)及 output 的大小
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
卷積神經網路CNN(1)——影象卷積與反捲積(後卷積,轉置卷積)
1.前言 傳統的CNN網路只能給出影象的LABLE,但是在很多情況下需要對識別的物體進行分割實現end to end,然後FCN出現了,給物體分割提供了一個非常重要的解決思路,其核心就是卷積與反捲積,所以這裡就詳細解釋卷積與反捲積。 對於1維的卷積,公式(離散
深度學習中的卷積與反捲積
卷積與反捲積操作在影象分類、影象分割、影象生成、邊緣檢測等領域都有很重要的作用。為了講明白這兩種操作,特別是反捲積操作,本文將依照神經網路中的編碼器——>解碼器——>卷積——>反捲積 的思路來一步步介紹。 編碼器與解碼器 神經網路本質
深度學習---影象卷積與反捲積(最完美的解釋)
動態圖1.前言 傳統的CNN網路只能給出影象的LABLE,但是在很多情況下需要對識別的物體進行分割實現end to end,然後FCN出現了,給物體分割提供了一個非常重要的解決思路,其核心就是卷積與反捲積,所以這裡就詳細解釋卷積與反捲積。 對於1維的卷積,公式(離散
卷積與反捲積的理解
在文章: Fully Convolutional Networks for Semantic Segmentation 網址:https://arxiv.org/abs/1411.4038 中有下面的一段話: 3.3. Upsampling is bac
反捲積與反捲積核的初始化問題
導論: https://blog.csdn.net/qq_30638831/article/details/81532892 https://cv-tricks.com/image-segmentation/transpose-convolution-in-tensor
對深度可分離卷積、分組卷積、擴張卷積、轉置卷積(反捲積)的理解
轉自:https://blog.csdn.net/chaolei3/article/details/79374563 參考: https://zhuanlan.zhihu.com/p/28749411 https://zhuanlan.zhihu.com/p/28186
[CNN] 卷積、反捲積、池化、反池化
之前一直太忙,沒時間整理,這兩天抽出點時間整理一下卷積、反捲積、池化、反池化的內容,也希望自己對一些比較模糊的地方可以理解的更加清晰。 一、卷積 1、卷積的簡單定義 卷積神經網路中的卷積操作可以看做是輸入和卷積核的內積運算。其運算過程非常容易理解,下面有舉例。 2、舉例解
深度學習之卷積和反捲積tensorflow
ps 零零總總接觸深度學習有1年了,雖然時間是一段一段的。現在再拾起來做一個新的專案,有些東西又要重新理解,感覺麻煩。現在就再次學習時候有些困惑的地方捋一遍。 1.卷積 說到卷積,我現在還有印象的是大學裡《訊號與系統》和《數字訊號處理》兩書中的離散訊號的卷積。簡單來你說就是一個訊號固定,一個
神經網路中的卷積和反捲積原理
一.卷積 在深度學習的過程中,很多神經網路都會用到各種卷積核來進行操作,那麼我們就簡單講一下卷積的原理和實現過程。 那麼卷積在神經網路中的作用是什麼呢?一開始的傳統神經網路是沒有卷積層的,都是隱藏層加生全連線層的結構,這樣在中間得到的特徵都是線性的,不能提取到一個區域性的特徵。而卷積
卷積、反捲積、轉置卷積和微步幅卷積
卷積 首先定義本文要用到的符號 輸入圖片的大小: i1=i2=i。 卷積核的大小: k1=k2=k。 卷積步長:s1=s2=s。 填充padding=p。 下圖表示引數為(i=5,k=3,s=2,p=1)的卷積計算過程,可以看出輸出的圖片大小是(3∗3
Kubernetes K8S之affinity親和性與反親和性詳解與示例
Kubernetes K8S之Node節點親和性與反親和性以及Pod親和性與反親和性詳解與示例 主機配置規劃 伺服器名稱(hostname)系統版本配置內網IP外網IP(模擬) k8s-master CentOS7.7 2C/4G/20G 172.16.1.110 1
個人總結:關於tf.nn.conv2d(卷積)與tf.nn.conv2d_transpose(反捲積)的區別
官網中對於卷積tf.nn.conv2d的描述 tf.nn.conv2d( input, filter, strides, padding, use_cudn
深度學習:卷積,反池化,反捲積,卷積可解釋性,CAM ,G_CAM
憑什麼相信你,我的CNN模型?(篇一:CAM和Grad-CAM):https://www.jianshu.com/p/1d7b5c4ecb93 憑什麼相信你,我的CNN模型?(篇二:萬金油LIME):http://bindog.github.io/blog/2018/02/11/model-ex
反捲積、上取樣、上池化的聯絡與區別
FCN於反捲積(Deconvolution)、上取樣(UpSampling) https://blog.csdn.net/nijiayan123/article/details/79416764 反捲積(Deconvolution)、上取樣(UNSampling)與上池化(UnPooling
深度學習基礎--卷積--反捲積(deconvolution)
反捲積(deconvolution) 這個概念很混亂,沒有統一的定義,在不同的地方出現,意義卻不一樣。 上取樣的卷積層有很多名字: 全卷積(full convolution), 網路內上取樣( in-network upsampling), 微步幅卷積(fractio
反捲積(deconvolution)的理解 +上取樣(UNSampling)與上池化(UnPooling)
像往常一樣,舉個梯子: https://blog.csdn.net/A_a_ron/article/details/79181108 上取樣( (UNSampling)與上池化(UnPooling) https://www.zhihu.com/question/436
輕鬆理解轉置卷積(transposed convolution)/反捲積(deconvolution)
原文地址:Up-sampling with Transposed Convolution 在CNN中,轉置卷積是一種上取樣(up-sampling)的方法.如果你對轉置卷積感到困惑,那麼就來讀讀這篇文章吧. 本文的notebook程式碼在Github. 上取樣的需要 在