前向演算法（Forward Algorithm）（二）
計算觀察序列的概率（Finding the probability of an observed sequence）
2b.計算t=1時的區域性概率
’s
我們按如下公式計算區域性概率：
t ( j )= Pr( 觀察狀態 | 隱藏狀態j ) x Pr(t時刻所有指向j狀態的路徑）
特別當t=1時，沒有任何指向當前狀態的路徑。故t=1時位於當前狀態的概率是初始概率，即Pr(state|t=1)=P(state)，因此，t=1時的區域性概率等於當前狀態的初始概率乘以相關的觀察概率：
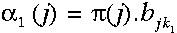
所以初始時刻狀態j的區域性概率依賴於此狀態的初始概率及相應時刻我們所見的觀察概率。
2c.計算t>1時的區域性概率
我們再次回顧區域性概率的計算公式如下：
t ( j )= Pr( 觀察狀態 | 隱藏狀態j ) x Pr(t時刻所有指向j狀態的路徑）我們可以假設（遞迴地），乘號左邊項“Pr( 觀察狀態 | 隱藏狀態j )”已經有了，現在考慮其右邊項“Pr(t時刻所有指向j狀態的路徑）”。
為了計算到達某個狀態的所有路徑的概率，我們可以計算到達此狀態的每條路徑的概率並對它們求和，例如：
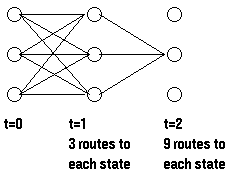
計算
所需要的路徑數目隨著觀察序列的增加而指數級遞增，但是t-1時刻’s給出了所有到達此狀態的前一路徑概率，因此，我們可以通過t-1時刻的區域性概率定義t時刻的’s，即：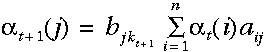
故我們所計算的這個概率等於相應的觀察概率（亦即，t+1時在狀態j所觀察到的符號的概率）與該時刻到達此狀態的概率總和——這來自於上一步每一個區域性概率的計算結果與相應的狀態轉移概率乘積後再相加——的乘積。
注意我們已經有了一個僅利用t時刻區域性概率計算t+1時刻區域性概率的表示式。
現在我們就可以遞迴地計算給定隱馬爾科夫模型(HMM)後一個觀察序列的概率了——即通過t=1時刻的區域性概率
’s，通過t=2時刻的’s計算t=3時刻的’s等等直到t=T。給定隱馬爾科夫模型(HMM)的觀察序列的概率就等於t=T時刻的區域性概率之和。
2d.降低計算複雜度
我們可以比較通過窮舉搜尋（評估）和通過遞迴前向演算法計算觀察序列概率的時間複雜度。
我們有一個長度為T的觀察序列O以及一個含有n個隱藏狀態的隱馬爾科夫模型l=(
,A,B)。
窮舉搜尋將包括計算所有可能的序列：
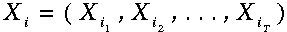
公式
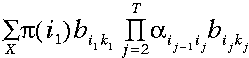
對我們所觀察到的概率求和——注意其複雜度與T成指數級關係。相反的，使用前向演算法我們可以利用上一步計算的資訊，相應地，其時間複雜度與T成線性關係。
注：窮舉搜尋的時間複雜度是
，前向演算法的時間複雜度是
3.總結
我們的目標是計算給定隱馬爾科夫模型HMM下的觀察序列的概率——Pr(observations |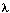
)。
我們首先通過計算區域性概率（’s）降低計算整個概率的複雜度，區域性概率表示的是t時刻到達某個狀態s的概率。
t=1時，可以利用初始概率(來自於P向量）和觀察概率Pr(observation|state)（來自於混淆矩陣）計算區域性概率；而t>1時的區域性概率可以利用t-時的區域性概率計算。
因此，這個問題是遞迴定義的，觀察序列的概率就是通過依次計算t=1,2,…,T時的區域性概率，並且對於t=T時所有區域性概率’s相加得到的。
注意，用這種方式計算觀察序列概率的時間複雜度遠遠小於計算所有序列的概率並對其相加（窮舉搜尋）的時間複雜度。