0 前言

2018年7月到9月，我做一個專案，Python程式設計實現。Python程式寫出來了，但是很慢。Python的for loop真是龜速呀。這個程式的瓶頸部分，就是一個雙層for loop，內層for loop裡是矩陣乘法。於是乎想到了numba來給瓶頸部分做優化。簡單的@numba.jit可以加速幾十倍，但是很奇怪無法和joblib配合使用。

最終解決方案是使用@numba.cuda.jit，他可以輕鬆加速數千倍 — 這篇部落格就帶你入門GPU程式設計，本文出了闡述我對於GPU程式設計的理解和小結，還引用了一些非常好的學習資料。我這裡說的GPU，專門指的是NVIDIA GPU的CUDA程式設計。

1 GPU 程式設計思想

傳統意義上來講，大部分程式是執行在CPU上的，GPU只是玩遊戲的時候派上用場。然而現在GPU的重要性大幅度提升，NVIDIA的股票也是高速上漲，因為GPU除了遊戲，增加了一個killer app：機器學習。另外，比特幣挖礦也是要用GPU的。

1. 編寫CPU的程式，有兩個特點：單執行緒思想，面向物件思想。
2. 編寫GPU的程式，有兩個特點：千執行緒思想，面向陣列思想。

1.1 千執行緒思想

CPU當然也有多執行緒程式，比如我的Macbook Pro是雙核四執行緒，可以同時跑四個執行緒。但是CPU的多執行緒和GPU的多執行緒有兩點本質區別：1）CPU的“多”，規模是十，然而GPU的“多”，規模是千

圖1：本圖和下文很多圖片，來自這個連結

進一步解釋第二點，假設一個$function$內部是一個雙層for loop i := 0 $\cdots$ 999，程式需要呼叫四次$function$。那麼CPU的程式會同時搞出四個執行緒，每個執行緒呼叫一次function，每次順序執行for loop$1000^2$次。而GPU的騷操作是，順序呼叫四次function，每次搞出$1000^2$個執行緒一下子解決這個雙層for loop。當然了，你需要改寫程式，改為$f$

這裡申明很重要一點，不是所有的$function$能(適合)改寫為$function\_gpu$。不過很多機器學習相關的演算法，很多計算密集行演算法，是可以改寫的。會把$function$改寫為$function\_gpu$是一種當下少數人掌握的技能。在本文chapter 3將講解幾乎是的GPU程式設計的Hello world。

1.2 面向陣列思想

面向物件的程式設計思想是當下主流思想：一個物件有若干個屬性，一個容器裝很多個物件，如果想獲取物件的屬性，需要獲取物件然後進行點操作。面向陣列則完全不同。在做data science(DS) 和 machine learning(ML) 專案的時候，都是面向陣列的思想。Numpy.ndarray和Pandas.DataFrame都是設計的非常棒的”超級陣列"。

在DS和ML專案裡面，陣列之所以作為唯一欽定的資料結構，我認為是陣列能夠完美勝任DS和ML 專案裡面組織和管理資料的工作。DS和ML專案完全不需要object-oriented的那一套封裝和繼承的思想，也不需要連結串列、棧、佇列、雜湊表、二叉樹、B-樹、圖等其他資料結構。這背後的原因，我認為是DS和ML專案和那種企業級開發存在天然的區別。比如企業級開發需要處理複雜的業務邏輯，DS和ML專案就沒有複雜的業務邏輯，只有對數組裡的資料的反覆“暴力計算”，這種對一個數組裡的資料進行反覆的暴力計算，正好是GPU說擅長的東西，SIMD(single instruction multiple data)既視感。

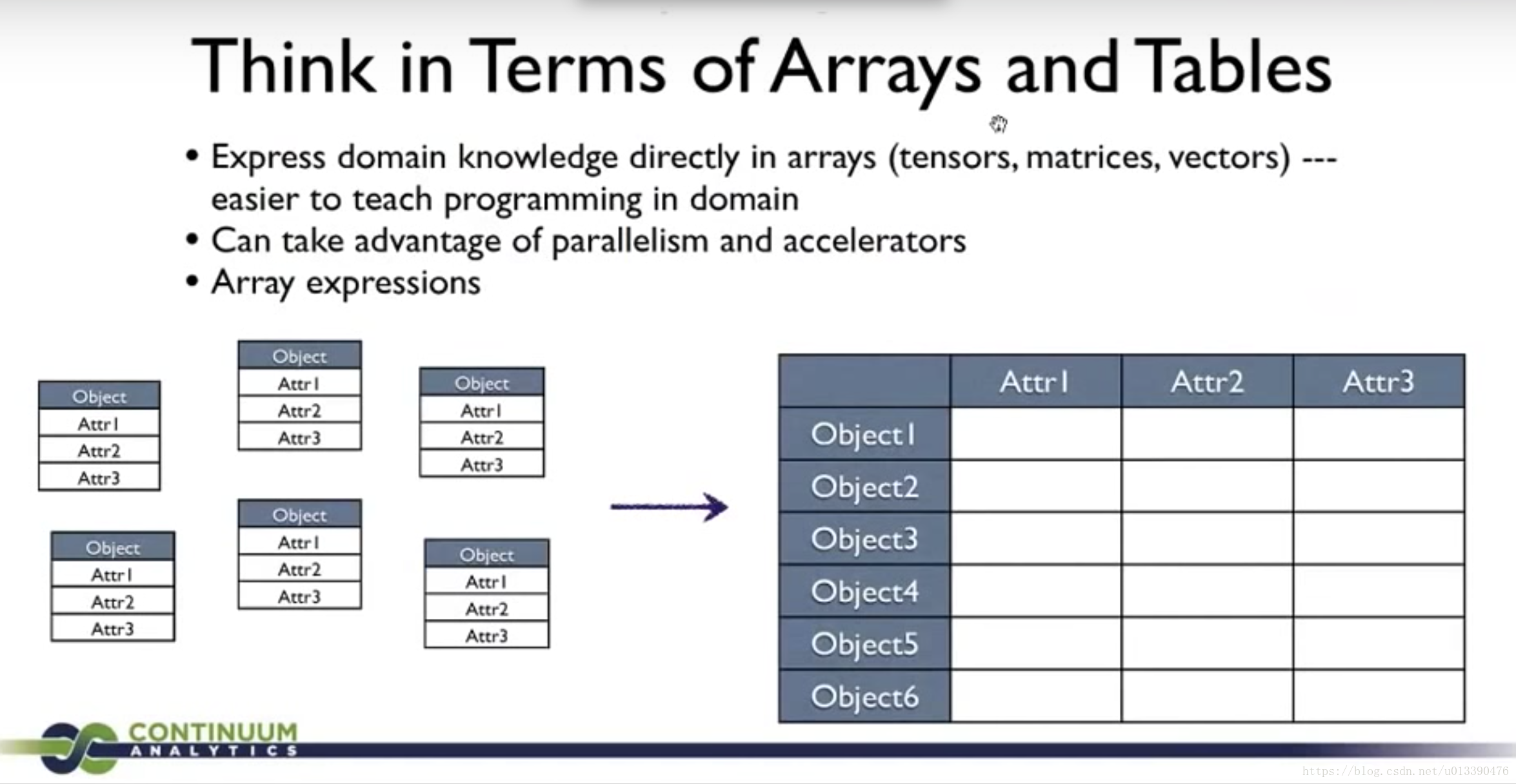
圖2：截圖自這個YouTube視訊。

所以我在使用GPU加速的方法來對程式進行改造的時候，寫了一個def to_array(self) 的方法，就是為了把物件的資料轉移到numpy array裡面去。

2 圖解GPU

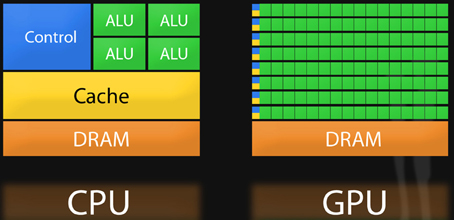
圖3：CPU裡面有很大的快取(黃色)，GPU裡面快取很少。CPU擅長複雜的程式控制(藍色)，但是ALU算術運算單元(綠色)比較少。GPU最大的特點就是ALU很多，擅長算數計算。

圖4：GPU加速的方法是，把程式裡面計算密集型的CPU程式碼，改寫為GPU程式碼。讓CPU做CPU擅長的事情，讓GPU做GPU擅長的事情，優勢互補。

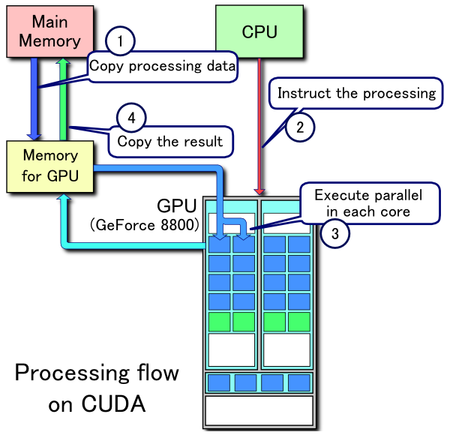
圖5：GPU是如何和記憶體和CPU相配合的，分為4個步驟。其中步驟1和4是很消耗時間的，實際程式設計的時候，需要考慮如何減少1和4。

圖6：CUDA是這樣子組織上千個執行緒的，若干執行緒匯聚為一個block，若干block匯聚為一個grid。這就是CUDA的two-level thread hierarchy。深刻理解這個two-level對於編寫CUDA程式十分重要。

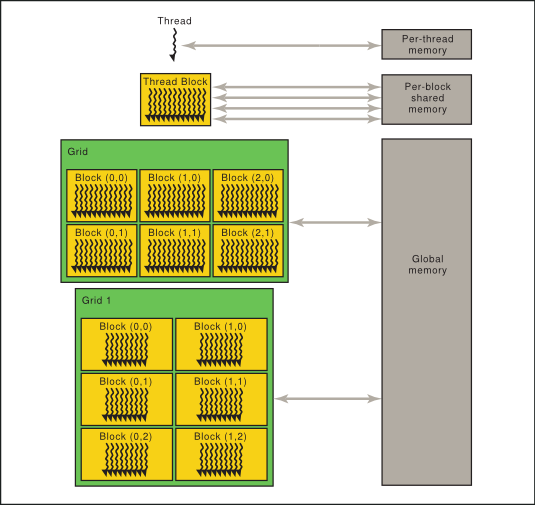
圖7：GPU的記憶體模型。GPU裡面的記憶體分為三種：per thread local memory， per block shared memory，和global memory。在實際程式設計的時候，需要考慮多用shared memory，少用global memory，因為shared比global的訪問和存取速度快很多。

3 GPU的Hello world: 矩陣相乘

能夠讓人理解GPU程式設計的 Hello world 程式，便是矩陣相乘。這個紐約大學的教程非常棒，詳細講解了如何編寫GPU程式進行矩陣相乘。我當時學習Numba和CUDA，這個教程發揮了很大的作用。

3.1介紹幾個名詞

首先，要弄清楚下面6個名詞的概念。編寫GPU程式，其實是一種CPU和GPU之間的“互動”，所謂的異構開發。

1. Host。代表CPU。
2. Device。代表GPU。
3. Host memory。RAM記憶體。
4. Device memory。GPU上的儲存。
5. Kernal function。GPU函式，執行在device上面，呼叫者是host。
6. Device function。GPU函式，執行在device上面，呼叫者是kernal function或者device function。

3.2 GPU程式的執行流程

圖5可視化了GPU程式的流程：

1. 把陣列的資料(numpy.ndarray)從host memory拷貝到device memory上。
2. 配置kernal function的引數，呼叫kernal function。引數有兩種：一種用中括號[ ]，一種用小括號( )。中括號的引數是threadperblock和blockpergrid，參考圖6。小括號就是那種普通函式的引數。
3. 幾千個執行緒同時呼叫同一個kernal function，在GPU裡面進行計算。kernal function的編寫，是一門技術。
4. 把GPU裡面的運算結果，從device memory拷貝回host memory。THE END。

3.3 矩陣相乘原始碼

這份Python程式碼，有6個函式，進行 $\mathbf{C} = \mathbf{A} \times \mathbf{B}$

1. cpu_mat_mul(A, B, C), 基於CPU的矩陣相乘，$O(n^3)$。
2. cpu_mat_mul_jit(A, B, C)，和cpu_mat_mul相比，唯一的區別就是加了裝飾器 @jit，這是一種編譯優化工具，可以加快幾十倍。
3. mat_mul_naive_kernal(A, B, C)，矩陣相乘的GPU函式，使用global memory。
4. mat_mul_shared_kernal(A, B, C)，矩陣相乘的GPU，使用了shared memory。shared memory比global memory訪問速度快不少。
5. host_naive(A, B, C)，mat_mul_naive_kernal的“配套設施”，kernal不能獨立存在的，前前後後需要一些程式碼輔助。
6. host_optimized(A, B, C)，mat_mul_shared_kernal的“配套設施”。如果host_naive比cpu_mat_mul快三千倍的話，host_optimized可能快三千五百倍。

我在學習Numba CUDA的時候，使用的Anaconda Python3.6，Numba 0.38， cudatoolkit 9.0。

'''
Matrix multiplication sample, some numba and CUDA testing code
'''
import math
import time
import numpy as np
from numba import cuda, jit, float64

TPB = 16 # thread per block

def cpu_mat_mul(A, B, C):
    '''matrix mulplication on cpu, O(n^3) implementation
    '''
    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            summation = 0
            for k in range(A.shape[1]):
                summation += A[i, k] * B[k, j]
            C[i, j] = summation

@jit
def cpu_mat_mul_jit(A, B, C):
    '''matrix mulplication on cpu O(n^3) implementation with @jit decocation
    '''
    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            summation = 0
            for k in range(A.shape[1]):
                summation += A[i, k] * B[k, j]
            C[i, j] = summation

@cuda.jit
def mat_mul_naive_kernal(A, B, C):
    '''matrix multiplication on gpu, naive method using global device memory
    '''
    i, j = cuda.grid(2)
    if i < C.shape[0] and j < C.shape[1]:
        summation = 0
        for k in range(A.shape[1]):
            summation += A[i, k] * B[k, j]
        C[i, j] = summation

@cuda.jit
def mat_mul_shared_kernal(A, B, C):
    '''matrix multiplication on gpu, optimized version using shared memory.
    '''
    s_A = cuda.shared.array((TPB, TPB), dtype=float64)  # s_ --> shared
    s_B = cuda.shared.array((TPB, TPB), dtype=float64)
    x, y = cuda.grid(2)
    tx = cuda.threadIdx.x
    ty = cuda.threadIdx.y
    bw = cuda.blockDim.x
    bh = cuda.blockDim.y
    #print((x, y), (tx, ty), (bx, by), (bw, bh))

    if x >= C.shape[0] or y >= C.shape[1]:
        return

    tmp = 0
    for i in range(int(A.shape[1]/TPB)):
        #print((x, y), (tx, ty), i)
        s_A[tx, ty] = A[x, ty + bw*i]
        s_B[tx, ty] = B[tx + bh*i, y]
        cuda.syncthreads()

        for j in range(TPB):
            tmp += s_A[tx, j] * s_B[j, ty]

        cuda.syncthreads()
    C[x, y] = tmp


def host_naive(A, B, C):
    '''host code for calling naive kernal
    '''
    d_A = cuda.to_device(A)  # d_ --> device
    d_B = cuda.to_device(B)
    d_C = cuda.device_array(C.shape, np.float64)

    threadsperblock = (TPB, TPB)
    blockspergrid_x = math.ceil(A.shape[0]/threadsperblock[0])
    blockspergrid_y = math.ceil(B.shape[1]/threadsperblock[1])
    blockspergrid = (blockspergrid_x, blockspergrid_y)

    mat_mul_naive_kernal[blockspergrid, threadsperblock](d_A, d_B, d_C)

    return d_C.copy_to_host()


def host_optimized(A, B, C):
    '''host code for calling naive kernal
    '''
    d_A = cuda.to_device(A)  # d_ --> device
    d_B = cuda.to_device(B)
    d_C = cuda.device_array(C.shape, np.float64)

    threadsperblock = (TPB, TPB)
    blockspergrid_x = math.ceil(A.shape[0]/threadsperblock[0])
    blockspergrid_y = math.ceil(B.shape[1]/threadsperblock[1])
    blockspergrid = (blockspergrid_x, blockspergrid_y)

    mat_mul_shared_kernal[blockspergrid, threadsperblock](d_A, d_B, d_C)

    return d_C.copy_to_host()


def main():
    '''main
    '''
    A = np.full((TPB*4, TPB*6), 0.5, dtype=np.float64)
    B = np.full((TPB*6, TPB*2), 2, dtype=np.float64)
    C = np.full((TPB*4, TPB*2), 0, dtype=np.float64)

    start = time.time()
    cpu_mat_mul(A, B, C)
    print('cpu mat mul:', time.time()-start)

    start = time.time()
    cpu_mat_mul_jit(A, B, C)
    print('cpu mat mul with numba.jit:', time.time()-start)

    start = time.time()
    ans = host_naive(A, B, C)
    print('gpu mat mul global:', time.time()-start)
    print(ans)
    
    start = time.time()
    ans = host_optimized(A, B, C)
    print('gpu mat mul shared:', time.time()-start)
    print(ans)

if __name__ == '__main__':
    main()

3.4 理解GPU的矩陣相乘演算法的關鍵

$\mathbf{C} = \mathbf{A} \times \mathbf{B}$
假設A.shape = (64, 96), B.shape = (96, 32)，那麼C.shape = (64, 32)，即C矩陣有2048個元素。

1. CPU的演算法，是1個執行緒，順序依次計算2048個元素的值。
2. GPU的演算法，是同時開出2048個執行緒，每個執行緒計算一個元素的值。執行緒與執行緒之間是並行的。

目前最新的英偉達GeForce RTX 2070，可以同時開出2304個執行緒，2048個執行緒簡直是輕鬆無壓力。

$The\ End$

$喜歡記得點贊喲$