寫在前面

給定一個樣本集，怎麼得到該樣本集的分佈密度函式，解決這一問題有兩個方法：

1.引數估計方法
簡單來講，即假定樣本集符合某一概率分佈，然後根據樣本集擬合該分佈中的引數，例如：似然估計，混合高斯等，由於引數估計方法中需要加入主觀的先驗知識，往往很難擬合出與真實分佈的模型；
2.非引數估計
和引數估計不同，非引數估計並不加入任何先驗知識，而是根據資料本身的特點、性質來擬合分佈，這樣能比引數估計方法得出更好的模型。核密度估計就是非引數估計中的一種，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。Ruppert和Cline基於資料集密度函式聚類演算法提出修訂的核密度估計方法。

直方圖到核密度估計

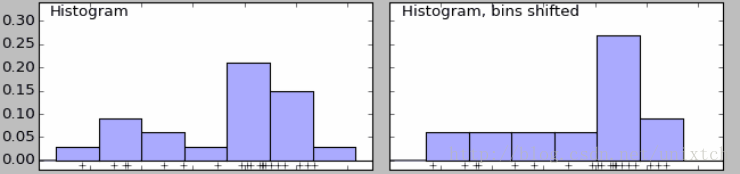
給定一個數據集，需要觀察這些樣本的分佈情況，往往我們會採用直方圖的方法來進行直觀的展現。該方法簡單，容易計算，但繪製直方圖時，需要確定bins，如果bins不同，那麼最後的直方圖會產生很大的差別。如下面的兩直方圖，右邊比左邊的直方圖多劃分了bins，導致最後的結果有很大的差別，左邊時雙峰的，右邊時單峰的。

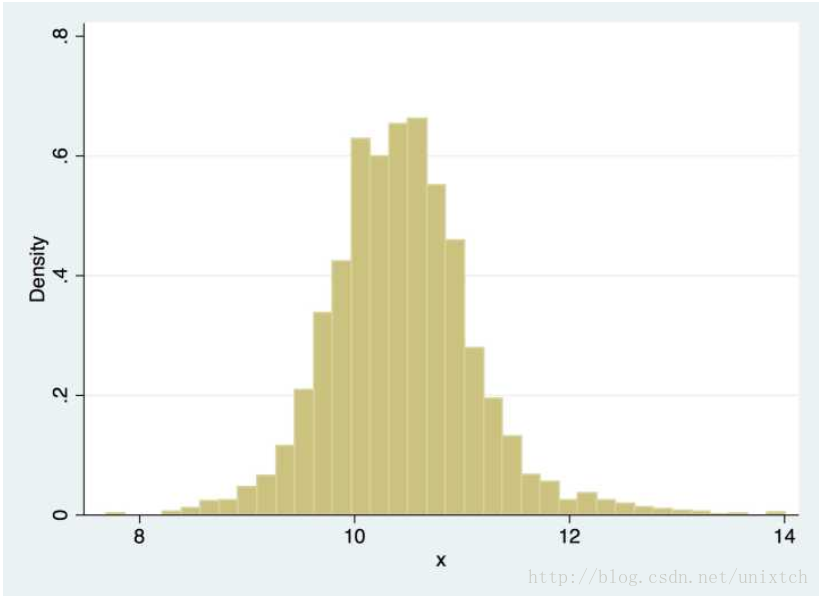
除此之外，直方圖還存在一個問題，那就是直方圖展示的分佈曲線並不平滑，即在一個bin中的樣本具有相等的概率密度，顯然，這一點往往並不適合。解決這一問題的辦法時增加bins的數量，當bins增到到樣本的最大值時，就能對樣本的每一點都會有一個屬於自己的概率，但同時會帶來其他問題，樣本中沒出現的值的概率為0，概率密度函式不連續，這同樣存在很大的問題。如果我們將這些不連續的區間連續起來，那麼這很大程度上便能符合我們的要求，其中一個思想就是對於樣本中的某一點的概率密度，如果能把鄰域的資訊利用起來，那麼最後的概率密度就會很大程度上改善不連續的問題，為了方便觀察，我們看另外一副圖。

現在我們假設要求x處的密度函式值，根據上面的思想，如果取x的鄰域[x-h,x+h]，當h->0的時候，我們便能把該鄰域的密度函式值當作x點的密度函式值。用數學語言寫就是：

f^(x)=12hlimh−>0Nxi∈[x−h,x+h]Ntotal Nxi∈[x−h,x+h]時該鄰域中的樣本點數量，Ntotal樣本集的總數量，最後對該鄰域內的密度值取平均便得到x點的密度函式值f(x)。把上面的式子進行改寫：f^(x)=12hNtotal∑i=x−hx+hxi=1hNtotal∑i|x−xi|2h<1,h−>0 這裡h如果選的太大，肯定不符合h趨向於0的要求。h選的太小，那麼用於估計f(x)的點實際上非常少。這也就是非引數估計裡面的bias-variance tradeoff，也就是偏差和方差的平衡。這樣後還是存在一個問題，那就是概率密度函式依然不夠平滑（因為兩個數之間的存在無數個數啊）。

記K

(x)=121{x<1}，那麼：f^(x)=1hNtotal∑iK(|x−xi|h)由於需要滿足概率密度的積分為1，所以：∫f^(x)=1hNtotal∑i∫K(|x−xi|hdx=1Ntotal∑i∫K(t)dt=∫K(t)dt 也就是要滿足K(t)的積分等於1也就滿足了f^(x)的積分為1。如果把K(t)當作其他已知的概率密度函式，那麼問題就解決了，最後的密度函式也就連續了。

核函式

從支援向量機、meansift都接觸過核函式，應該說核函式是一種理論概念，但每種核函式的功能都是不一樣的，這裡的核函式有uniform,triangular, biweight, triweight, Epanechnikov,normal等。這些核函式的影象大致如下圖：

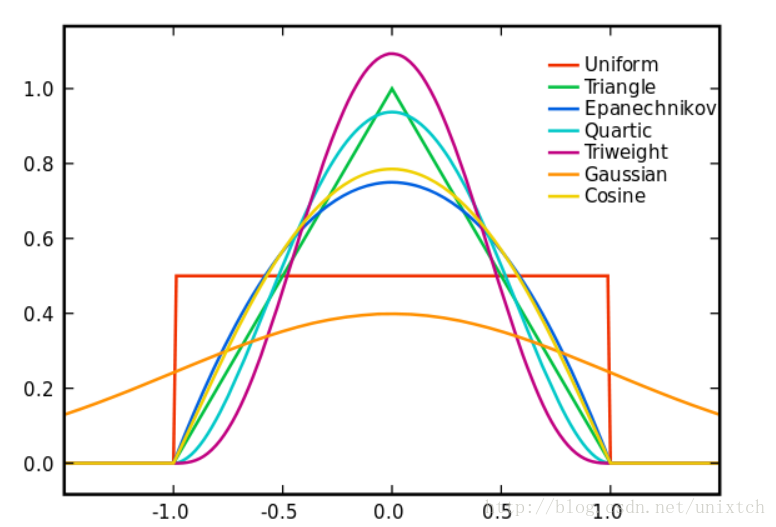
有言論稱Epanechnikov 核心在均方誤差意義下是最優的，效率損失也很小。這一點我沒有深究是如何得到的，暫且相信吧^^。由於高斯核心方便的數學性質，也經常使用 K(x)= ϕ(x)，ϕ(x)為標準正態概率密度函式。
從上面講述的得到的是樣本中某一點的概率密度函式，那麼整個樣本集應該是怎麼擬合的呢？將設有N個樣本點，對這N個點進行上面的擬合過後，將這N個概率密度函式進行疊加便得到了整個樣本集的概率密度函式。例如利用高斯核對X={x1=−2.1,x2=−1.3,x3=−0.4,x4=1.9,x5=5.1,x6=6.2} 六個點的“擬合”結果如下：


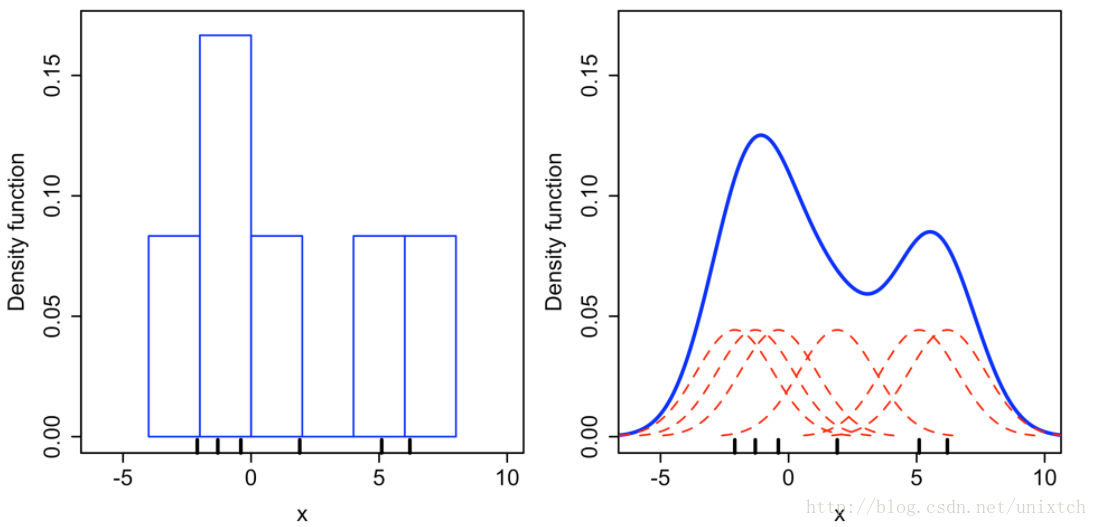
左邊是直方圖，bin的大小為2，右邊是核密度估計的結果。

頻寬的選擇

在核函式確定之後，比如上面選擇的高斯核，那麼高斯核的方差，也就是h（也叫頻寬，也叫視窗，我們這裡說的鄰域）應該選擇多大呢？不同的頻寬會導致最後的擬合結果差別很大。同時上面也提到過，理論上h->0的，但h太小，鄰域中參與擬合的點就會過少。那麼藉助機器學習的理論，我們當然可以使用交叉驗證選擇最好的h。另外，也有一個理論的推導給你選擇h提供一些資訊。
在樣本集給定的情況下，我們只能對樣本點的概率密度進行計算，那擬合過後的概率密度應該核計算的值更加接近才好，基於這一點，我們定義一個誤差函式，然後最小化該誤差函式便能為h的選擇提供一個大致的方向。選擇均平方積分誤差函式(mean intergrated squared error)，該函式的定義是：

MISE(h)=E∫(f^(x)−f(x))2dx 在weak assumptions下，MISE(h)=AMISE(h)+o(

相關推薦

核密度估計Kernel Density Estimation(KDE)

備：密度估計相關知識密度估計經常在統計學中作為一種基於有限的樣本來估計其概率密度函式的方法。在研究隨機變數的過程中，隨機變數的概率密度函式的作用是描述隨機變數的特性。但是在實際應用中，總體概率密度函式通

核密度估計 Kernel Density Estimation(KDE)

寫在前面 給定一個樣本集，怎麼得到該樣本集的分佈密度函式，解決這一問題有兩個方法： 1.引數估計方法 簡單來講，即假定樣本集符合某一概率分佈，然後根據樣本集擬合該分佈中的引數，例如：似然估計，混合高斯等，由於引數估計方法中需要加入主觀的先驗知識，

核密度估計（kernel density estimation）

有一些資料，想“看看”它長什麼樣，我們一般會畫直方圖（Histogram）。現在你也可以用核密度估計。 #什麼是“核” 如果不瞭解背景，看到“核密度估計”這個概念基本上就是一臉懵逼。我們先說說這個核 (kernel) 是什麼。 首先，“核”在不同的語境下的含義是不同的，例如在模式識別裡，它的含義就和這裡不同。

機器學習-直方圖和核密度估計（Kernel Density Estimates）

1、直方圖的問題 ①直方圖裝箱（binning）的過程會導致資訊丟失。 ②直方圖不是唯一的。對比起來比較困難。 ③直方圖不是平滑的 ④直方圖不能很好的處理極值 核密度估計（KDE）完全沒有上述的問題。 構建KDE需要準備核函式：下面是常用的核函式圖形和定義。

核模型（核密度估計）

1、核模型（Kernel function） 線上性模型中，多項式或三角函式等基函式與訓練樣本{（xi,yi）}毫不相關的。下面我們介紹一種模型，在基函式設計的時候會使用到輸入樣本{xi}。 note：是在基函式設計的時候使用到樣本，那麼訓練的是什麼？下面看公式。 核模型，是以

MATLAB中自帶的核密度估計函式

我們在統計資料處理時，經常計算一個樣本的概率密度估計，也就是說給出一組統計資料，要求你繪製出它的概率分佈曲線，matlab的統計工具箱中有直接的函式  就是：Ksdensity 核心平滑密度估計 [f,xi] = ksdensity(x) 計算樣本向量x的概率密度估計

人群密度估計-Crowd Density

一. 應用背景      在安防大背景下，對敏感區域人流量的管控是一個重要的課題，防止人群騷亂、踩踏現象的發生，對非預期的人員匯聚進行預警等等，最常用的方法是檢測到每個目標，然後藉助 Perspective 矩陣完成到實際位置的對映，當然，在目標很難檢測的情況下（密度極大、遮

核密度估計與自適應頻寬的核密度估計

最近看論文，發現一個很不錯的概率密度估計方法。在此小記一下。 先來看看準備知識。 密度估計經常在統計學中作為一種使用有限的樣本來估計其概率密度函式的方法。 我們在研究隨機變數的過程中，隨機變數的概率密度函式的作用是描述隨機變數的特性。（概率密度函式是用來描

非引數估計——核密度估計（Parzen窗）

　　核密度估計，或Parzen窗，是非引數估計概率密度的一種。比如機器學習中還有K近鄰法也是非參估計的一種，不過K近鄰通常是用來判別樣本類別的，就是把樣本空間每個點劃分為與其最接近的K個訓練抽樣中，佔比最高的類別。 直方圖 　　首先從直方圖切入。對於隨機變數$X$的一組抽樣，即使$X$的值是連續的，我們也可以

人群密度估計--Generating High-Quality Crowd Density Maps using Contextual Pyramid CNNs

Generating High-Quality Crowd Density Maps using Contextual Pyramid CNNs ICCV2017 針對人群密度估計問題，本文主要從 incorporating global and loca

車輛密度估計--Understanding Traffic Density from Large-Scale Web Camera Data

Understanding Traffic Density from Large-Scale Web Camera Data CVPR2017 https://arxiv.org/abs/1703.05868 本文介紹了兩個演算法用於車輛密度估計：1）OP

影象處理基礎知識系列之二：核概率密度估計簡介

　　在這裡提出一個問題，假設資料不完整性一致，就是x我們不知道的取值數量是一定的，最後的概率密度估計圖形和什麼有關係呢？和ｂｉｎ有關。bin不同，最後的對應著概率密度估計就不同，如圖5和圖6。這個bin組距引數對應著公式（1）中的h,,,而公式（1）中的n對應著直方圖組數，（組距＝ｂｉｎ＝ｈ，組數＝ｎ）具體關

【MLE】最大似然估計Maximum Likelihood Estimation

like 分布 什麽 9.png 顏色 ... 部分 多少 ati 模型已定，參數未知 最大似然估計提供了一種給定觀察數據來評估模型參數的方法，假設我們要統計全國人口的身高，首先假設這個身高服從服從正態分布，但是該分布的均值與方差未知。我們沒有人力與物力去統計

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之二（作者簡介）

AR aca rtu href beijing cert school start ica Brief Introduction of the AuthorChief Architect at 2Wave Technology Inc. (a startup company

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之一（簡介）

價值 新書 The aar 生成 syn TE keras 第一章 A Gentle Introduction to Probabilistic Modeling and Density Estimation in Machine LearningAndA Detailed

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之五（第3章 之 EM算法）

ado vpd dea bee OS deb -o blog Oz 機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之五（第3章 之 EM算法）

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之六（第3章 之 VI/VB算法）

dac term http 51cto -s mage 18C watermark BE ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之七（第4章 之 梯度估算）

.com 概率 roc 生成 詳解 time 學習 style BE ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?機器學習中的概率模型和概率密度估計方法及V

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之八（第4章 之 AEVB和VAE）

RM mes 9.png size mar evb DC 機器 DG ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之九（第5章 總結）

ces mark TP 生成 機器 分享 png ffffff images ? ?機器學習中的概率模型和概率密度估計方法及VAE生成式模型詳解之九（第5章 總結）