核密度估計與自適應頻寬的核密度估計

最近看論文，發現一個很不錯的概率密度估計方法。在此小記一下。
先來看看準備知識。
密度估計經常在統計學中作為一種使用有限的樣本來估計其概率密度函式的方法。
我們在研究隨機變數的過程中，隨機變數的概率密度函式的作用是描述隨機變數的特性。（概率密度函式是用來描述連續型隨機變數取值的密集程度的，舉例：某地某次考試的成績近似服從均值為80的正態分佈,即平均分是80分,由正態分佈的圖形知x=80時的函式值最大,即隨機變數在80附近取值最密集,也即考試成績在80分左右的人最多。）但是在實際應用中，總體概率密度函式通常是未知的，那麼如何來估計總體概率密度呢？一般，我們通過抽樣或者採集一定的樣本，可以根據統計學知識從樣本集合中推斷總體概率密度。這種方法統稱為概率密度估計

，即根據訓練樣本來確定隨機變數的概率分佈。一般概率密度估計方法方法大致分為兩類：引數估計和非引數估計。
引數估計(Parametric Estimation)是根據對問題的經驗知識，假設問題具有某種數學模型，隨機變數服從某種分佈，即先假定概率密度函式的形式，然後通過訓練資料估計出分佈函式的引數。常見的引數估計方法有極大似然估計方法和貝葉斯估計方法。對於引數估計，根據樣本中是否已知樣本所屬類別（即是否帶標籤）將引數估計又劃分為監督引數估計和非監督引數估計。監督引數估計是由已知類別的樣本集對總體分佈的某些引數進行統計推斷。而無監督引數估計已知總體概率密度函式形式但未知樣本所屬的類別，要求推斷出概率密度函式的某些引數，這種推斷方法稱之為非監督情況下的引數估計。
非引數估計

(Nonparametric Estimation)是在已知樣本所屬的類別不假定總體分佈形式下，基於大樣本的性質，直接利用樣本估計出整個函式。在很多情況下，我們對樣本的分佈並沒有充分的瞭解，無法事先給出密度函式的形式，而且有些樣本分佈的情況也很難用簡單的函式來描述。在這種情況下，就需要用到非引數估計。但是，並不是非引數估計一定優於引數估計，因為非引數估計受訓練樣本影響，其完備性或泛化能力不會很好；且這種估計只能用數值方法取得，無法得到完美的封閉函式圖形。常用的非引數估計方法有直方圖法，核概率密度估計等。
（若有閒暇，後續將極大似然、貝葉斯估計等等估計方法詳細總結）
這裡說說核密度估計方法（也有稱之為P

arzen窗法）
進入正題
核密度估計的形式：

f^h(x)=1n∑i=1nKh(x−xi)=1nh∑i=1nK(x−xih)
這裡K(x) 是核函式（非負，積分為1，均值為0，符合概率密度的性質），h>0是頻寬。有很多種核函式，uniform,triangular,biweight,triweight,Epanechnikov,normal等。各種核函式的圖形如下：
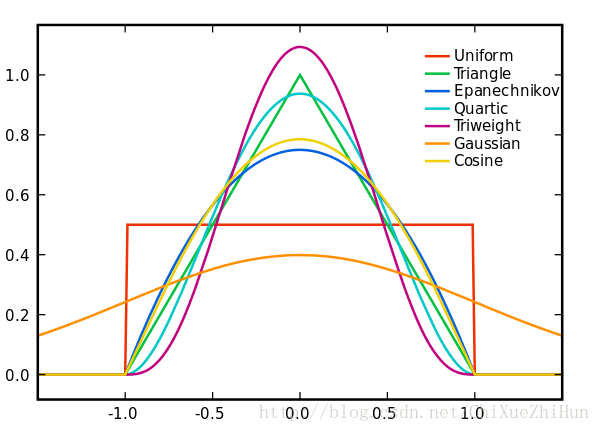
各種核函式曲線

由於高斯核心方便的數學性質，也經常使用 K(x)=ϕ(x)，ϕ(x)為標準正態概率密度函式。核密度估計與直方圖很類似，但相比於直方圖還有光滑連續的性質。
舉例理解（該例子來自維基百科https://en.wikipedia.org/wiki/Kernel_density_estimation）
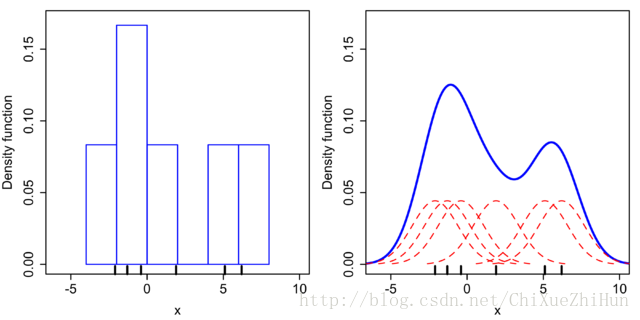
已知：6個數據點
x1=−2.1，x2=−1.3，x3=−0.4，x4=1.9，x5=5.1，x6=6.2
對於直方圖，首先將水平軸劃分為覆蓋資料範圍的子間隔或區段。在這種情況下，我們有6個寬度為2的矩形。每當資料點落在此間隔內時，我們放置一個高度為112的矩形。對於核密度估計，我們在每個資料點xi上放置方差2.25（由紅色虛線表示）的正態核函式。疊加一起得到核密度估計的結果，藍色線表示。
很明顯，直方圖得到的密度估計平滑程度比使用核密度估計得到的密度函式要差很多.
現在問題是如何選定核函式的“方差”呢？這其實是由h來決定，不同的頻寬h下的核函式估計結果差異很大。
這裡寫圖片描述

核頻寬的選擇
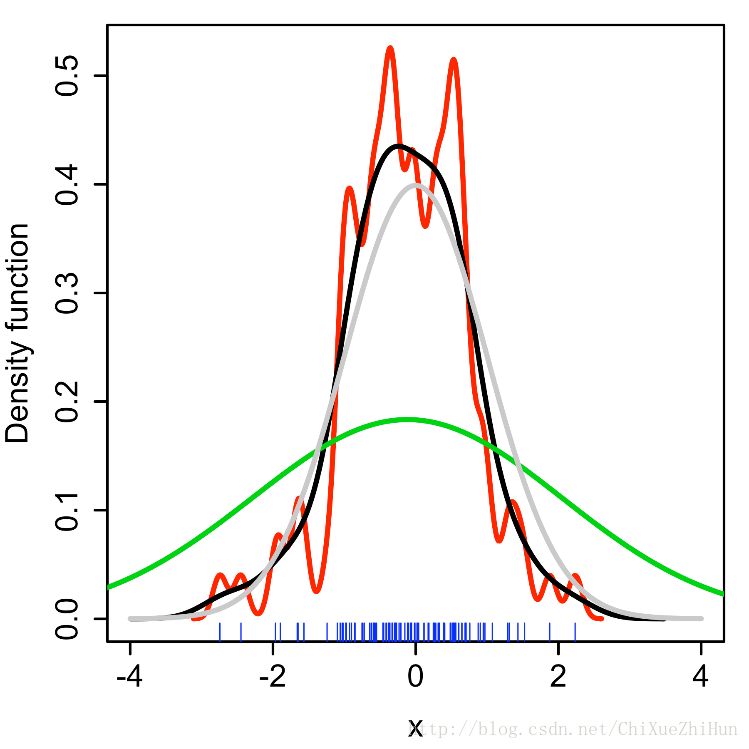
頻寬是一個自由引數，對所得到的估計值有很大的影響。為了說明效果，舉個例子：
下圖是從標準正態分佈中抽取的隨機樣本（橫軸上的藍色的點點代表樣本點）灰色曲線是真是的概率密度（正態密度，均值0，方差1）。相比之下，紅色曲線是使用了過小的頻寬h(=0.05)得出的概率密度曲線，可見其波折陡峭；綠色曲線過於平滑，因為它使用了過大的頻寬h(=2)，掩蓋了資料大部分基礎結構。

這裡寫圖片描述

那麼對於h的選擇可以使用最小化L2風險函式（即平均積分平方誤差,mean intergrated squared error）。

MISE(h)=E[∫(f^h(x)−f(x))2dx]

在weakassumptions下，MISE(h)=AMISE(h)+o(1nh+h4)，其中AMISE為漸進的MISE。而AMISE有，

AMISE(h)=R(K)nh+14m2(K)2h4R(f′′)
其中，
R(g)=∫g(x)2dx
m2(K)=∫x2K(x)dx
為了使MISE(h)最小，則轉化為求極點問題，
∂AMISE(h)∂h=−R(

核密度估計與自適應頻寬的核密度估計

核密度估計與自適應頻寬的核密度估計

web前端-移動端響應式與自適應

[ZZ] 多領域視覺數據的轉換、關聯與自適應學習

響應式與自適應的區別

CS229 Machine Learning學習筆記:Note 12(強化學習與自適應控制)

Flex佈局與自適應rpx

淺談響應式開發與自適應佈局！

互斥鎖,自旋鎖與自適應自旋鎖

unity 2D 正交攝像機下 uGUi 比例與自適應問題

【雙11背後的技術】基於深度強化學習與自適應線上學習的搜尋和推薦演算法研究

Vulkan移植GpuImage(一)高斯模糊與自適應閾值

MATLAB中自帶的核密度估計函式

LIBSVM使用與自定義核函式

順序性，一致性，原子性：現代多核體系結構與原子操作·CAS與自旋鎖·自旋鎖與併發程式設計的原語·語句原子性和程式設計邏輯的原子性·行鎖與資料庫事務原子性·binlog與資料庫同

內核模板安裝與卸載

Linux 內核中 likely 與 unlikely 的宏定義解析

CARTA：Gartner的持續自適應風險與信任評估戰略方法簡介

Linux學習筆記之內核啟動流程與模塊機制

css基礎 BFC 不與浮動元素產生交集、自適應

自適應和響應式布局的區別，em與rem

核密度估計與自適應頻寬的核密度估計

相關推薦