score.py是FCN中用於測試測試集/驗證集的，並輸出相應的畫素準確度、平均準確度、mean IU和頻率加權交併比（frequency weighted IU）四個指標的python檔案。

score.py的原始碼如下：

from __future__ import division
import caffe
import numpy as np
import os
import sys
from datetime import datetime
from PIL import Image

def fast_hist(a, b, n):
    k = (a >= 0) & (a < n)
    return np.bincount(n * a[k].astype(int) + b[k], minlength=n**2).reshape(n, n)

def compute_hist(net, save_dir, dataset, layer='score', gt='label'):
    n_cl = net.blobs[layer].channels
    if save_dir:
        os.mkdir(save_dir)
    hist = np.zeros((n_cl, n_cl))
    loss = 0
    for idx in dataset:
        net.forward()
        hist += fast_hist(net.blobs[gt].data[0, 0].flatten(),
                                net.blobs[layer].data[0].argmax(0).flatten(),
                                n_cl)

        if save_dir:
            im = Image.fromarray(net.blobs[layer].data[0].argmax(0).astype(np.uint8), mode='P')
            im.save(os.path.join(save_dir, idx + '.png'))
        # compute the loss as well
        loss += net.blobs['loss'].data.flat[0]
    return hist, loss / len(dataset)

def seg_tests(solver, save_format, dataset, layer='score', gt='label'):
    print '>>>', datetime.now(), 'Begin seg tests'
    solver.test_nets[0].share_with(solver.net)
    do_seg_tests(solver.test_nets[0], solver.iter, save_format, dataset, layer, gt)

def do_seg_tests(net, iter, save_format, dataset, layer='score', gt='label'):
    n_cl = net.blobs[layer].channels
    if save_format:
        save_format = save_format.format(iter)
    hist, loss = compute_hist(net, save_format, dataset, layer, gt)
    # mean loss
    print '>>>', datetime.now(), 'Iteration', iter, 'loss', loss
    # overall accuracy
    acc = np.diag(hist).sum() / hist.sum()
    print '>>>', datetime.now(), 'Iteration', iter, 'overall accuracy', acc
    # per-class accuracy
    acc = np.diag(hist) / hist.sum(1)
    print '>>>', datetime.now(), 'Iteration', iter, 'mean accuracy', np.nanmean(acc)
    # per-class IU
    iu = np.diag(hist) / (hist.sum(1) + hist.sum(0) - np.diag(hist))
    print '>>>', datetime.now(), 'Iteration', iter, 'mean IU', np.nanmean(iu)
    freq = hist.sum(1) / hist.sum()
    print '>>>', datetime.now(), 'Iteration', iter, 'fwavacc', \
            (freq[freq > 0] * iu[freq > 0]).sum()
    return hist
 

詳細解讀如下：

（1）fast_hist()函式

'''
產生n×n的分類統計表
引數a：標籤圖（轉換為一行輸入），即真實的標籤
引數b：score層輸出的預測圖（轉換為一行輸入），即預測的標籤
引數n:類別數
'''
def fast_hist(a, b, n):
    #k為掩膜（去除了255這些點（即標籤圖中的白色的輪廓），其中的a>=0是為了防止bincount()函數出錯）
    k = (a >= 0) & (a < n) 
    #bincount()函式用於統計陣列內每個非負整數的個數
    #詳見https://docs.scipy.org/doc/numpy/reference/generated/numpy.bincount.html
    return np.bincount(n * a[k].astype(int) + b[k], minlength=n**2).reshape(n, n)
 

此函式用於產生n*n的分類統計表，還不理解的可以看如下分析：

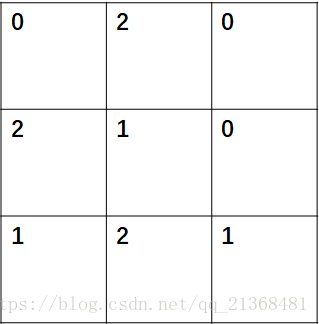
假如輸入的標籤圖a是3*3的，如下左圖，圖中的數字表示該畫素點的歸屬，即每個畫素點所屬的類別（其中n=3，即共有三種類別）；預測標籤圖b的大小和a相同，如右圖所示（圖中的數字也代表每個畫素點的類別歸屬）。

直觀上看，b中預測的標籤有兩個畫素點預測出錯，即

\[b_{01},b_{20}\]

原始碼中的這句語句是精華：np.bincount(n * a[k].astype(int) + b[k], minlength=n**2)

其作用是產生一行n*n個元素的向量，向量中的每個元素儲存統計結果，假如該向量為d，則其中的d(i*n+j)表示預測結果為類別j，實際標籤為類別i的所有畫素點的數目。

將上述的a、b和n輸入fast_hist(a, b, n)，所產生的d為：d=(3,0,0,0,2,1,0,1,2)，其中的d(1*3+1)=d(4)表示預測類別為1，實際標籤也為1的所有畫素點數目為2。

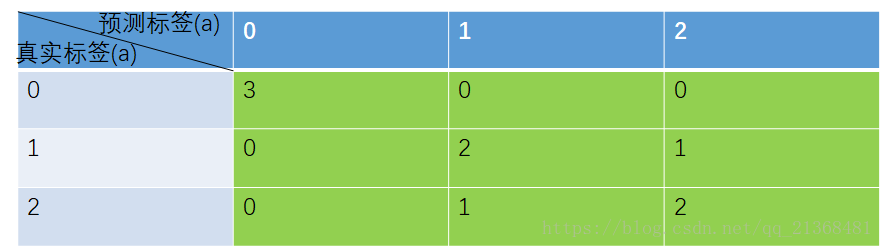
通過reshape(n, n)將向量d轉換為3*3的矩陣，其結果如下表（該矩陣即為下表中的綠色部分）：

其中綠色的3*3表格統計的含義，拿數字3所在的這一格為例，即預測標籤中被預測為類別0的且其真實標籤也為0的所有畫素點數目之和。

上述表格有幾點需要注意的是（這三條是用於計算一開始所講的四個指標的基礎）：

①綠色表格中對角線元素上的數字即為該類別預測正確的畫素點數目，非對角線元素都是預測錯誤的，拿最後一行的數字1為例，其含義即為有一個原本應屬於類別2的畫素點被錯誤地預測為類別1；

②綠色表格的每一行求和得到的數字的含義是真實標籤中屬於某一類別的所有畫素點數目，拿第一行為例，3+0+0=3，即真實屬於類別0的畫素點一共3個；

③綠色表格的每一列求和得到的數字的含義是預測為某一類別的所有畫素點數目，拿第二列為例，0+2+1=3，即預測為類別1的所有畫素點共有3個。

（2）compute_hist()函式

呼叫fast_hist()函式，遍歷測試集/驗證集中的所有樣本，統計總的分類統計表和loss。

def compute_hist(net, save_dir, dataset, layer='score', gt='label'):
    n_cl = net.blobs[layer].channels   #score層的特徵圖數目（也即類別數，例如VOC資料集，這裡就為21）
    if save_dir:
        os.mkdir(save_dir)   #建立目錄
    hist = np.zeros((n_cl, n_cl)) #建立一個n_cl×n_cl大小的零矩陣，用於儲存分類統計表
    loss = 0 #初始化損失
    #迴圈統計每一張測試/驗證圖片的預測結果，並求和儲存在hist中
    for idx in dataset:
        net.forward()
        #net.blobs[gt].data[0, 0]存放著H×W大小的標籤圖資料
        #net.blobs[layer].data[0]存放著C×H×W大小的預測圖資料（共C張），並通過argmax()獲得最終的
        #H×W大小的預測圖資料（資料範圍和標籤圖一致）（argmax本身得到的是最大值處的陣列索引號）
        #flatten()函式平鋪整個陣列為一行
        hist += fast_hist(net.blobs[gt].data[0, 0].flatten(),
                                net.blobs[layer].data[0].argmax(0).flatten(),
                                n_cl)

        if save_dir:
            #mode='P'表示產生一張單通道的彩色圖
            #（詳見http://pillow.readthedocs.io/en/3.1.x/handbook/concepts.html#concept-modes）
            im = Image.fromarray(net.blobs[layer].data[0].argmax(0).astype(np.uint8), mode='P')
            im.save(os.path.join(save_dir, idx + '.png'))
        # compute the loss as well
        loss += net.blobs['loss'].data.flat[0]  #累加每張測試圖的loss
    return hist, loss / len(dataset)

從最後一句 return hist, loss / len(dataset)也可以看出，返回的loss是總的loss除以總的樣本數。

還有比較驚喜的一點是這裡的im = Image.fromarray(net.blobs[layer].data[0].argmax(0).astype(np.uint8), mode='P')很有啟發，這句語句採用mode='P'的形式生成一張單通道的彩色圖（實際就是標籤圖），通過自行編寫的程式碼驗證，這個應該就是VOC資料集中產生標籤圖的一種方法。

程式碼如下：

import numpy as np
from PIL import Image
im = Image.open('C:/Users/Zheng Chen/Desktop/2007_000392.png')
in_ = np.array(im, dtype=np.uint8)
print in_
out = Image.fromarray(in_, mode='P')
im.save('C:/Users/Zheng Chen/Desktop/2008.png')

結果如下圖（左圖為原標籤圖，右圖為上部分程式碼生成的標籤圖，可以說是一模一樣）

（3）seg_tests()函式

此函式是score.py檔案的入口，即呼叫此函式便能完成整個測試，並輸出四個指標值，此函式的呼叫可以參見FCN中的solve.py檔案中的最後一部分。

#呼叫此函式，完成分割測試
def seg_tests(solver, save_format, dataset, layer='score', gt='label'):
    print '>>>', datetime.now(), 'Begin seg tests'
    solver.test_nets[0].share_with(solver.net)
    do_seg_tests(solver.test_nets[0], solver.iter, save_format, dataset, layer, gt)

（4）do_seg_tests()函式

此函式在compute_hist的基礎上，計算出一開始就提出的四個評價指標。

def do_seg_tests(net, iter, save_format, dataset, layer='score', gt='label'):
    n_cl = net.blobs[layer].channels  #score層的特徵圖數目（也即類別數，例如VOC資料集，這裡就為21）
    if save_format:
        save_format = save_format.format(iter)
    #呼叫compute_hist統計分割結果
    hist, loss = compute_hist(net, save_format, dataset, layer, gt) 
    # mean loss 平均loss（即所有測試集總體誤差/測試集數目）
    print '>>>', datetime.now(), 'Iteration', iter, 'loss', loss
    # overall accuracy 總體準確度（hist對角線為正確分類結果，其餘均為錯誤分類結果）
    #np.diag()詳見https://docs.scipy.org/doc/numpy/reference/generated/numpy.diag.html
    acc = np.diag(hist).sum() / hist.sum()
    print '>>>', datetime.now(), 'Iteration', iter, 'overall accuracy', acc
    # per-class accuracy 每一類的準確度
    acc = np.diag(hist) / hist.sum(1) #/為對應位相除;sum(1)為按行求和
    #輸出平均準確度（注意平均準確度與總體準確度但區別）
    #np.nanmean()詳見https://docs.scipy.org/doc/numpy/reference/generated/numpy.nanmean.html
    print '>>>', datetime.now(), 'Iteration', iter, 'mean accuracy', np.nanmean(acc) 
    # per-class IU 每一類的交併比
    #sum(0)為按列求和
    iu = np.diag(hist) / (hist.sum(1) + hist.sum(0) - np.diag(hist))
    #輸出平均交併比
    print '>>>', datetime.now(), 'Iteration', iter, 'mean IU', np.nanmean(iu)
    freq = hist.sum(1) / hist.sum()
    #輸出頻率加權交併比（frequency weighted IU）
    print '>>>', datetime.now(), 'Iteration', iter, 'fwavacc', \
            (freq[freq > 0] * iu[freq > 0]).sum()
    return hist

在此，介紹一下FCN中用到的四個評價指標（對應FCN論文中的第5部分（Results部分））。

①畫素準確度（對應原始碼解析中的overall accuracy）：

\[\sum _{i}n_{ii}/\sum _{i}t_{i}\]

②平均準確度（對應原始碼中的mean accuracy）：

\[(\frac{1}{n_{cl}})\sum _{i}n_{ii}/t_{i}\]

③mean IU（平均交併比）：

\[(\frac{1}{n_{cl}})\sum _{i}\frac{n_{ii}}{t_{i}+\sum _{j}n_{ji}-n_{ii}}\]

④頻率加權交併比（frequency weighted IU，對應原始碼中的fwavacc）：

\[(\frac{1}{\sum _{k}t_{k}})\sum _{i}\frac{t_{i}n_{ii}}{t_{i}+\sum _{j}n_{ji}-n_{ii}}\]

其中nij為第i類畫素被預測屬於第j類的數目；ncl為類別數；

\[t_{i}=\sum _{j}n_{ij}\]

表示屬於第i類的所有畫素數目

對應do_seg_tests()函式中的原始碼，相信大家肯定能更好理解和掌握這四個指標的計算技巧。

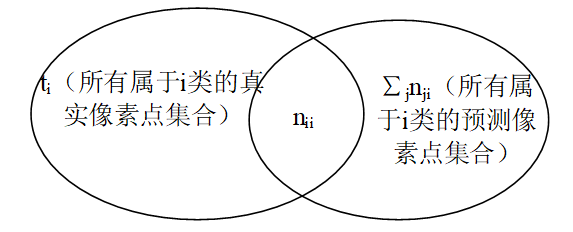
其中還有一點，就是交併比IU，為所有真實屬於第i類的畫素點所組成的集合A與所有預測屬於第i類的畫素點所組成的集合B的交集和並集之比，如下圖