本節將研究深度學習網路權值設計的重要思想之一：自編碼思想，在正式介紹之前先以一個簡單的介紹一篇，一層隱含層網路的自編碼學習問題。

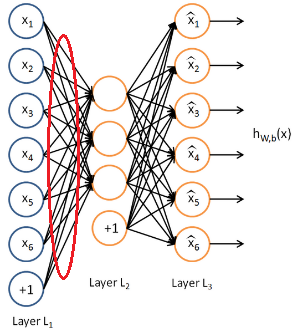
什麼是自編碼？所謂自編碼就是自己給自己編碼，再簡單點就是令輸出等於輸入自己。以一個簡單三層網路為例如下：

這裡我們假設輸出等於輸入來訓練這個網路引數（可能訓練好的網路引數不可能讓輸出百分百等於輸入，至少會非常接近吧）。那麼這個網路在輸入確定了以後（這時輸出也就確定了吧），唯一需要確定的就是隱含層的個數了吧，以上述這個圖為例，我們可以看到，網路的輸入與輸出都是一個6維的向量，而隱含層是3個，也就是3維。

那麼這種自編碼有什麼意義呢？它又有什麼用呢？可以看到，自編碼可以使得網路通過學習轉化成一組另外的量，這組量又可以通過譯碼恢復成原始的量，這樣一來一回的過程看上去沒什麼用，但是你把分開著來看就會發現很有用，原始的量可以通過編碼對映成另一組量吧，這一組量既然可以通過譯碼恢復成原始的量，說明了什麼？中間這一層的輸出是不是就是原始輸入的另外一種表達了？是的。這就好比一個人，你看得到時候直接看就是一個人，當你看不到人的時候，比如說你聽到了他的名字，你也知道這個名字表示的就是這個人。所以這個名字就是這個人的另一種條件下的新特徵，而往往這種新特徵更能去分這個人是誰。

好了再看看上面這個圖，輸入6維，隱含層以後變成了3維，輸出還是6維，我們單看到隱含層發現了什麼？是不是輸入從6維降到了3維？但是這3為在某種意義上還是原始資料的典型特徵吧，言外之意是不是相當於降維了。如果知道主成分分析法（PCA）的人應該瞭解，pca方法其實就是實現資料降維的，那麼在這裡我們通過這種自編碼，規定隱含層神經元的個數以後，通過自編碼的訓練，讓網路的輸出儘可能的等於輸入，待自編碼完成後（也就是誤差達到可接受範圍），那麼輸入通過隱含層的輸出就相當於降維了吧（前提是隱含層的神經元個數要小於輸入維數，這樣才叫降維，否則的話叫升維），說到升維，瞭解PCA的朋友你們有沒有試過PCA升維呢？PCA能不能升維呢？哈哈，貌似不能，沒試過。但是理論上是可以的。那麼升維相當於將資訊複雜化，這種操作有沒有用呢？可能還是有用的吧，瞭解SVM的朋友知道，SVM裡面就有將非線性資料通過升維以後可以線上性範圍內可分，那麼這裡的升維是不是也能將原始非線性的資料變到線性呢？可以去試試看，應該有那麼個意思。

好了說了這麼多，我們還是來看降維的情況，通過自編碼實現資料的降維思想最初是2006年深度學習領域大牛Hinton想出來的，並且發表在頂級期刊Science上，文章的出處在這裡：

該篇經典之作也被視為深度學習的開山之作，自此以後深度學習火了起來，並且逐漸打敗傳統模式識別領域的淺層學習演算法。我們知道，機器學習或者模式識別，對資料的主要工作在做什麼？無非提取資料的主要特徵，那麼以前可能所有的特徵要麼是人為設計出來，要麼是淺層學習出來的，像PCA，他們雖然一定程度上有用，但是相對於深度學習這種將資料的各個層次的特徵都學習出來了的相比自然弱了不少，這也是深度學習的最強大之處。

瞭解了自編碼，下面我們來實際看看這種自編碼的效果。
這裡以matlab平臺實驗，假設我們選取一系列小塊影象（至於小塊選多大，這裡考慮速度原因，單檯筆記本的計算原因，選擇6*6的小塊影象，其實這是很小了，所以效果不是很明顯，大概這個意思）作為輸出來進行三層網路的自編碼學習，然後看看隱含層學習到的特徵是什麼。選擇matlab是因為它自帶神經網路的建構函式便於實驗，關於其神經網路工具箱的使用介紹，看這篇

好了開始實驗吧，首先我們需要找到自編碼的輸入樣本，這裡我們以每個6*6的小塊影象作為一個樣本，先準備好很多這樣的小塊影象，假設準備1000個吧，至於怎麼準備，你可以讓每個小塊假設是從某個大影象上隨機擷取的好了。

clc
clear
%選擇塊影象的大小
patch = [6,6];
%選擇塊影象的個數
num_pic = 1000;
data = zeros(num_pic,patch(1)*patch(2));
for i = 1:20
    pic_name = [num2str(i),'.jpg'];
    I = imread(pic_name);
    I = rgb2gray(I);
    for j = 1:50
        %隨機選擇塊的位置
        choose_row = round((size(I,1) - 50)*rand);
        choose_col = round((size(I,2) - 50)*rand);
        %提取塊並存起來
        I_patch = I(choose_row+1:(choose_row+6),choose_col+1:(choose_col+6));
        data((i-1)*50+j,:) = I_patch(:);
    end
end
%歸一化到0-1
data = mapminmax(data, 0, 1);
save data.mat data        

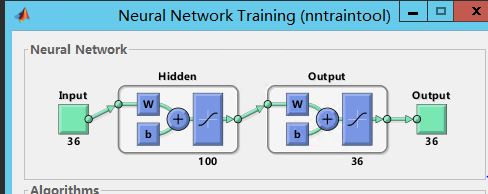
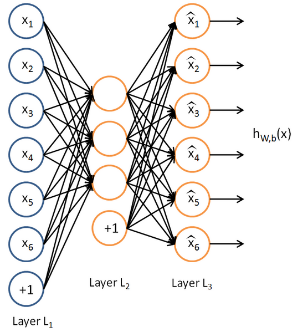
然後把這些樣本既當成輸入，也當成輸出輸送到神經網路中，比如這裡我們就得到了1000*36的樣本，每一行一個6*6的塊，1000個這樣的塊，輸出也是1000*36，就這樣。接著就可以訓練了，這裡我們再取100個隱含層。那麼假設訓練好了。我們怎麼視覺化這個結果呢？因為我們需要看的是它自編碼的編碼部分，而不是譯碼部分，所以我們只關心編碼部分的權值，像下面這個：

比如x1經過隱含層的對映會有三個輸出，那麼這三個輸出就是編碼結果，同理其他的。而我們是需要把這個對映結果顯示出來，也就是把x1對映的三個值顯示出來，同理其他的。因為這裡只有三個值，根本沒辦法視覺化。所以像上面我們取了100個隱含層，把每個輸入每個單元對映100個輸出，再把100變成10*10影象，我們就可以顯示了，並且這裡我們也只是顯示這些權值，把輸出預設為全1看看。

好了，那麼採用matlab工具箱，上述data選擇完後，構造神經網路模型，簡單的幾行程式碼：

clc
clear
load data
% data = data(1:100,:);
%% 神經網路的構建與訓練
% 構造神經網路(包含100個隱藏層的節點)
net = feedforwardnet(100);
net.layers{2}.transferFcn = 'tansig';% 輸出的對映方法，預設purelin--線性對映
% 訓練網路
net = train(net,data',data');
% 視覺化權值
show_result(net);

這樣matlab自帶它的訓練模型就出來了：

視覺化的函式也很簡單：

function show_result(net)
% 將輸入到隱含層的權值提出來並顯示
W1 = net.IW{1};
[~,n] = size(W1);
for i = 1:n
    im = W1(:,i);
    im = reshape(im,10,10);
    subplot(6,6,i);
    imshow(im,[]);
end

最終得到結果如下：

可以看到輸出的編碼樣子，有點像卻很不明顯，原因就是這是由36到100的升維，大了電腦帶不動，在matlab的這個自帶工具箱下。

所以，即使我們選擇的塊只有6*6，1000個塊，然而這個訓練過程卻很漫長，為什麼？就是matlab自帶的神經網路並不是適合這種自編碼的訓練，而是淺層的輸入到輸出的訓練，真正的自編碼訓練需要特定的設計才能保證速度，這裡只是強制使用著看看，同時自編碼還可以優化，比如加入稀疏變成稀疏自編碼等等，後面介紹一種工具箱來重新實驗這種自編碼。