題目大意：給出一個迷宮(含起點和終點)，要求找出一條路徑，這條路徑的長度必須為某個規定的長度.

在理解迷宮問題的基礎上，再做本題.本題的難點就是剪枝的問題.如果只用一般的DFS+回溯的方法求解這個問題，一定會超時，所以需要一些剪枝技巧.

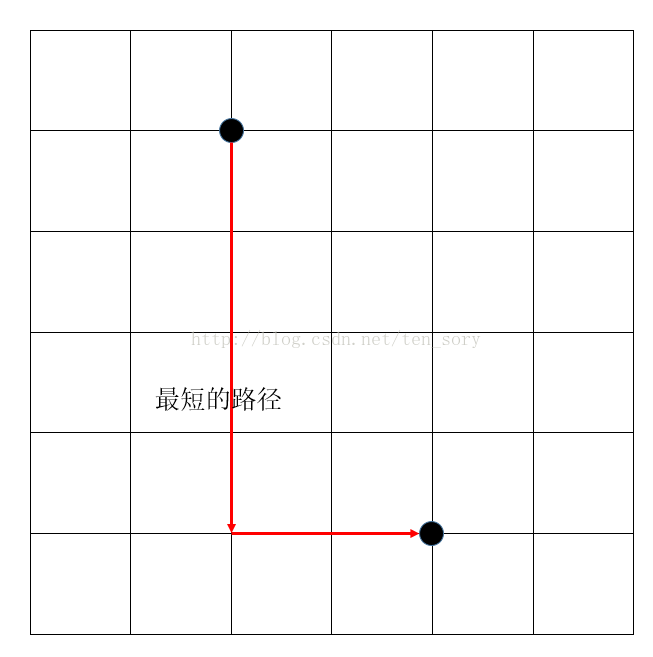
1.奇偶剪枝：如果當前位置為(x,y)，終點為(dx,dy)，要求你在T步內從(x,y)走到(dx,dy).剪枝就是確定是否存在在T步內完成(x,y)到(dx,dy)的可能性.(x,y)——>(dx,dy)的最少步驟為abs(dx-x)+abs(dy-y)，如下圖，就是兩點之間的曼哈頓距離.

當然，這個最短距離(設為path1)未必可以走得通，所以存在其他的路徑.可以肯定的是，其他任意一條路徑(設為path2)的長度一定和path1的長度的奇偶性是相同的

根據這個結論，可以得出，(x,y)到(dx,dy)的最短路徑的長度(步數)，一定和所規定的步數的奇偶性相同.如果奇偶性不同，終止這條路徑的探測.

2.小小剪枝：如果規定時間為T,而障礙物個數為wall個，則如果n*m-wall=可走的點的個數<=T，那麼一定不存在某條可行路徑的長度為T，終止即可.

程式碼如下：

#include<iostream>
using namespace std;

int flag;
char maze[10][10];
int vis[10][10];
int n,m,T,t;
int sx,sy,dx,dy;

int dir[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};//4個方向

int abs(int x){return x>0?x:(-x);}

void dfs(int x,int y,int t)
{
	if(x==dx && y==dy && t==T)//到達終點
	{
		flag = 1;
		return;
	}
	if(x<0 || x>=n || y<0 || y>=m)//出界
		return;

	/*奇偶剪枝*/
	int temp1 = abs(dx-x) + abs(dy-y);
	int temp2 = abs(T-t);//剩餘時間
	int temp = abs(temp1-temp2);
	if(temp%2!=0)
		return;

	//以當前位置(x,y)位置為起點，從上,下,左,右4個方向探測
	for(int i=0;i<4;i++)
	{
		int nx = x + dir[i][0];
		int ny = y + dir[i][1];//獲取新座標(nx,ny)

		if(0<=nx && nx<n && 0<=ny && ny<m)//(nx,ny)沒有出界
		{
			if(maze[nx][ny]!='X' && vis[nx][ny]==0)//位置(nx,ny)不是障礙，而且沒有被訪問過
			{	
				vis[nx][ny] = 1;//設定(nx,ny)為[訪問過]狀態
				dfs(nx,ny,t+1);//以(nx,ny)為起點，進行下一步探測，步數+1
				
				if(flag)	return;//*****這裡下面重點說明
				
				vis[nx][ny] = 0;//回溯
			}
		}
	}
}

int main()
{
	//freopen("in.txt","r",stdin);
	while(1)
	{
		scanf("%d%d%d",&n,&m,&T);
		if(!n && !m && !T)
			break;

		int wall=0;

		for(int i=0;i<n;i++)
		{
			cin >> maze[i];
			for(int j=0;j<m;j++)
			{
				vis[i][j] = 0;
				if(maze[i][j]=='X')    wall ++;
				else if(maze[i][j]=='S')	sx=i,sy=j,vis[i][j]=1;
				else if(maze[i][j]=='D')	dx=i,dy=j;
			}
		}

		if(n*m-wall<=T)//剪枝，可以節省一點時間
		{
			printf("NO\n");
			continue;
		}

		t = 0;
		flag = 0;
		dfs(sx,sy,t);
		if(flag)
			printf("YES\n");
		else
			printf("NO\n");
	}

	return 0;
}
 

遞迴+回溯法中，如果一個探測return了，只是本次遞迴結束了，之後回溯，進行下一次遞迴.所以某次遞迴的return不代表整個遞迴函式的return.

本題中，只要某次遞迴找到一個符合要求的路徑，就結束整個函式，而不僅僅是結束此次遞迴.

所以，本題在回溯之前，需要判斷一下是否已經找到了符合要求的路徑，即：在dfs(...)之後，立即判斷if(flag)  return;