宣告

最近在複習神經網路方面的知識。
在聽這節Andrew NG的機器學習公開課的時候，對於BP神經網路裡的錯誤反向傳播的一個公式（類似這樣的）不是特別明白。感覺和我之前看的不太一樣。就在網上找到了這篇帶樣例的文章。
為了方便分享這篇文章的實質內容，我並沒有逐字逐句地翻譯這篇文章，而是按照我覺得更易理解的方式進行的。同時，這裡面所包含的一些數學知識在這裡也沒有詳細解釋，需要大家自學。

背景

反向傳播（回饋，backpropagation）是一種訓練神經網路的常見方法。網上有大量的文章嘗試解釋反向傳播的工作原理，但卻很少有代入數值來說明的。這篇文章的作者就用了一個具體的例子來解釋反向傳播。

前言

這個教程中，作者使用了結構如下的神經網路：

它包含有兩個輸入、兩個隱藏、兩個輸出結點。其中輸入層和隱藏層都包含一個偏置結點（b1, b2）。

初始化

初始化包括兩個方面，一個是給網路中的權重矩陣初始化賦值；另一方面給一組包含輸入輸出的訓練資料。如下圖：

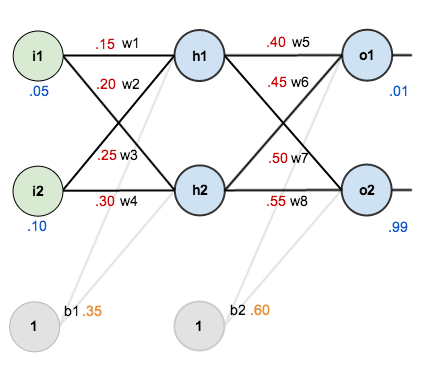
反向傳播的目的

反向傳播的目的是為了優化網路中的權重，從而將任意的輸入對映到相應的輸出。

前向傳播

1. 計算h1的輸入與權重矩陣的乘積
   
   
2. 將步驟一的結果放入啟用函式（sigmoid函式）得到h1的輸出
   
3. 重複上面的過程，我們得到h2的輸出（其輸入與權重矩陣乘積的值為：0.3925）
   
4. 由h1、h2的輸出作為輸入，計算出o1、o2的輸出。如o1的計算過程如下：
   
   
   
   同理得到o2（其輸入與權重矩陣乘積的值為：1.2249214039）
   

計算總體錯誤

作者使用了下面的公式（這個也是比較能用的公式）來計算總體錯誤：


同理：

總體錯誤為：

反向傳播

反向傳播的目的是為了更新權重引數，使得下次計算出來的結果更接近訓練樣本所提供的目標值。

更新w5、w6、w7、w8

下面以總體錯誤對w5的偏導為例。

計算偏導

通過下面這個圖來看上面的公式是怎麼來的：

1. 計算總體錯誤對o1輸出的偏導

擴充套件

作者在這裡提到了計算偏導的另外一種形式，就是Andrew NG在這節公開課裡用到的delta rule。其實是同一公式，只不過Andrew沒有在視訊裡推導公式，而是直接用了簡化的表示式，然後我就卡在這了。。。

更新權重w5

下面這個公式涉及學習率的概念(可以參考這裡）。

同理更新同一層的其它權重

注意，反向傳播的過程中，這些權重暫並不更新，整個反向傳播過程結束之後才對這個權重更新。

更新w1、w2、w3、w4

下面以w1為例。
注意，更新w1與更新w5有一些差別。

但是，

看下面的圖

也就是說，（推廣到其它多層網路）隨著反向傳播的推進，錯誤傳播的網路也在交織進行著。

下面看一下詳細過程：


其中等於


代入公式得：

同理可得：

所以，

現在計算和
因為，

同時


代入公式：


然後就可以更新w1

及w2、w3、w4。

總結一下

如果有一定的高數基礎，把上面的公式推導一下，就很容易理解了。有時間可以用python親自動手實現一下！