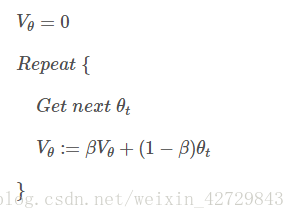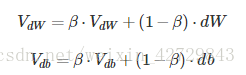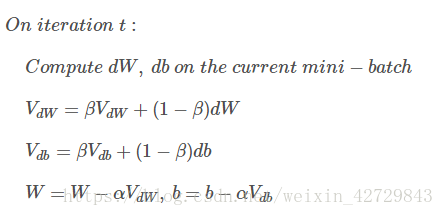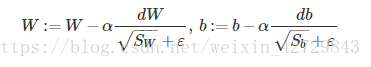目錄

1.Mini-batch gradient descent

前我們介紹的神經網路訓練過程是對所有m個樣本，稱為batch，通過向量化計算方式，同時進行的。如果m很大，例如達到百萬數量級，訓練速度往往會很慢，因為每次迭代都要對所有樣本進行進行求和運算和矩陣運算。我們將這種梯度下降演算法稱為Batch Gradient Descent。

為了解決這一問題，我們可以把m個訓練樣本分成若干個子集，稱為mini-batches，這樣每個子集包含的資料量就小了，例如只有1000，然後每次在單一子集上進行神經網路訓練，速度就會大大提高。這種梯度下降演算法叫做Mini-batch Gradient Descent。

假設總的訓練樣本個數m=5000000，其維度為(,m)。將其分成5000個子集，每個mini-batch含有1000個樣本。我們將每個mini-batch記為，其維度為(,1000)。相應的每個mini-batch的輸出記為，其維度為(1,1000)(1,1000)，且t=1,2,⋯,5000.

Mini-batches Gradient Descent的實現過程是先將總的訓練樣本分成T個子集（mini-batches），然後對每個mini-batch進行神經網路訓練，包括Forward Propagation，Compute Cost Function，Backward Propagation，迴圈至T個mini-batch都訓練完畢。

經過T次迴圈之後，所有m個訓練樣本都進行了梯度下降計算。這個過程，我們稱之為經歷了一個epoch。對於Batch Gradient Descent而言，一個epoch只進行一次梯度下降演算法；而Mini-Batches Gradient Descent，一個epoch會進行T次梯度下降演算法。

值得一提的是，對於Mini-Batches Gradient Descent，可以進行多次epoch訓練。而且，每次epoch，最好是將總體訓練資料重新打亂、重新分成T組mini-batches，這樣有利於訓練出最佳的神經網路模型。

理解Mini-batch gradient descent

Batch gradient descent和Mini-batch gradient descent的cost曲線如下圖所示：

對於一般的神經網路模型，使用Batch gradient descent，隨著迭代次數增加，cost是不斷減小的。然而，使用Mini-batch gradient descent，隨著在不同的mini-batch上迭代訓練，其cost不是單調下降，而是受類似noise的影響，出現振盪。但整體的趨勢是下降的，最終也能得到較低的cost值。

之所以出現細微振盪的原因是不同的mini-batch之間是有差異的。例如可能第一個子集(X{1},Y{1})(X{1},Y{1})是好的子集，而第二個子集(X{2},Y{2})(X{2},Y{2})包含了一些噪聲noise。出現細微振盪是正常的。

如何選擇每個mini-batch的大小，即包含的樣本個數呢？有兩個極端：如果mini-batch size=m，即為Batch gradient descent，只包含一個子集為如果mini-batch size=1，即為Stachastic gradient descent，每個樣本就是一個子集，共有m個子集。

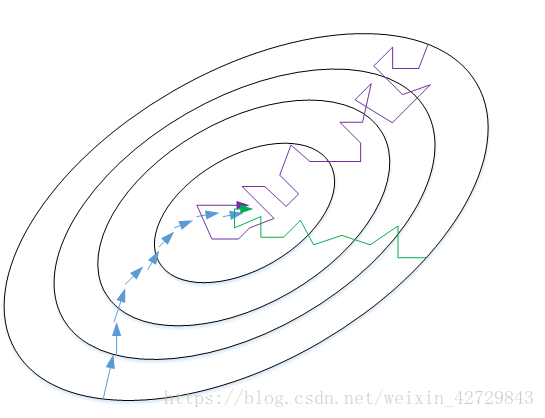
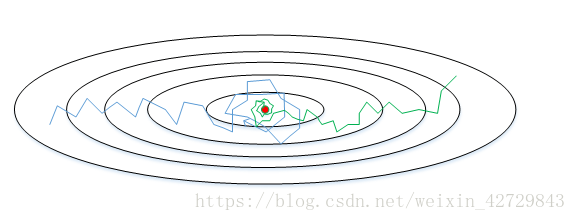
我們來比較一下Batch gradient descent和Stachastic gradient descent的梯度下降曲線。如下圖所示，藍色的線代表Batch gradient descent，紫色的線代表Stachastic gradient descent。Batch gradient descent會比較平穩地接近全域性最小值，但是因為使用了所有m個樣本，每次前進的速度有些慢。Stachastic gradient descent每次前進速度很快，但是路線曲折，有較大的振盪，最終會在最小值附近來回波動，難以真正達到最小值處。而且在數值處理上就不能使用向量化的方法來提高運算速度。

實際使用中，mini-batch size不能設定得太大（Batch gradient descent），也不能設定得太小（Stachastic gradient descent）。這樣，相當於結合了Batch gradient descent和Stachastic gradient descent各自的優點，既能使用向量化優化演算法，又能叫快速地找到最小值。mini-batch gradient descent的梯度下降曲線如下圖綠色所示，每次前進速度較快，且振盪較小，基本能接近全域性最小值。

一般來說，如果總體樣本數量m不太大時，例如m≤2000m≤2000，建議直接使用Batch gradient descent。如果總體樣本數量m很大時，建議將樣本分成許多mini-batches。推薦常用的mini-batch size為64,128,256,512。這些都是2的冪。之所以這樣設定的原因是計算機儲存資料一般是2的冪，這樣設定可以提高運算速度。

2.指數加權平均

該部分我們將介紹指數加權平均（Exponentially weighted averages）的概念。

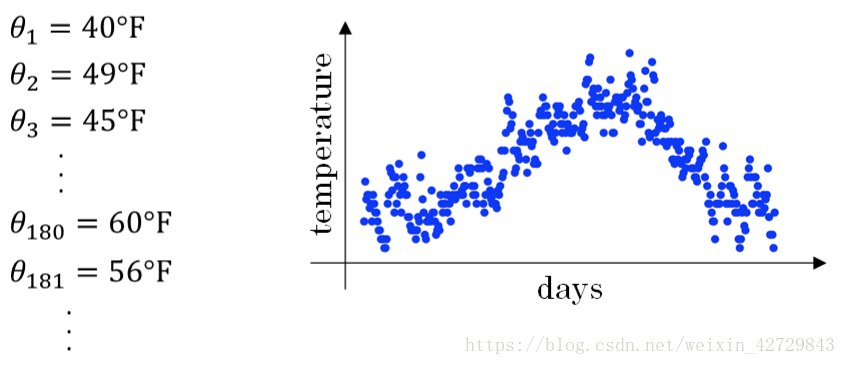
舉個例子，記錄半年內倫敦市的氣溫變化，並在二維平面上繪製出來，如下圖所示：

看上去，溫度資料似乎有noise，而且抖動較大。如果我們希望看到半年內氣溫的整體變化趨勢，可以通過區域性平均或叫移動平均（moving average）的方法來對每天氣溫進行平滑處理。

令

...

其中V表示天溫度的平均值

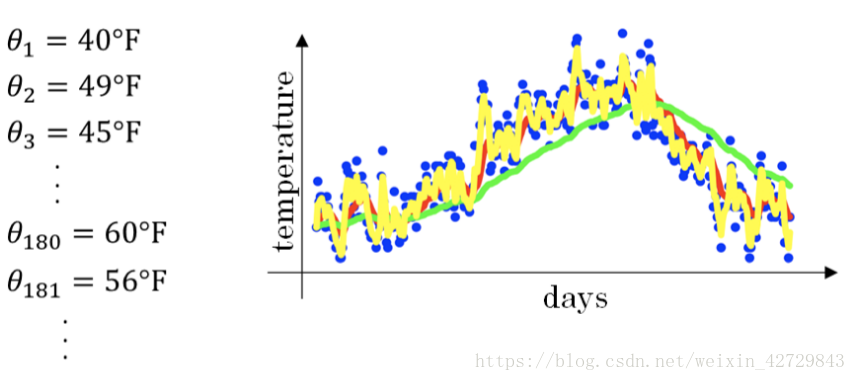
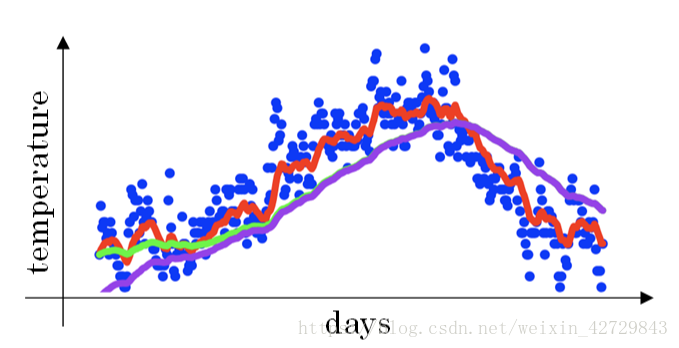
經過移動平均處理得到的氣溫如下圖紅色曲線所示：

β值越大，則指數加權平均的天數越多，平均後的趨勢線就越平緩，但是同時也會向右平移。下圖綠色曲線和黃色曲線分別表示了β=0.98和β=0.5時，指數加權平均的結果。

我們將指數加權平均公式的一般形式寫下來：

因為的次方差不多衰減到可以忽略不計，因此可以看做天溫度的指數加權平均值。

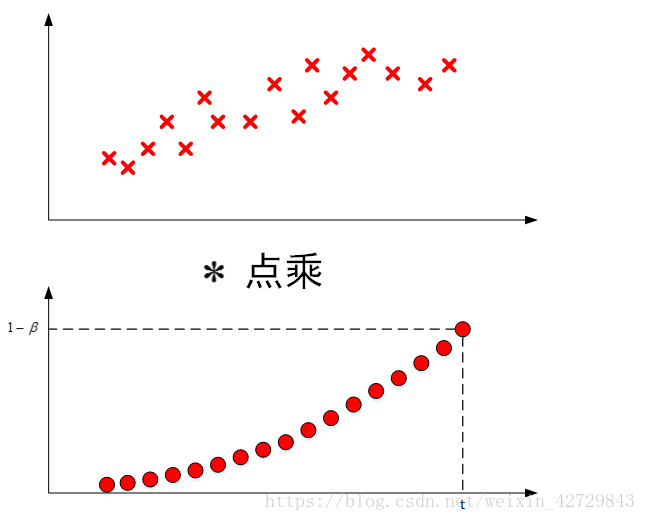
是將原始資料值與衰減指數（衰減指數相加大概約等於1）點乘，相當於做了指數衰減，離得越近，影響越大，離得越遠，影響越小，衰減越厲害。

程式碼實現如下：

指數加權平均數不是最精確的計算平均數的方法，但是其優點是佔用記憶體少，效率高，程式碼執行簡單。

指數加權平均的偏差修正

上文中提到當β=0.98時，指數加權平均結果如下圖綠色曲線所示。但是實際上，真實曲線如紫色曲線所示。

我們注意到，紫色曲線與綠色曲線的區別是，紫色曲線開始的時候相對較低一些。這是因為開始時我們設定，所以初始值會相對小一些，直到後面受前面的影響漸漸變小，趨於正常。

修正這種問題的方法是進行偏移校正（bias correction），即在每次計算完Vt後，對Vt進行下式處理：

在剛開始的時候，t比較小，(1−)<1，這樣就將VtVt修正得更大一些，效果是把紫色曲線開始部分向上提升一些，與綠色曲線接近重合。隨著 t 增大，(1−)≈1，Vt基本不變，紫色曲線與綠色曲線依然重合。這樣就實現了簡單的偏移校正，得到我們希望的綠色曲線。

值得一提的是，機器學習中，偏移校正並不是必須的。因為，在迭代一次次數後（t較大），Vt受初始值影響微乎其微，紫色曲線與綠色曲線基本重合。所以，一般可以忽略初始迭代過程，等到一定迭代之後再取值，這樣就不需要進行偏移校正了。

3.動量梯度下降法

該部分將介紹動量梯度下降演算法，其速度要比傳統的梯度下降演算法快很多。做法是在每次訓練時，對梯度進行指數加權平均處理，然後用得到的梯度值更新權重W和常數項b。下面介紹具體的實現過程。

原始的梯度下降演算法如上圖藍色折線所示。在梯度下降過程中，梯度下降的振盪較大，尤其對於W、b之間數值範圍差別較大的情況。此時每一點處的梯度只與當前方向有關，產生類似折線的效果，前進緩慢。而如果對梯度進行指數加權平均，這樣使當前梯度不僅與當前方向有關，還與之前的方向有關，這樣處理讓梯度前進方向更加平滑，減少振盪，能夠更快地到達最小值處。

權重W和常數項b的指數加權平均表示式如下：

從動量的角度來看，以權重W為例，可以成速度V，dW可以看成是加速度a。指數加權平均實際上是計算當前的速度，當前速度由之前的速度和現在的加速度共同影響。而β<1，又能限制速度過大。也就是說，當前的速度是漸變的，而不是瞬變的，是動量的過程。這保證了梯度下降的平穩性和準確性，減少振盪，較快地達到最小值處。

動量梯度下降演算法的過程如下：

初始時，令=0,=0。一般設定β=0.9，即指數加權平均前10天的資料，實際應用效果較好。

另外，關於偏移校正，可以不使用。因為經過10次迭代後，隨著滑動平均的過程，偏移情況會逐漸消失。

4.RMSprop

RMSprop是另外一種優化梯度下降速度的演算法。每次迭代訓練過程中，其權重W和常數項b的更新表示式為：

下面簡單解釋一下RMSprop演算法的原理，仍然以下圖為例，為了便於分析，令水平方向為W的方向，垂直方向為b的方向（實際上水平方向可能是W1，W2，W17的合集，垂直方向可能是W3，W4）。

從圖中可以看出，梯度下降（藍色折線）在垂直方向（b）上振盪較大，在水平方向（W）上振盪較小，表示在b方向上梯度較大，即db較大，而在W方向上梯度較小，即dW較小。因此為了加快W方向的速度減小b方向的速度減小震盪，要讓小，讓大。所以讓加上dW的平方讓加上db的平方，即加快了W方向的速度，減小了b方向的速度，減小振盪，實現快速梯度下降演算法，其梯度下降過程如綠色折線所示。總得來說，就是如果哪個方向振盪大，就減小該方向的更新速度，從而減小振盪。

還有一點需要注意的是為了避免RMSprop演算法中分母為零，通常可以在分母增加一個極小的常數ε：

其中，ε=，或者其它較小值。

5.Adam優化演算法

6.學習率衰減

減小學習因子αα也能有效提高神經網路訓練速度，這種方法被稱為learning rate decay。

Learning rate decay就是隨著迭代次數增加，學習因子αα逐漸減小。下面用圖示的方式來解釋這樣做的好處。下圖中，藍色折線表示使用恆定的學習因子α，由於每次訓練α相同，步進長度不變，在接近最優值處的振盪也大，在最優值附近較大範圍內振盪，與最優值距離就比較遠。綠色折線表示使用不斷減小的α，隨著訓練次數增加，α逐漸減小，步進長度減小，使得能夠在最優值處較小範圍內微弱振盪，不斷逼近最優值。相比較恆定的α來說，learning rate decay更接近最優值。

Learning rate decay中對αα可由下列公式得到：

其中，deacy_rate是引數（可調），epoch是訓練完所有樣本的次數。隨著epoch增加，α會不斷變小。

除了上面計算α的公式之外，還有其它可供選擇的計算公式：

其中，k為可調引數，t為mini-bach number。

除此之外，還可以設定α為關於 t 的離散值，隨著 t 增加，α呈階梯式減小。當然，也可以根據訓練情況靈活調整當前的α值，但會比較耗時間。

7.區域性最優問題

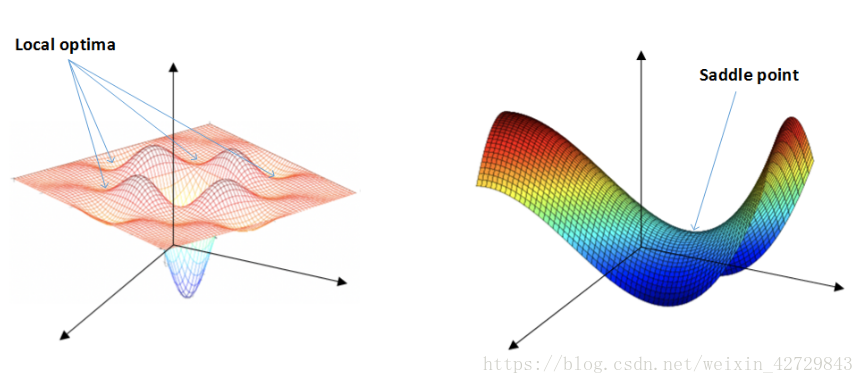
在使用梯度下降演算法不斷減小cost function時，可能會得到區域性最優解（local optima）而不是全域性最優解（global optima）。之前我們對區域性最優解的理解是形如碗狀的凹槽，如下圖左邊所示。但是在神經網路中，local optima的概念發生了變化。在高維空間的代價函式（如有20000個引數）中，梯度為0的點是區域性最優點（所有維都是凹的）的概率是很小的，更有可能的是梯度為0的點是鞍點（部分維是凹的，部分維是凸的）。

類似馬鞍狀的plateaus會降低神經網路學習速度。Plateaus是梯度接近於零的平緩區域，如下圖所示。在plateaus上梯度很小，前進緩慢，到達saddle point需要很長時間。到達saddle point後，由於隨機擾動，梯度一般能夠沿著圖中綠色箭頭，離開saddle point，繼續前進，只是在plateaus上花費了太多時間。

總的來說，關於local optima，有兩點總結：

• （只要選擇合理的強大的神經網路）一般不太可能陷入這種壞的“local optima”（如上圖路線）

• Plateaus可能會使梯度下降變慢，降低學習速度

值得一提的是，上文介紹的動量梯度下降，RMSprop，Adam演算法都能有效解決plateaus下降過慢的問題，大大提高神經網路的學習速度。