全面理解卷積
文末有很多經典文章供參考。
非常推薦這一篇文章:談談離散卷積和卷積神經網路
概述
- 卷積的實質:
- 數學角度:==卷積實際上是一種積分運算,而且是線性運算(從離散角度理解),用來求兩個曲線重疊區域的面積,可以看作加權求和。==,實際上積分就是極限求和。所以離散和連續並沒有本質區別。
- 訊號角度:對訊號進行濾波
卷積定理可以將時空域的卷積等價位頻域的相乘,進而利用FFT等快速演算法,可以節約很大的運算成本
卷積分為:
* 連續卷積
* 離散卷積
注:二者的區別實際上就是連續和離散的區別, 我們課本上學的一般是聯絡形式,但是為了推廣到高維,所以之後我們會採用離散的形式去表示
來源

從衝激函式而來,為了表示某一個瞬時量,要對這個瞬時量求積分(面積),圖1-8有一個箭頭就是為了說明無論這個矩形脈衝訊號,被擠壓的如何小,都始終存在。
卷積的數學表示:
- 一維情況下的卷積
- 連續卷積
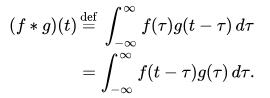
- 離散化表示
注: k是參變數, i是自變數,這裡h就是一維的卷積核。
- 多維卷積(以二維為例)
注: p,q是參變數,i,j是自變數,這裡h就是二維的卷積核。
卷積數學細節的注意點
- 卷積核實際上就是滑動的那個mask(掩模/模板),也就是對應公式(1),(2)的h。大多數的mask是對稱的,詳情戳這裡
一維卷積後的長度是原來兩個序列長度求和減1(因為最大長度要使得兩個序列至少有1個項重合,即兩個序列長度求和再減去重合的一項的長度)
公式(1),(2)中的序號k,q,p其實表示的是兩個卷積序列的相對位置關係,也就是與被卷積訊號的座標不相同。
卷積的兩個訊號的座標既可以是時間座標也可以是空間的座標,甚至是時空座標。只不過,如果是時間座標,注意座標不可為負。
連續卷積動圖演示

注: 這個圖在訊號分析的計算中是有一個結論的,完全相同的兩個矩形波疊加會產生一個三角波,不相同的矩形波會產生一個梯形波。所以在計算三角波和矩形波的頻域表示的時候,常常會用到這個結論。
==詳細推導,之後補上==

3. 理解本質去計算:
卷積在影象處理的應用
首先宣告影象對於計算機來說就是數值矩陣
- 灰度圖就是一個數值矩陣
- 彩色圖就是多個數值矩陣的疊加。
卷積在影象中的應用
1. 用來消除噪聲
2. 特徵增強
原因:
在概述中我們提到:==卷積實際上是一種積分運算,用來求兩個曲線重疊區域的面積,可以看作加權求和。
濾波器角度理解:積分運算本來就有平滑的作用(因為是累積的呀,略略略),所以比起卷積前的兩個函式,兩者卷積後函式會變得更加光滑,相當於一個高通濾波器(高於截至頻率頻的訊號可以通過,低於截止頻率的訊號不可以通過。),所以高頻的噪聲受到卷積的影響更大,也就是頻率越高,收到卷積的影響就越到,就會變得相對自己越平滑,所以就可以有效的濾波。而噪聲一般都是高頻訊號。
加權求和理解: 每一點的畫素值都是周圍點的畫素值的加權平均代替。


