關於回溯法和DFS做下總結:
在程式設計中有一類題目求一組解或者求全部解或者求最優解等系列問題,不是根據某種特定的規則來計算,而是通過試探和回溯的搜尋來查詢結果,通常都會設計為遞迴形式.

這類題本身是一顆狀態樹,當只有兩種情況的時候則為二叉樹,這棵樹不是之前建立的,而是隱含在遍歷過程中的.接下來根據一些題目來提高認識.

一.二叉狀態樹

題目:

說白了就是一個全遍歷的過程,找出每一種可能的組合.對於123則有題目中的8種情況.

思路:
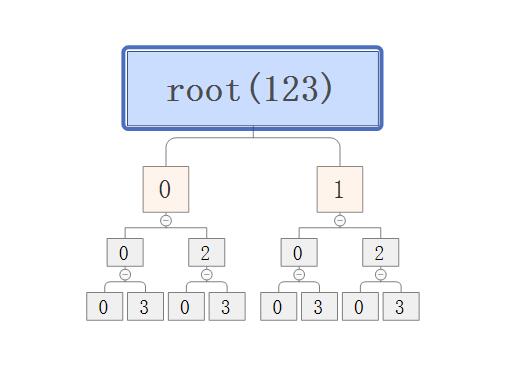
這樣的全排列問題可以從元素本身入手,每一個元素只有兩種狀態,被選擇和不被選擇,那麼就可以用一顆二叉樹來表示
0表示未選擇

那麼遞迴程式就可以設計如下

public class Test10 {

    static String str = "";
    public static void main(String[] args) {
        int[] A = {1,2,3};
        DFS(A, 0);
    }
    /**
     * @param a 存放要遍歷的集合
     * @param n 代表當前選擇第n個元素
     */
    private static void DFS(int[] a,int n){
        if (n >= a.length) {
            if
 
 (str.isEmpty()) {
                System.out.println("$");//集合為空的話設定為$符號
            }else {
                System.out.println(str);
            }
        }else {
            //不選擇當前值
            DFS(a, n+1);
            //選擇當前值
            String strTemp = new String(str);//新建一個變數,為了回溯時可以退回到之前的資料
            str = str+a[n];
            DFS(a, n+1
 
);
            str = strTemp;//回溯到之前的str狀態
        }
    }
}

二.四皇后問題(可擴充套件為n皇后)

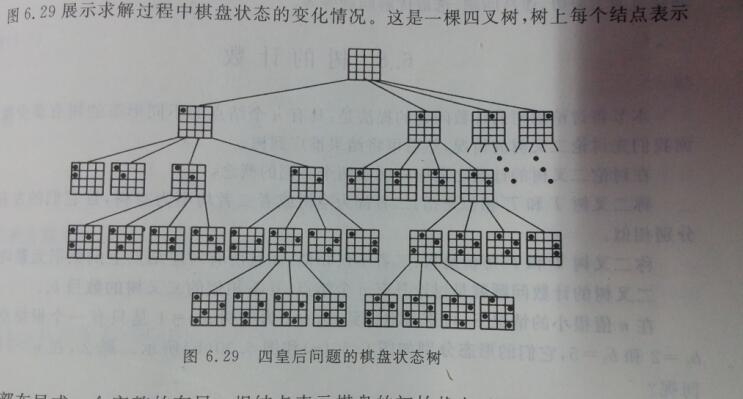
四皇后如果用回溯法的話,會先生一個四叉樹,和字典樹比較類似了,如下圖

可以看出來和上面一樣的情況,對於四皇后,每一次選擇都有四种放置棋子的方式,所以只要一個一個放置就可以找出全部可以放置的結果了.
對於有重複的,直接截枝,也就是沒必要再往下尋找了

對於n皇后,把陣列中的4改為n的值就好了

import java.util.Arrays;

public class Test11 {

    private static int A[] = new int[4+1];//四皇后是4*4的格子,為了便於觀看,0處不要

    private static int count = 0;

    public static void main(String[] args) {
        DFS(1);
        System.out.println(count);
    }

    /**
     * @param n 表示要放置的行數
     */
    private static void DFS(int n){
        if (n >= A.length) {
            count++;
            printArr();
        }else {
            //對於每一個行,棋子都有四种放置狀態
            for (int j = 1; j < A.length; j++) {
                if (check(n, j)) {//如果可以放置
                    A[n] = j;//放置棋子
                    DFS(n+1);//放置下一行
                }
                A[n] = 0;//回溯時,拿掉棋子
            }
        }

    }
    //列印陣列
    private static void printArr(){
            System.out.println(Arrays.toString(A));
        System.out.println("-------------------------------------");
    }
    /*
     *檢測是否符合條件
     *j==A[i] 檢測當前列上有沒有棋子
     *Math.abs(n-i) == Math.abs(j - A[i] 檢測斜線上有沒有棋子
     */
    private static boolean check(int n,int j){
        for (int i = 1; i < n; i++) {
            if (j==A[i] || Math.abs(n-i) == Math.abs(j - A[i])) {
                return false;
            }
        }
        return true;
    }
}

三.poj1416

題目:
現在你要研發一種新型的碎紙機，待粉碎的紙上面有一串數字，要求把紙粉碎成的幾片上的數字的和儘量接近而不能超過給定的數字target number。比如：一片紙上的數字為12346，target number為50，那麼就可以把紙粉碎為1、2、34、6，其加和為43，是所有粉碎方法中最接近50而不超過50的最優解。

解釋:
題目換句話來理解就是有一串數字中間用+號來連線,使其結果小於或等於指定值的最優解.

EG:

題目 50 12346

那麼可以分為以下幾種情況
50 1+2+3+4+6=16

50 12+3+4+6=25

50 123+4+6=133

50 1+23+4+6=34

這道題就可以利用第一題二叉狀態樹想法來考慮,對於數字之間的空,可以選擇插入+號和不插入加號

public class Test12 {

    private static int A[] = {1,2,3,4,6};

    private static int total = 50;
    private static int max = 0;
    private static String maxStr = null;
    private static StringBuilder builder = new StringBuilder();

    public static void main(String[] args) {
        DFS(0, "");
        System.out.println(max);
        System.out.println(maxStr);
    }

    private static void DFS(int n,String sum){
        if (n == A.length) {
            int sumtemp = getSum(sum);
            if (sumtemp <= total) {
                if (sumtemp > max) {
                    max = sumtemp;//儲存最大值
                    maxStr = sum;//儲存最大值對應的串
                }
            }
        }else {
            if (getSum(sum+A[n]) <= total) {//剪枝操作
                DFS(n+1,sum+A[n]);//不加+號
            }
            if (getSum(sum + "+" + A[n]) <= total) {
                DFS(n+1, sum + "+" + A[n]);//加+號
            }
        }
    }
    /**
     * 根據字串計算出其數值大小
     * @param str
     * @return
     */
    private static int getSum(String str){
        String[] arr = str.split("\\+");//不能直接寫+號,需要轉義下
        int sum = 0;
        for (String temp : arr) {
            if (temp != null && !"".equals(temp)) {
                sum = sum + Integer.parseInt(temp);
            }
        }
        return sum;
    }

}

這種思路和之前的思路相比,遞迴層次明顯深了,所以遞迴次數也會增多,但是 好理解,寫的迅速

四.素數環

要點1,因為是環,且要從1開始排列,所以第一個元素只能是1,其他不是1的,一定是重複的
要點2,高效判斷一個數是素數,運用素數mod6的關係
要點3,元素不能重複,因此回溯的時候要回溯標誌量

import java.util.Arrays;

public class Test21 {
    static int n = 6;
    static int[] visit = new int[n+1];
    static int[] order = new int[n+1];
    public static void main(String[] args) {
        order[1] = 1;
        visit[1] = 1;
        DFS(2);
    }

    private static void DFS(int cur){
        //遞迴邊界,不要忘記判斷第一個和最後一個是否是素數
        if (cur == n+1 && isPrime(order[1]+order[n])) {
            System.out.println(Arrays.toString(order));
        }else {
            for (int i = 2; i <= n; i++) {
                if (visit[i] == 0) {//代表該元素沒被放置過
                    if (isPrime(order[cur-1]+i)) {//如果相鄰的是素數
                        order[cur] = i;//放置
                        visit[i] = 1;//用過
                        DFS(cur+1);
                        visit[i] = 0;//回溯
                    }
                }
            }

        }
    }
    /**
     * 判斷一個數是否為素數
     * @param num
     * @return
     */
    private static boolean isPrime(int num){
        if (num == 2 || num == 3) {
            return true;
        }
        if (num%6 !=1 && num%6 != 5) {
            return false;
        }
        for (int i = 5; i*i <= num; i=i+6) {
            if (num%i==0 || num%(i+2)==0) {
                return false;
            }
        }
        return true;
    }
}

5.困難的串

要點: 對困難串的判斷,可以採取八皇后的那種思路,不需要全部判斷,只需要判斷一部分
要點: 遞迴過程大於7就要結束遞迴,這個判斷也不知道為什麼,只能多判斷幾次,雖然做出來了,但是感覺有點暈暈的

public class Test22 {
    //計數
    private static int count = 0;
    private static int k = 30;//要求的數量
    //存放26個字母
    private static char[] arr = {'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};
    public static void main(String[] args) {
        DFS("", 3);
    }


    private static void DFS(String str,int n){
            //開始迴圈
            for (int i = 0; i < n; i++) {
                //如果是困難串則輸出
                if (isDifficultStr(str+arr[i])) {
                    //如果大於7個了,就沒必要判斷
                    if (count > k) {
                        break;
                    }
                    //儲存當前狀態,回溯用的
                    String temp = new String(str);
                    str += arr[i];
                    count++;//找到數量加1
                    //少於7個,則dfs遞迴
                    if (count < k) {
                        DFS(str, n);
                        str = temp;
                    }else if(count == k){
                        //輸出指定位置的串
                        System.out.println(str+"---"+count);
                    }

                }
        }
    }
    /**
     * 判斷是否為困難的串
     * 此方法只針對本題有效,因為本題從頭開始構造,所以前面的肯定是困難串,只有最後新增的才會影響判斷結果
     * 因為 ABAACB 類似這樣的情景不可能在判斷中出現,所以這個演算法才會成立
     * @param str
     * @return
     */
    private static boolean isDifficultStr(String str){
        boolean ischeck = true;
        for (int i = 1; 2*i <= str.length(); i++) {//i表示重複串大小
            boolean temp = true;
            for (int j = 0; j < i; j++) {
                //每次從最後一個掃描
                if (str.charAt(str.length()-j-1) != str.charAt(str.length()-i-j-1)) {
                    temp = false;//如果不等,則證明重複串不存在
                    break;
                }
            }
            if (temp) {//如果temp為true,則證明假定重複串存在,也就不是困難的串
                ischeck = false;
            }
        }

        return ischeck;
    }
}

6.方格填數

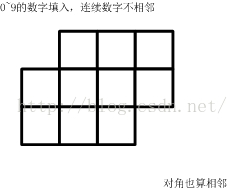
填入0~9的數字。要求：連續的兩個數字不能相鄰。（左右、上下、對角都算相鄰）一共有多少種可能的填數方案？

這道題和八皇后比較像,不過不同之處在於,八皇后每一行只填一個數,所以可以用一位陣列A[I]=j表示第i行第j列,
但是這個題目就需要每個都填寫,所以只能用二維陣列儲存
還需要注意的就是在陣列中填入數字後,回溯的時候要清理掉,因為每個格子之間有約束條件,所以才需要清理的

import java.lang.reflect.Array;
import java.util.Arrays;

public class Test3 {

    private static int[][] A = new int[3+2][4+2];

    private static int[] visit = new int[10];

    private static int count = 0;

    public static void main(String[] args) {
        for (int i = 0; i < A.length; i++) {
            Arrays.fill(A[i], -10);
        }
        DFS(1, 2);//從第一二開始遞迴
        System.out.println(count);
    }

    private static void DFS(int dep,int pos){
        if (dep == 3 && pos == 4) {
            count++;
            return;
        }
        if(pos <= 4){
            //每一個格子有10中可能性
            for (int i = 0; i < 10; i++) {
                if (check(dep, pos,i) && visit[i] == 0) {
                    A[dep][pos] = i;
                    visit[i] = 1;
                    //放置下一個
                    DFS(dep, pos+1);
                    A[dep][pos] = -10;//修改回來,不然會影響後面的計算
                    visit[i] = 0;//回溯,修改回來
                }
            }
        }else {
            //遞迴下一行
            DFS(dep+1, 1);
        }
    }

    private static boolean check(int dep,int pos,int i){
        if (Math.abs(i - A[dep+1][pos]) ==1  
            || Math.abs(i - A[dep-1][pos]) ==1  
            || Math.abs(i - A[dep][pos+1]) ==1  
            || Math.abs(i - A[dep][pos-1]) ==1  
            || Math.abs(i - A[dep+1][pos-1]) ==1  
            || Math.abs(i - A[dep+1][pos+1]) ==1  
            || Math.abs(i - A[dep-1][pos-1]) ==1  
            || Math.abs(i - A[dep-1][pos+1]) ==1  
                ) {
            return false;
        }
        return true;
    }
}