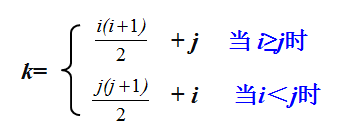coding A&D:特殊矩陣的壓縮儲存
特殊矩陣包含:
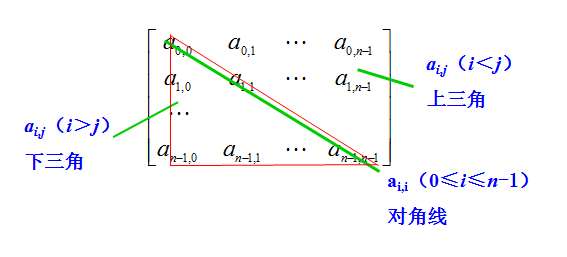
對稱矩陣:a(i,j) = a(j,i)
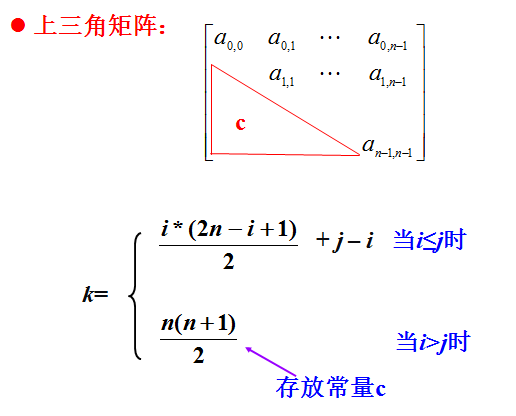
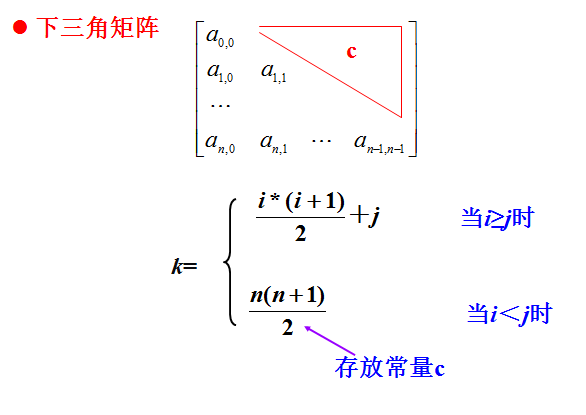
上三角矩陣/ 下三角矩陣:下三角元素均為常數的矩陣/ 下三角元素均為常數的矩陣
對角矩陣:所有非零元素集中在主對角線兩側的帶狀區域內。
稀疏矩陣:
#對稱矩陣(n階矩陣)
1.若,下標從0開始:
ai,j = aj,i
i>=0, j<= n-1
i<j:上三角區元素
i>=j:下三角區元素+主對角線元素
2.若下標從1開始:
i>=1, j <= n
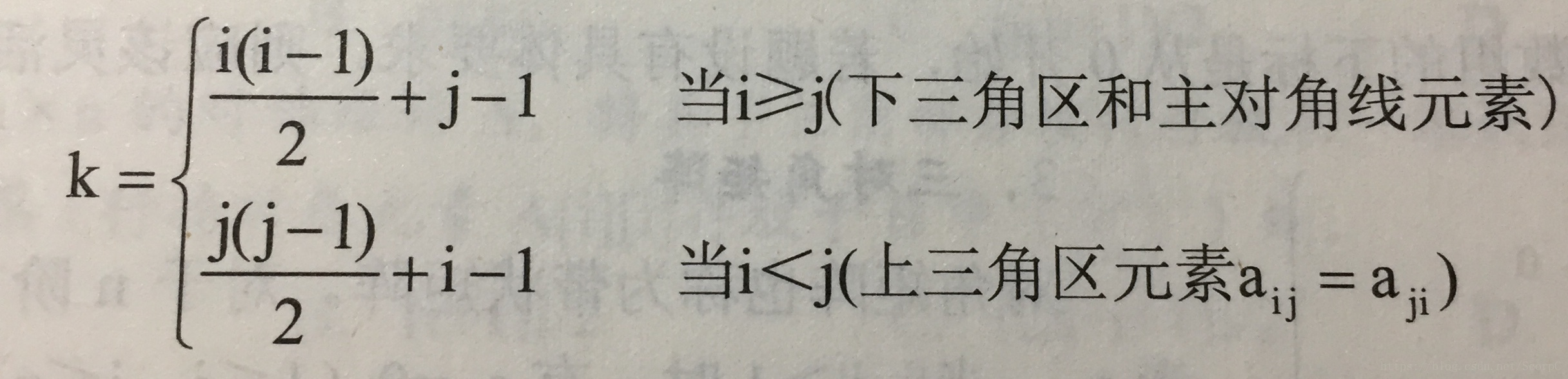
#三角矩陣
跟對稱矩陣儲存相似,只是一位陣列s的最後一位用來儲存常數項。
若,下標從0開始:
若,下標從1開始:
對角矩陣:
若,下標從0開始:
k = 2i + j
若,下標從1開始:
k = 2i + j - 3
#稀疏矩陣:
用三元組順序表來儲存:
相關推薦
coding A&D:特殊矩陣的壓縮儲存
特殊矩陣包含: 對稱矩陣:a(i,j) = a(j,i) 上三角矩陣/ 下三角矩陣:下三角元素均為常數的矩陣/ 下三角元素均為常數的矩陣 對角矩陣:所有非零元素集中在主對角線兩側的帶狀區域內。 稀疏矩陣: #對稱矩陣(n階矩陣) 1.若,下標從0開始: ai
coding A&D:關鍵路徑(AOE網)
1、AOE-網介紹 我們在學習拓撲排序(如果沒學,可以看看這篇部落格:拓撲排序詳解)的時候,已經接觸了什麼是AOV-網,AOV-網是優先考慮頂點的思路,而我們也同樣可以優先考慮邊,這個就是AOE-網的思路。 若在帶權的有向無環圖中,以頂點表示事件,以有向邊表示活
coding A&D:(選擇排序)堆排序
【概念】: 堆是具有以下性質的完全二叉樹: 每個結點的值都大於或等於其左右孩子結點的值,稱為大根堆; 或者每個結點的值都小於或等於其左右孩子結點的值,稱為小根堆。 (注意:這種結構是對父節點-左/右孩子節點之間做的約束,而對左-右孩子節點之間並沒有什麼
coding A&D:KMP演算法
一些演算法、資料結構長時間不用,就忘記了,甚至連概念都忘了,最麻煩的是忘記當初如何理解該概念的方法了。。。 瀏覽部落格時發現這兩位博主的博文有助於我重新理解kmp演算法,遂參考一下,進行總結,有助於以後使用: 總結如下: 【概念】:首先KMP是用來進行串的模
coding A&D:計算雜湊表
例題(來源:2010年全國統考專業課408 第一題) 一. 雜湊表—線性探測法的ASL成功、不成功計算 將關鍵字序列(7、8、30、11、18、9、14)雜湊儲存到散列表中。散列表的儲存空間是一個下標從0開始的一維陣列。雜湊函式為: H(key) = (keyx3) MOD
coding A&D:圖:最小生成樹(二):破圈法
求MST的演算法中,prim演算法和kruskal演算法思想是:“加邊”; 破圈法正好相反,破圈即為:“減邊”。 破圈法是一種貪心演算法,思想大體如下: 1.找到圖中的一個圈; 2.刪除其中的權最大的邊; 3.重複上述操作,直到圖中已無圈。 以下為bd百科中的
coding A&D:最短路徑
最短路徑問題分為兩大類: #無勸圖的單源最短路徑; #帶權有向圖的單源最短路徑、各頂點之間的最短路徑。 求解最短路徑的演算法,通常都依賴於一種性質,也就是兩點之間的最短路徑也包含了路徑上其他頂點間的最短路徑 【1】無權圖的單源最短路徑: 可用BFS廣度優先搜尋;
coding A&D:AVL平衡二叉樹的旋轉(插入結點)
【1】AVL平衡二叉樹的基本概念: 平衡二叉樹建立在二叉排序樹的基礎上,目的是使二叉排序樹的平均查詢長度更小,即讓各結點的深度儘可能小,因此,樹中每個結點的兩棵子樹的深度不要偏差太大。 平衡二叉樹的遞迴定義:平衡二叉樹是一棵二叉樹,其可以為空,或滿足如下2個性質:①左右子
coding A&D:森林與二叉樹的轉換
首先,樹轉二叉樹: 「1」兄弟+橫線 樹中的每一個結點,如果該結點有兄弟結點,那麼就在這幾個兄弟結點之間進行連線。 「2」儲存長子線 對於樹中的每一個結點,如果其有多個子節點,儲存其第一個子節點的連線,去除其他子節點的連線。 「3」調整位置 對每個結點
機器學習中的矩陣方法(附錄A): 病態矩陣與條件數
1. 病態系統 現在有線性系統: Ax = b, 解方程 很容易得到解為: x1 = -100, x2 = -200. 如果在樣本採集時存在一個微小的誤差,比如,將 A 矩陣的係數 400 改變成 401: 則得到一個截然不同的解: x1 = 40000, x2 = 79800. 當解集
稀疏矩陣-壓縮儲存-列轉置法- 一次定位快速轉置法
稀疏矩陣的壓縮儲存壓縮儲存值儲存極少數的有效資料。使用{row,col,value}三元組儲存每一個有效資料,三元組按原矩陣中的位置,以行優先順序先後順序依次存放。壓縮儲存:行優先一行一行掃 有效資料存
資料結構-稀疏矩陣(壓縮儲存,轉置,加法,乘法)類庫
上完資料結構課,練練手~ 個人能力問題,可能會有少許bug,畢竟本人debug這個程式碼用了2天的空閒時間... 目前本人測試沒有問題...記錄一下,方便以後整理,更新程式碼, debug。 ----------------- 程式碼用了兩個class分別封裝Matr
對稱矩陣壓縮儲存
下三角儲存i>=j,SymmetricMatrix[i][j] == Array[i*(i+1)/2+j]//壓縮儲存矩陣 template<class T> class Square { public:Square(T *arr,size_t N):_row(N), _col(N){siz
(重新放入原始碼)稀疏矩陣壓縮儲存及轉置,加法運算(採用三元表)
一、 實驗環境VC6.0, 二、 實驗目的 輸入任意兩個稀疏矩陣進入三元表,求出其加法運算後的矩陣,轉置矩陣,輸出矩陣。 三、 實驗內容1用C語言實現稀疏矩陣的三元組儲存結構 ;2實現稀疏矩陣的矩陣輸入、矩陣輸出等演算法;3.利用三元組儲存結構解決稀疏矩陣的運算問題(
資料結構:稀疏矩陣的壓縮儲存
問題提出:矩陣儲存壓縮 分析:儘可能地壓縮資料量;壓縮後仍然可以比較容易地進行各項基本操作. 兩類矩陣的壓縮儲存:特殊矩陣;稀疏矩陣. 稀疏矩陣的壓縮儲存思想: -儲存非零元:值;位置(行列號) -儲存適當的輔助資訊:行數;列數;非零元的個數 三元組<i,
特殊矩陣的壓縮儲存及轉置
一、對稱矩陣及其壓縮儲存 1、對稱矩陣 在矩陣中最特殊的一類應該屬於對稱矩陣,對稱矩陣的行和列是對應相等的。對稱矩陣就是關於主對角線對稱,兩邊的元素的值對應相等,在數學中我們把用主對角線隔開,一方全是0,一方是非零值的元素,分為上三角和下三角. 2、對稱矩陣的壓縮儲存 首先
棧:矩陣的壓縮儲存
概念: 科學與工程計算有一個特殊的數學物件,那就是矩陣。如何將矩陣中的各個元素儲存在計算機中,陣列就是一個很好的選擇。我們通常會遇到三種類型的矩陣: 普通矩陣 特殊矩陣:對稱矩陣、上三角矩陣、下三角矩陣、對角矩陣等 稀疏矩陣 特殊 特殊矩陣和稀疏
CF#462 div1 D:A Creative Cutout
無聊 一個 ive times play 得到 組合 命名 解釋 CF#462 div1 D:A Creative Cutout 題目大意: 原網址戳我! 題目大意: 在網格上任選一個點作為圓中心,然後以其為圓心畫\(m\)個圓。 其中第\(k\)個圓的半徑為\(\sqrt
資料結構例程——對稱矩陣的壓縮儲存及基本運算
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
對稱矩陣與壓縮儲存演算法(java實現)
一、問題描述 實現一個對稱矩陣的壓縮儲存 二、演算法分析 對稱矩陣的特點:a[i][j] = a[j][i].即所有元素關於對角線對稱 所以可以將對稱矩陣的下三角儲存在一個數組物件SA中,儲存方式是, SA[0] = a[0][0] SA[1] = a[1][0]