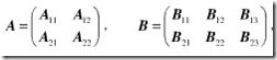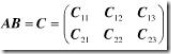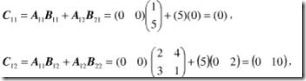1 Agent and Repository

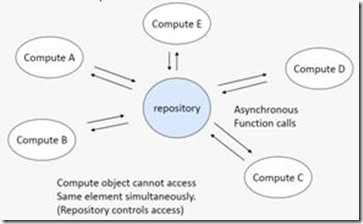
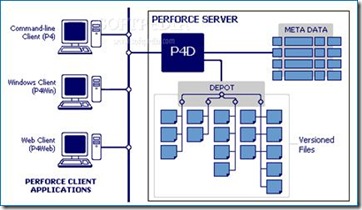
這是一個“架構模式”，它針對這樣一類問題：我們有一組資料，它們會隨機的被一些不同的物件進行修改。解決這一類問題的方案是，建立一個集中管理的資料倉庫（data repository），然後定義一組自治的agent來操作這些資料，可能還有一個manager來對agent的操作進行協調，並保證資料倉庫中資料的一致性。我們常見的原始碼版本控制軟體例如Perforce就是實現這種架構的典型代表：原始碼都存放在一個統一的伺服器中（或是一組伺服器中，但對client而言是透明的），不同的程式設計師們使用各自的客戶端對原始碼檔案進行讀，寫，加，刪的操作。由Perforce負責保證原始碼資料的一致性。

2 Map Reduce

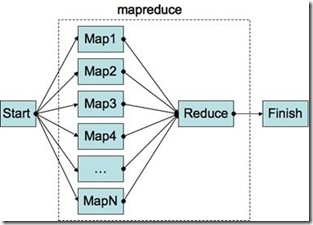
Map Reduce這個名詞原來是函數語言程式設計裡面的一個概念，但是自從Google於2004年推出同名的平行計算程式庫後，提到這個名詞大家大多想到的是Google的這個Framework。在這裡，Map Reduce是一個“架構模式”的名稱。當然，我們這裡的Map Reduce指的就是類似Google Map Reduce工作原理的一類模式。

那麼什麼是Map Reduce的模式呢？用較為簡單的語言描述，它指的是這樣一類問題的解決方案：我們可以分兩步來解決這類問題。第一步，使用一個序列的Mapper函式分別處理一組不同的資料，生成一箇中間結果。第二步，將第一步的處理結果用一個Reducer函式進行處理（例如，歸併操作），生成最後的結果。從使用Google的Map Reduce程式庫的角度而言，作為應用程式設計師，我們只需提供一組輸入資料，和兩個普通的序列函式（Mapper和Reducer），Google的Map Reduce框架就會接管一切，保證輸入資料有效的在一個分散式的計算機叢集裡面分配，然後Mapper和Reducer函式在其上有效的執行、處理，並最後彙總生成我們想要的處理結果。所有一切的細節，例如並行化、資料的分配、不同機器之間的計算誤差，通通被隱藏在程式庫內。

那麼Map Reduce到底是什麼樣的一個過程呢？

我們講過，使用Map Reduce，程式設計師必須提供一組輸入資料，以及一個Mapper和一個Reducer函式。在這裡，輸入資料必須是一個按(input_key,input_value)方式組織的列表。

mapper函式的任務是處理輸入列表中的某一個單元資料：mapper(input_key,input_value)，併產生如下輸出結果：

接下來，把對所有單元資料的處理結果按照intermediate_key歸類：同樣的intermediate_key放在一起，它們的intermediate_value簡單的串接起來，得到：

Reducer函式的任務是對上述的中間結果進行處理：reducer(intermediate_key, intermediate_value_list)，併產生如下最終輸出結果：

我們會舉兩個例子說明這一過程。第一個例子是一個簡單的統計單詞出現次數的小程式。第二個例子是Google曾經怎樣使用Map Reduce FrameWork來計算Page Rank。

第一個例子，假設我們要寫一個小程式，來統計在幾篇不同文章裡所有出現過的單詞各自總共出現的次數。我們應該怎麼做呢？下面描述的利用Map Reduce的方法肯定不是大多數程式設計師第一感會想到的方法。但這種方法非常好的揭示了Map Reduce的基本思想。並且，這種方法很容易被擴充套件到處理上千萬甚至是上億的檔案資料，並且能夠在一個分佈的計算機叢集裡面執行。這可不是傳統的方法能夠輕易做到的。

具體而言，假設我們有如下三個文字檔案，a.txt, b.txt和c.txt：

對於輸入資料而言，input_key就是檔名，input_value就是一個大的string，包含的是檔案內容。所以我們的輸入資料看上去會是這樣的：

我們會寫一個簡單的序列的mapper(fileName, fileContent)函式。這個函式做的事情很簡單，讀入一個文字檔案，把每一個遇到的單詞當作一個新的intermediate_key，並賦其intermediate_value為1。將mapper函式處理檔案a，我們會得到如下結果：

將所有三個檔案的處理結果放在一起，我們得到：

然後將中間結果按intermediate_key歸類：

最後，由reducer(intermediate_key, intermediate_value_list)對中間結果進行處理。它做的事也很簡單，僅僅是把某intermediate_key對應的所有intermediate_value相加。我們於是得到最終結果:

第二個例子，怎樣使用Map Reduce計算PageRank。什麼是PageRank？可能大家都有所瞭解，這是Google用來量度一個網頁的重要性的值。簡單而言，有越多的其它網頁連結到這個網頁，這個網頁的PageRank越高。連結到這個網頁的網頁PageRank越高，這個網頁的PageRank也越高。假設我們一共有n個網頁0, 1, …, n-1。對第j個網頁我們給它賦一個PageRank值q_j。所有的q_j組合起來成為一個向量q = (q₀,q₁, …q_n-1)。這個向量滿足概率分佈。即q_j的值都在0和1之間，並且所有的q_j加起來等於1。q_j越大，網頁的重要性越高。那麼q是怎麼計算出來的呢？答案是使用迭代的方法： 

我們從一個初始的PageRank向量分佈P開始，乘以一個n*n的矩陣M，得到一個新的PageRank向量。把新的PageRank向量繼續乘以M得到下一步的PageRank… … 如此迭代有限步後，PageRank向量的值會趨於收斂，於是我們得到最終的PageRank。

這裡需要回答兩個問題：1. 如何確定初始的PageRank，即迭代的起點？答案是任意選擇一個概率分佈就可以，無論你選擇什麼初始值，都不影響其收斂到最終的結果。我們通常使用均勻概率分佈，即。2. 如何定義M？這個問題稍顯複雜，有興趣的讀者可以參見Michael Nielsen 的博文Using MapReduce to compute PageRank瞭解更詳細的內容。在這裡，我們將其簡化的定義為一個描述網頁間互相連結結構的超大矩陣。假設網路裡有n個網頁，那麼我們這個矩陣就是一個n*n的方陣。矩陣的每一列代表一個網頁對外的超連結情況。例如，我們定義#(j)為第j個網頁對外的所有超連結的數量。那麼對於矩陣M的第j列而言，如果網頁j對網頁k沒有超連結，那麼第k行元素M_kj=0，否則M_kj=1/#(j)。這裡隱含的意思是當一個讀者在瀏覽網頁j時，有1/#(j)的可能性跳轉到網頁k。

那麼如何使用Map Reduce來計算PageRank呢？雖然整個迭代的過程必須是序列的，迭代的每一步我們還是可以用Map Reduce來並行的計算的。這裡也必須並行的計算因為這個矩陣和向量的規模是超大的（想象一下整個網際網路的網頁數量）。使用Map Reduce來計算迭代的一步實際上是用Map Reduce來計算矩陣和向量的乘法。假設我們要計算如下一個方陣和向量的乘法。其實質是將第i個向量元素的值p_i乘以矩陣第i列的每一元素，然後放在矩陣元素原來的位置。最後，把矩陣第i行的所有元素相加，得到結果向量的第i個元素的值。

類似的，我們可以得到用MapReduce計算PageRank的方法：

第一步，輸入的(input_key, input_value)。input_key是某個網頁的編號，如j。input_value是一個列表，元素值是M矩陣的第j列元素，最後再加上一個p_j，就是當前網頁j的PageRank值。

第二步，Map。Mapper(input_key, input_value)所做的事情很簡單，就是把p_j乘以列表元素的每一個值，然後輸出一組(intermediate_key, intermediate_value)。intermediate_key就是矩陣的行號，k。intermediate_value就是p_j列表元素的值，即p_j乘以矩陣第k行第j列的元素的值。

第三步，彙總。把所有intermediate_key相同的中間結果放到一起。即是把第k行所有的intermediate_value放在一個列表intermediate_value_list內。

第四步，Reduce。Reducer(intermediate_key, intermediate_value_list)做的事也很簡單，就是把intermediate_value_list內所有的值相加。最後形成的(output_key, output_value)就是結果向量第k行的元素值。

以上就是利用Map Reduce計算PageRank的簡略過程。這個過程相當粗略和不精確，只是為了揭示Map Reduce的工作過程和Google曾經用來計算PageRank的大致方法。認真的讀者應該查閱其它更嚴謹的著作。

最後，和上述計算矩陣和向量乘法的例子相似，Map Reduce也可以用來計算兩個向量的點乘。具體怎麼做留給讀者自己去思考，一個提示是我們所有的intermediate_key都是相同的，可以取同一個值例如1。

3 Data Parallelism

這是一個“演算法模式”。事實上，把Data Parallelism和下節將要提到的Task Parallelism都稱之為一種“演算法模式”我覺得有過於籠統之嫌。到最後，哪一種並行演算法不是被分解為並行執行的task呢（task parallelism）？ 而並行執行的task不都是處理著各自的那份資料嗎（data parallelism）？所以如果硬要把Data Parallelism和Task Parallelism稱為兩種演算法模式，我只能說它們的地位要高於其它的演算法模式。它們是其它演算法模式的基礎。只不過對於有些問題而言，比較明顯的我們可以把它看成是Data Parallelism的或是Task Parallelism的。也許Data Parallelism模式和Task Parallelism模式特指的就是這類比較明顯的問題。

那麼什麼是Data Parallelism? 顧名思義，就是這類問題可以表達為同樣的一組操作被施加在不同的相互獨立的資料上。

一個比較典型的例子就是計算機圖形學裡面的Ray tracing演算法。Ray tracing演算法可以大致描述為從一個虛擬相機的光心射出一條射線，透過螢幕的某個畫素點，投射在要渲染的幾何模型上。找到射線和物體的交點後，再根據該點的材料屬性、光照條件等，算出該畫素點的顏色值，賦給螢幕上的畫素點。由於物體的幾何模型很多個小的三角面片表示，演算法的第一步就是要求出射線與哪個三角面片有交點。射線與各個單獨的三角面片求交顯然是相互獨立的，所以這可以看做是Data Parallelism的例子。

4 Task Parallelism

Task Parallelism的演算法模式可以表述為，一組互相獨立的Task各自處理自己的資料。和Data Parallelism不同，這裡關注的重點不是資料的劃分，而是Task的劃分。

如前所述，Task Parallelism和Data Parallelism是密不可分的。互相獨立的Task肯定也是執行在互相獨立的資料上。這主要是看我們以什麼樣的視角去看問題。例如，上一節RayTracing的例子中，我們也可以把射線和一個獨立的三角面片求交看作是一個獨立的Task。這樣就也可以當它做是Task Parallelism的例子。然而，咬文嚼字的去區分到底是Task Parallelism還是Data Parallelism不是我們的目的，我們關注的應該是問題本身。對於某一個具體問題，從Data Parallelism出發考慮方便還是從Task Parallelism出發考慮方便，完全取決於問題本身的應用場景以及設計人員自身的經驗、背景。事實上，很多時候，不管你是從Task Parallelism出發還是從Data Parallelism出發，經過不斷的優化，最終的解決方案可能是趨同的。

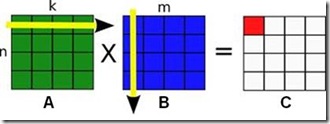
下面一個矩陣乘法的例子很好的說明了這個問題。我們都知道矩陣乘法的定義：假如有n行k列的矩陣A乘以k行m列的矩陣B，那麼我們可以得到一個n行m列的的矩陣C。矩陣C的第n行第m列的元素的值等於矩陣A的第n行和矩陣B的第m列的點乘。

從Task Parallelism的角度出發，我們可能把計算C的每一個元素當做一個獨立的Task。接下來，為了提高CPU的快取利用率，我們可能把鄰近幾個單元格的計算合併成一個大一點的Task。從Data Parallelism的角度出發，我們可能一開始把C按行分成不同的塊。為了探索到底怎樣的劃分更加有效率，我們可能調整劃分的方式和大小，最後，可能發現，最有效率的做法是把A，B，C都分成幾個不同的小塊，進行分塊矩陣的乘法。可以看到，這個結果實際上和從Task Parallelism出發考慮的方案是殊途同歸的。

5 Recursive Splitting

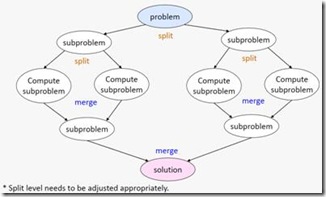
Recursive Splitting指的是這樣一種演算法模式：為了解決一個大問題，把它分解為可以獨立求解的小問題。分解出來的小問題，可能又可以進一步分解為更小的問題。把問題分解到足夠小的規模後，就可以直接求解了。最後，把各個小問題的解合併為原始的大問題的解。這實際上是我們傳統的序列演算法領域裡面也有的“divide and conquer”的思想。

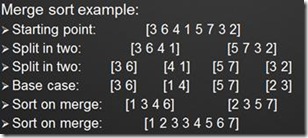
舉兩個例子。第一個是傳統的歸併排序。例如，要排序下面的8個元素的陣列，我們不管三七二十一先把它一分為二。排序4個元素的陣列還是顯得太複雜了，於是又一分為二。現在，排序2個元素的陣列很簡單，按照大小交換順序就行。最後，把排好序的陣列按序依次組合起來，就得到我們最終的輸出結果。

第二個例子稍微有趣一點，是一個如何用程式解“數獨”遊戲的例子。“數獨”就是在一個9*9的大九宮格內有9個3*3的小九宮格。裡面有些格子已經填入了數字，玩家必須在剩下的空格里也填入1到9的數字，使每個數字在每行、每列以及每個小九宮格內只出現一次。

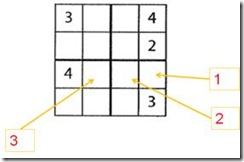
這裡作為舉例說明，我們考慮一個簡單一點的情況：在一個4*4的格子裡填入1~4的數字，使其在每行、每列以及每個2*2的格子裡只出現一次。

解“數獨”遊戲的演算法可以有很多種。如果是人來解，大概會按照上圖的次序依次填入1,2,3到相應的格子當中。每填入一個新數字，都會重新按規則評估周圍的空格，看能否按現有情況再填入一些數字。這個方法當然沒錯，不過看上去不太容易並行化。下面介紹一個按照“recursive splitting”的方法可以很容易做到並行化的解法。

1） 首先，將二維的數獨格子展開成一個一維的陣列。已經有數字的地方是原來的數字，空格子的地方填上“0”。 

2） 接下來，從前到後對陣列進行掃描。第一格是“3”，已經有數字了，跳過。移動搜尋指標到下一格。

3） 第二格是“0”，意味著我們需要填入一個新的數字。這個新的數字有4種可能性：1， 2， 3， 4。所以建立4個新的搜尋分支：

4） 接下來根據現有的數字資訊檢查各個搜尋分支。明顯，第三和第四個搜尋分支是非法的。因為我們在同一行中已經有了數字“3”和“4”。所以忽略這兩個分支。第一和第二條分支用現有的數字檢查不出衝突，所以繼續從這兩個分支各派生出4條新的分支進行搜尋… …

這個思路像極了我們之前的歸併排序的例子，都是在演算法執行的過程中不斷產生出新的任務。所以實際上這也是一個“Task Parallelism”的例子。

6 Pipeline

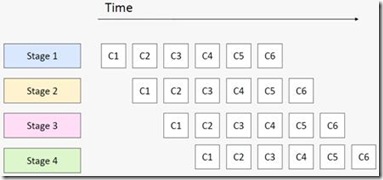
“Pipeline”也是一種比較常見的演算法模式。通常，我們都會用汽車裝配中的流水線、CPU中指令執行的流水線來類比的說明這一模式。它說的是我們會對一批資料進行有序、分階段的處理，前一階段處理的輸出作為下一階段處理的輸入。每一個階段永遠只重複自己這一階段的任務，不停的接受新的資料進行處理。用一個軟體上的例子打比方，我們要開啟一批文字檔案，將裡面每一個單詞的字母全部改成大寫，然後寫到一批新的檔案裡面去，就可以建立一條有3個stage的流水線：讀檔案，改大寫，寫檔案。

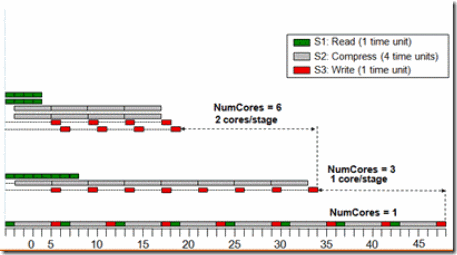
“Pipeline”模式的概念看上去很容易理解，可是也不是每一個人都能一下子理解的那麼透徹的。例如有這樣一個問題：我們有一個for迴圈，迴圈體是一條有3個stage的pipeline，每個stage的執行時間分別是10， 40， 和10個CPU的時鐘間隔。請問這個for迴圈執行N次大概需要多長時間（N是一個很大的數）？

A. 60*N

B. 10*N

C. 60

D. 40*N

請仔細思考並選擇一個答案。:-)

答案是40*N。流水線總的執行時間是由它最慢的一個stage決定的。原因請見下圖。

7 Geometric decomposition

接下來這兩個演算法模式看上去都顯得比較特殊化，只針對某些特定的應用型別。“Geometric decomposition”說的是對於一些線性的資料結構（例如陣列），我們可以把資料切分成幾個連續的子集。因為這種切分模式看上去和把一塊幾何區域切分成連續的幾塊很類似，我們就把它叫做”Geometric decomposition”。

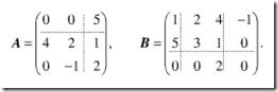
最常用的例子是分塊矩陣的乘法。例如，為了計算兩個矩陣A，B的乘法。我們可以把他們切分成各自可以相乘的小塊。

結果矩陣當然也是分塊的：

結果矩陣每一分塊的計算按照如下公式進行：

例如：

最終的結果就是：

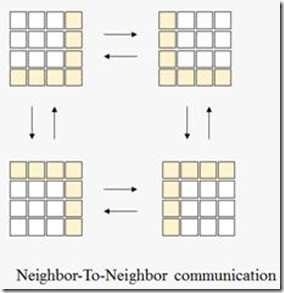
下面這幅圖顯示了兩個4*4的分塊矩陣A，B進行乘法時，計算結果矩陣C的某一分塊時，需要依次訪問的A，B矩陣的分塊。黑色矩陣分塊代表要計算的C的分塊，行方向上的灰色矩陣代表要訪問的矩陣A的分塊，列方向上的灰色分塊代表要訪問的矩陣B的分塊。

8 Non-work-efficient Parallelism

這個模式的名字取得很怪異，也有其他人把它叫做“Recursive Data”。不過相比而言，還是這個名字更為貼切。它指的是這一類模式：有些問題的處理使用傳統的方法，必須依賴於對資料進行有序的訪問，例如深度優先搜尋，這樣就很難並行化。但是假如我們願意花費一些額外的計算量，我們就能夠採用並行的方法來解決這個問題。

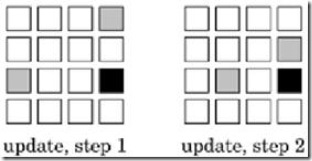
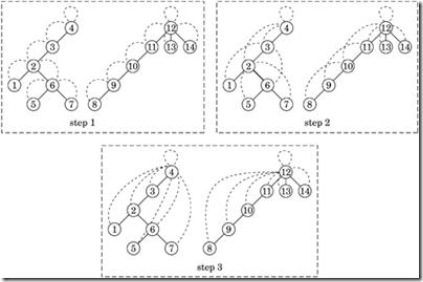
常用的一個例子是如下的“尋找根節點”的問題。假設我們有一個森林，裡面每一個節點都只記錄了自己的前向節點，根節點的前向節點就是它自己。我們要給每一個節點找到它的根節點。用傳統的方法，我們只能從當前節點出發，依次查詢它的前向節點，直到前向節點是它自身。這種演算法對每一個節點的時間複雜度是O(N)。總的時間複雜度是N*O(N)。

如果我們能換一種思路來解這個問題就可以將其並行化了。我們可以給每一個節點定義一個successor（後繼結點），successor的初始值都是其前向節點。然後我們可以同步的更新每一個節點的successor，令其等於“successor的successor”，直到successor的值不再變化為止。這樣對於上圖的例子，最快兩次更新，我們就可以找到每個節點的根節點了。這種方法能同時找到所有節點的根節點，總的時間複雜度是N*log (N)。

原帖：

http://www.cnblogs.com/kaige/archive/2012/04/10/2439823.html