在機器學習中，經常需要對模型進行正則化，以降低模型對資料的過擬合程度，那麼究竟如何理解正則化的影響？本文嘗試從視覺化的角度來解釋其影響。

首先，正則化通常分為三種,都是在loss函式的基礎上外加一項：

L0：  ，即不等於0的元素個數

L1：  ，即所有元素的絕對值之和

L2：  ，即所有元素的絕對值平方和

訓練模型的時候，模型將在保證loss主體損失下降的情況下，儘量保證權重往這些方向走，從L1,L2的函式中就可以看出，在做梯度下降的時候，這些函式都將把權重趕向接近0的地方，讓權重變得更加稀疏，大部分資料都在0附近。

從最小化結構風險的角度來看（這個和奧卡姆剃刀律有異曲同工之妙），在多個模型中，我們選擇最簡單的那個模型作為最好的模型，而不是最複雜的，權重分佈最離散的那個。

從人類的角度來看，神經元（千億量級）的連線是極為稀疏的，平均每個神經元不超過十萬，這與總的神經元個數之間有極大的差距（至少六個數量級的差距），因此從先驗的角度來看，我們最好訓練一個連線極少（權重0極多）的模型才接近人類大腦。

可惜，L0正則化是一個NP難問題，我們很難保證準確率的前提下，挑選哪些元素是0，哪些不是，因此，一般我們用L1替代L0（具體為什麼我也不清楚.....但是效果是挺好）

為了更好地理解將權重趕向0的過程，我在mnist上訓練一個經典的CNN分類器，提取出所有的權重，求出其分佈來看看。（所有權重初始化為均值0，方差0.5的正態分佈）

下面是圖片（正則化強度均為1e-4）：

無正則化

L1正則化

L2正則化

從中我們能得到什麼資訊呢？

1. L1L2正則化如實地將權重往0的方向趕，但是L1趕得快，L2比較慢一些，在30epoch以上L2才有類似於L1的一枝獨秀的分佈。

2. 在測試集上，沒有正則化，L1,L2正則化的準確率基本都一樣（有正則化的略高），這樣一來，在保證準確率的前提下，L1L2正則化能夠省下更多的元素，這就意味著模型能夠大大地減少其儲存空間（將矩陣變成稀疏矩陣的形式儲存）

為了解釋這個問題，我們可以回到L1,L2的函式影象來看。元素絕對值在[0,1]之間的時候，L1對於元素的懲罰更大，L2的懲罰小，相對的容忍度更大。元素絕對值在[1，∞]之間的時候，L1對於元素的懲罰更小，L2的懲罰大，相對的容忍度更小。

從斜率角度來看，L2正則化的斜率大要在[1，∞]才能發揮其功力，在[0,1]之間，往0趕的能力不是很強。然而L1在所有地方斜率都一樣，相對而言，在[0,1]之間，其往0趕的能力強。

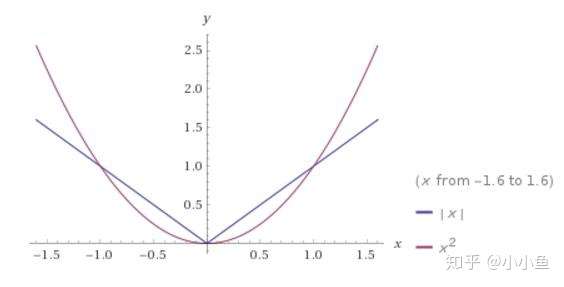
L1與L2正則化

彩蛋：

事實上Keras允許自定義正則化函式，我們也可以多定義幾種正則化方式玩玩：

詭異的L3正則化，可能是三次方往0趕的能力實在太差，多數元素都在0附近徘徊所致

L3正則化，函式y=|x|^3

有死區的L1，在-a到a之間沒有懲罰，效果類似於L1，也能讓0更多（還有為啥loss小於0了.......）

有死區的L1，函式y=max(0,|x|-a)，其中a=0.25

程式碼：

from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential,Model
from keras.layers import Dense, Dropout, Flatten,Input
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
from keras import initializers
import numpy as np
import matplotlib.pyplot as plt
from keras import regularizers
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], 28, 28,1)
x_test = x_test.reshape(x_test.shape[0], 28, 28,1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255.0
x_test /= 255.0
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)
def my_reg(weight_matrix):
    return 1e-4 * K.sum(K.max(K.abs(weight_matrix) - 0.25,0))
    #return 1e-4 * K.sum(K.pow(K.abs(weight_matrix),2))

init = initializers.random_normal(mean=0,stddev=0.25,seed=42)
input = Input(shape=(28,28,1))
conv1 = Conv2D(32, kernel_size=(3, 3),activation='relu',kernel_initializer=init,kernel_regularizer=my_reg)(input)
conv2 = Conv2D(64, (3, 3), activation='relu',kernel_initializer=init,kernel_regularizer=my_reg)(conv1)
pool1 = MaxPooling2D(pool_size=(2, 2))(conv2)
conv3 = Conv2D(128, (3, 3), activation='relu',kernel_initializer=init,kernel_regularizer=my_reg)(pool1)
pool2 = MaxPooling2D(pool_size=(2, 2))(conv3)
flat = Flatten()(pool2)
dense1 = Dense(128, activation='relu',kernel_initializer=init,kernel_regularizer=my_reg)(flat)
output = Dense(10, activation='softmax',kernel_initializer=init,kernel_regularizer=my_reg)(dense1)
model = Model(inputs=input,outputs=output)
model.compile(loss=keras.losses.categorical_crossentropy,optimizer=keras.optimizers.Adadelta(),metrics=['accuracy'])
model.summary()

for i in range(40):
    model.fit(x_train, y_train, batch_size=128, epochs=1, verbose=0, validation_data=(x_test, y_test))
    score = model.evaluate(x_test, y_test, verbose=0)
    weights = model.get_weights()
    all_weights = np.zeros([0, ])
    for w in weights:
        w_flatten = np.reshape(w, [-1])
        all_weights = np.concatenate([all_weights, w_flatten], axis=0)
    plt.hist(all_weights, bins=100,color="b",normed=True,range=[-1,1])
    plt.title("epoch="+str(i)+" loss=%.2f ,acc=%.3f"%(score[0],score[1]))
    plt.savefig("mnist_model_weights_hist_%d.png"%(i))
    plt.clf()

參考文獻：

[1]Stephen Boyd，凸優化Convex Optimization,清華大學出版社，286-290

[2]Ian Goodfellow，深度學習Deep Learning，人民郵電出版社,141-145