2. 程式人生 > >leetcode--二叉樹和圖

leetcode--二叉樹和圖

阿新 • • 發佈：2019-02-04

基礎知識

二叉樹的資料結構

struct TreeNode{
    int val;   //資料域
    TreeNode *left //左右指標
    TreeNode *right
    TreeNode(int x):val(x),left(NULL),right(NULL){}
    //建構函式
}

構造二叉樹

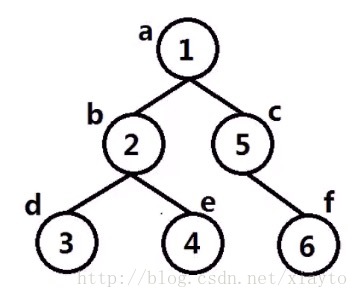
構造如下的一棵二叉樹：
二叉樹

int main(){
    TreeNode a(1);
    TreeNode b(2);
    TreeNode c(3);
    TreeNode d(4);
    TreeNode e(5);
    TreeNode f(6
 
);
    a.left=&b;
    a.right=&c;
    b.left=&d;
    b.right=&e;
    c.right=&f;
}

二叉樹的深度遍歷

前序遍歷訪問
traversal(node->left)
中序遍歷訪問
traversal(node->right)
後序遍歷訪問

前中後指的是訪問根節點的順序，前序：先根再左再右

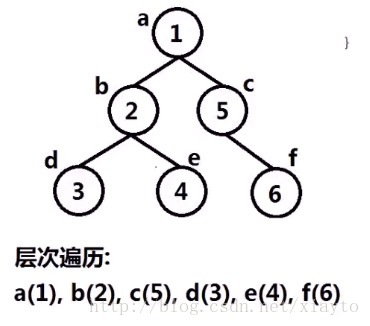
二叉樹的層次遍歷

也就是廣度優先搜尋，用佇列一層一層的訪問節點，訪問一個節點壓入該節點的孩子節點，佇列不空，持續該過程。
這裡寫圖片描述

void BFS_print(TreeNode* root){
    queue
 
<TreeNode*> Q;
    Q.push(root);
    while(!Q.empty()){
        TreeNode* node=Q.front();
        Q.pop();
        printf("(%d)\n",node->val);
        if(node->left){
            Q.push(node->left;
        }
        if(node->right){
            Q.push(node->right;
        }
    }
}

leetcode題目

113 Path Sum

題意：

給定一個二叉樹與整數sum，找出所有從根節點到葉節點的路徑，要求這些路徑上節點值的和等於sum。

解題思路：

用深度優先搜尋路徑。
1 先序遍歷時將節點值儲存到path棧中，path_value累加節點值
2 當遍歷到葉節點時判斷path_value是不是等於sum，if等於push進result中。
3 在後序遍歷時，將節點從path棧中彈出，path_value減去節點值

程式碼：

class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<vector<int>> result;
        vector<int> path;
        int path_value=0;
        preorder(root,path_value,sum,path,result);
        return result;
    }
private:
    void preorder(TreeNode *node,int &path_value,int sum,vector<int> &path,vector<vector<int>> &result){
        //先序遍歷內容：
        if(!node){
            return;
        }
        path_value=path_value+node->val;
        path.push_back(node->val);
        if(!node->left&&!node->right&&path_value==sum){
            result.push_back(path);
        }
        preorder(node->left,path_value,sum,path,result);
        preorder(node->right,path_value,sum,path,result);
        //後序遍歷內容:
        path.pop_back();
        path_value=path_value-node->val;
    }
};

236 Lowest Common Ancestor of a Binary Tree

題意：

給出兩個節點，求出他們最近的公共祖先。

解題思路：

1 用深度優先搜尋找點，找到點後儲存路徑。
2 同時遍歷兩個路徑，找最後一個相同點。

程式碼：

void preorder(TreeNode* node,
              TreeNode *search,
              std::vector<TreeNode*> &path,
              std::vector<TreeNode*> &result,
              int &finish){
    if (!node || finish){
        return;      //結束技巧，finish用於標記已找到節點
    }
    path.push_back(node);
    if (node == search){
        finish = 1;
        result = path;
    }
    preorder(node->left, search, path, result, finish);
    preorder(node->right, search, path, result, finish);
    path.pop_back();//後序遍歷時根節點要做退出操作，就是左右節點都不是要找的點，根節點彈出
}

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        std::vector<TreeNode*> path;
        std::vector<TreeNode*> node_p_path;
        std::vector<TreeNode*> node_q_path;
        int finish = 0;
        preorder(root, p, path, node_p_path, finish);//找p點的路徑並保存於node_p_path
        path.clear();
        finish = 0;
        preorder(root, q, path, node_q_path, finish);//找q點的路徑並保存於node_q_path
        int path_len = 0;
        if (node_p_path.size() < node_q_path.size()){
            path_len = node_p_path.size();
        }
        else{
            path_len = node_q_path.size();
        }
        TreeNode *result = 0;
        //找兩個路徑中最後一個相同點
        for (int i = 0; i < path_len; i++){
            if (node_p_path[i] == node_q_path[i]){
                result = node_p_path[i];//少寫一點程式碼
            }
        }
        return result;
    }
};

114. Flatten Binary Tree to Linked List

題意：

不用大的額外空間，將二叉樹轉換為連結串列，left為null，right為連結串列的next指標。連結串列的順序是樹的先序遍歷。

解題思路：

如果不考慮大的額外空間，最簡單的做法是用一個vector存先序遍歷的結果，然後遍歷這個vector。

程式碼：

class Solution {
public:
    void flatten(TreeNode *root) {
        std::vector<TreeNode *> node_vec;
        preorder(root, node_vec);
        for (int i = 1; i < node_vec.size(); i++){
            node_vec[i-1]->left = NULL;
            node_vec[i-1]->right = node_vec[i];
        }
    }
private:
    void preorder(TreeNode *node,vector<TreeNode *> &node_vec){
        if (!node){
            return;
        }
        node_vec.push_back(node);
        preorder(node->left, node_vec);
        preorder(node->right, node_vec);
    }
};

解題思路2：

思考過程是：獨立開樹的一部分，思考前中後遍歷時候應該做什麼。考慮輸入和輸出:
* 先序遍歷：第一次訪問根節點時，我們要保留左右節點，讓right指標指向左節點。右指標指向NULL。
* 中序遍歷：第二次訪問根節點，這時左子樹完成了連結串列變形，要將左子樹的最後節點指向，右子樹的開始節點。所以要輸出一個末尾節點，可以用&引用去維護。
* 後續遍歷：維護最末的節點。

程式碼：

class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode *last=NULL;
        preorder(root,last);
    }
private:
    void preorder(TreeNode* node,TreeNode* &last){
        //*& TreeNode*的意思是傳入TreeNode的指標變數，&是可以在函式中改變這個變數
        if(!node){
            return;
        }
        if(!node->left&&!node->right){
            last=node;
            return;
        }
        TreeNode* left=node->left; //保留左右節點
        TreeNode* right=node->right;
        TreeNode* left_last=NULL;//初始化要維護的末尾節點。
        TreeNode* right_last=NULL;
        if(left){
            preorder(left,left_last);//遞迴，維護左子樹的末尾節點
            node->left=NULL; //放在中序遍歷執行時因為可以省去判斷是否有左子樹的語句。
            node->right=left;
            last=left_last;
        }
        if(right){
            preorder(right,right_last);
            if(left_last){
                left_last->right=right;//讓左子樹的末尾節點指向右子樹的開始節點。放在後序遍歷執行可以省去判斷是否有右子樹的語句。
            }
            last=right_last;//維護右子樹的末尾節點
        }
    }
};

199.Binary Tree Right Side View

題意：

從右邊觀察二叉樹，輸出每一層最右邊的節點。

解題思路：

層次遍歷二叉樹，將節點和層數繫結微pair，壓入佇列時，將節點和層數同時壓入，記錄每一層的最後一個節點。

程式碼：

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> view; //儲存每層最後的節點。
        queue<pair<TreeNode*,int>> Q;
        //廣度優先搜尋，用一個pair儲存節點和它對應的層數。
        if(root){
            Q.push(make_pair(root,0));
        }
        while(!Q.empty()){
            TreeNode* node=Q.front().first;  
            int depth=Q.front().second;
            Q.pop();
            if(view.size()==depth){
                view.push_back(node->val); //當出現新的層時壓入一個節點。
            }
            else{
                view[depth]=node->val;
            }
            if(node->left){
                Q.push(make_pair(node->left,depth+1));  //壓入左節點，標記為下一層
            }
            if(node->right){
                Q.push(make_pair(node->right,depth+1)); //壓入右節點，標記為下一層
            }
        }
        return view;
    }
};

圖

圖

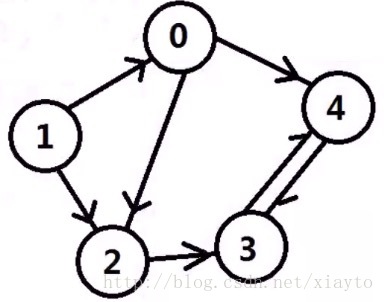
圖的表示（鄰接矩陣）：

這裡寫圖片描述

程式碼：

int main(){
    const int MAX_N = 5;
    int Graph[MAX_N][MAX_N] = {0};
    Graph[0][2] = 1;
    Graph[0][4] = 1;
    Graph[1][0] = 1;
    Graph[1][2] = 1;
    Graph[2][3] = 1;
    Graph[3][4] = 1;
    Graph[4][3] = 1;
    printf("Graph:\n");
    for (int i = 0; i < MAX_N; i++){
        for (int j = 0; j < MAX_N; j++){
            printf("%d ", Graph[i][j]);
        }
        printf("\n");
    }
    return 0;
}

表示稠密圖作用比較大，但是表示稀疏圖一般用鄰接表。

圖的表示（鄰接表）：

這裡寫圖片描述

程式碼：

#include <stdio.h>
#include <vector>

struct GraphNode{
    int label;
    std::vector<GraphNode *> neighbors;
    GraphNode(int x) : label(x) {};
};

int main(){ 
    const int MAX_N = 5;
    GraphNode *Graph[MAX_N];

    for (int i = 0; i < MAX_N; i++){
        Graph[i] = new GraphNode(i);
    }

    Graph[0]->neighbors.push_back(Graph[2]);
    Graph[0]->neighbors.push_back(Graph[4]);
    Graph[1]->neighbors.push_back(Graph[0]);
    Graph[1]->neighbors.push_back(Graph[2]);
    Graph[2]->neighbors.push_back(Graph[3]);
    Graph[3]->neighbors.push_back(Graph[4]);
    Graph[4]->neighbors.push_back(Graph[3]);

    printf("Graph:\n");
    for (int i = 0; i < MAX_N; i++){
        printf("Label(%d) : ", i);
        for (int j = 0; j < Graph[i]->neighbors.size(); j++){
            printf("%d ", Graph[i]->neighbors[j]->label);
        }
        printf("\n");
    }
    for (int i = 0; i < MAX_N; i++){
        delete Graph[i];
    }
    return 0;
}

深度優先搜尋

struct GraphNode{
    int label;
    std::vector<GraphNode *> neighbors;
    GraphNode(int x) : label(x) {};
};

void DFS_graph(GraphNode *node, int visit[]){
    visit[node->label] = 1;
    printf("%d ", node->label);
    for (int i = 0; i < node->neighbors.size(); i++){
        if (visit[node->neighbors[i]->label] == 0){
            DFS_graph(node->neighbors[i], visit);
        }
    }
}

廣度優先搜尋

struct GraphNode{
    int label;
    std::vector<GraphNode *> neighbors;
    GraphNode(int x) : label(x) {};
};

void BFS_graph(GraphNode *node, int visit[]){
    std::queue<GraphNode *> Q;
    Q.push(node);
    visit[node->label] = 1;
    while(!Q.empty()){
        GraphNode *node = Q.front();
        Q.pop();
        printf("%d ", node->label);
        for (int i = 0; i < node->neighbors.size(); i++){
            if (visit[node->neighbors[i]->label] == 0){
                Q.push(node->neighbors[i]);
                visit[node->neighbors[i]->label] = 1;
            }
        }
    }
}

leetcode題目

207. Course Schedule

題意：給出課程之間的依賴關係，求是否可以將所有的課程全部完成。其實就是求有向圖是否有環。

解題思路一：

  • 用深度優先搜尋，如果遞迴搜尋某一條路徑時發現路徑中有重複的節點，則有環，不能完成。
  • 這裡的visit的陣列要設計三種狀態：-1是未被搜尋，0是正在被搜尋的路徑上，1是已經完成搜尋的節點。
  • 像遞迴二叉樹思考方式一樣，思考先序中序後序遍歷要進行什麼操作：
    • 先序遍歷：將該節點標記狀態visit為0
    • 中序遍歷：如果訪問過程中出現訪問到visit為0的點則返回false
    • 後續遍歷：訪問完成將該節點標記狀態visit為-1

程式碼：

struct GraphNode{
    int label;
    std::vector<GraphNode *> neighbors;
    GraphNode(int x) : label(x) {};
};
bool DFS_graph(GraphNode *node, std::vector<int> &visit){
    visit[node->label] = 0;
    for (int i = 0; i < node->neighbors.size(); i++){
        if (visit[node->neighbors[i]->label] == -1){
            if (DFS_graph(node->neighbors[i], visit) == 0){
                return false;
            }
        }
        else if (visit[node->neighbors[i]->label] == 0){
            return false;
        }
    }
    visit[node->label] = 1;
    return true;
}

class Solution {
public:
    bool canFinish(int numCourses,
        std::vector<std::pair<int, int> >& prerequisites) {
        std::vector<GraphNode*> graph;
        std::vector<int> visit;
        for (int i = 0; i < numCourses; i++){
            graph.push_back(new GraphNode(i));
            visit.push_back(-1);
        }
        for (int i = 0; i < prerequisites.size(); i++){
            GraphNode *begin = graph[prerequisites[i].second];
            GraphNode *end = graph[prerequisites[i].first];
            begin->neighbors.push_back(end);
        }
        for (int i = 0; i < graph.size(); i++){
            if (visit[i] == -1 && !DFS_graph(graph[i], visit)){
                return false;
            }
        }
        for (int i = 0; i < numCourses; i++){
            delete graph[i];
        }
        return true;
    }
};

解題思路二：

用廣度優先搜尋，用入度的概念，每次只將入度為0的點壓入佇列，它指向的所有節點的入度都-1，-1後入度為0的點可以壓入佇列，如果能遍歷整個圖，則可以完成，不能遍歷則不能完成。

程式碼：

struct GraphNode{
    int label;
    std::vector<GraphNode *> neighbors;
    GraphNode(int x) : label(x) {};
};

class Solution {
public:
    bool canFinish(int numCourses,
        std::vector<std::pair<int, int> >& prerequisites) {
        std::vector<GraphNode*> graph;
        std::vector<int> degree;
        for (int i = 0; i < numCourses; i++){
            degree.push_back(0);
            graph.push_back(new GraphNode(i));
        }
        for (int i = 0; i < prerequisites.size(); i++){
            GraphNode *begin = graph[prerequisites[i].second];
            GraphNode *end = graph[prerequisites[i].first];
            begin->neighbors.push_back(end);
            degree[prerequisites[i].first]++;
        }       
        std::queue<GraphNode *> Q;
        for (int i = 0; i < numCourses; i++){
            if (degree[i] == 0){
                Q.push(graph[i]);
            }
        }
        while(!Q.empty()){
            GraphNode *node = Q.front();
            Q.pop();
            for (int i = 0; i < node->neighbors.size(); i++){
                degree[node->neighbors[i]->label]--;
                if (degree[node->neighbors[i]->label] == 0){
                    Q.push(node->neighbors[i]);
                }
            }
        }       
        for (int i = 0; i < graph.size(); i++){
            delete graph[i];
        }       
        for (int i = 0; i < degree.size(); i++){
            if (degree[i]){
                return false;
            }
        }
        return true;
    }
};

相關推薦

leetcode--二叉樹和圖

基礎知識 二叉樹的資料結構 struct TreeNode{ int val; //資料域 TreeNode *left //左右指標 TreeNode *right TreeNode(int x):val(x),

算法學習筆記（六） 二叉樹和圖遍歷—深搜 DFS 與廣搜 BFS

創建 mark preorder 第一個 高度 變量初始化 term link 文章 圖的深搜與廣搜 復習下二叉樹、圖的深搜與廣搜。從圖的遍歷說起。圖的遍歷方法有兩種：深度優先遍歷(Depth First Search),

LeetCode——中級演算法——樹和圖——二叉樹的鋸齒形層序遍歷（JavaScript）

給定一個二叉樹，返回其節點值的鋸齒形層次遍歷。（即先從左往右，再從右往左進行下一層遍歷，以此類推，層與層之間交替進行）。 例如： 給定二叉樹 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回鋸

[leetcode]二叉樹的最大深度和最小深度

一、二叉樹的最大深度 題目描述： Given a binary tree, find its maximum depth. The maximum depth is the number of nodes along the longest path from the root node d

二叉樹和廣義表的轉換

def har out char emp typedef con 逗號 字符串 1 //廣義表轉二叉樹： 2 設置一個標記變量k，初始值為-1； 3 設置一個標記結點p； 4 循環遍歷廣義表的字符串str； 5 如果str[i]是左括號：

(2)Java數據結構--二叉樹 -和排序算法實現

運行 至少 exceptio 子節點 註釋 heapsort borde 搜索樹 選擇排序 === 註釋：此人博客對很多個數據結構類都有講解-並加以實例 Java API —— ArrayList類 & Vector類 & Link

劍指offer---二叉樹和雙向鏈表

劍指offer 中序 logs style nbsp return public void cnblogs //肯定是要用中序遍歷。。。可是開始不怎麽會弄 //為什麽這麽菜 /* struct TreeNode { int val; struct Tr

章三 二叉樹和分制

最大 range swa return || sea 遞歸 tree zigzag 1 前序遍歷三種方式 非遞歸 1 public ArrayList<Integer> preorderTraversal(TreeNode root) {

LeetCode - 二叉樹的最大深度

解法 最大 span node bsp treenode turn roo div 自己解法，歡迎拍磚 給定一個二叉樹，找出其最大深度。 二叉樹的深度為根節點到最遠葉子節點的最長路徑上的節點數。 說明: 葉子節點是指沒有子節點的節點。 示例：給定二叉樹 [3,9,20,nu

二叉樹和二叉查找樹--數據結構與算法JavaScript描述(10)

高效 二叉查找樹 2層 連接 結構 數據結構與算法 計算 所有 二叉 二叉樹和二叉查找樹 概念 樹是一種非線性的數據結構，以分層的方式存儲數據。 樹被用來存儲具有層級關系的數據，比如文件系統的文件； 樹還被用來存儲有序列表。 一棵樹最上面的節點稱為根節點。 如果一個節點下

二叉樹和哈希表的優缺點對比與選擇

尋址 rac 二叉樹 得出 數據結構 個數 ron 之前 理論 二叉樹(binary tree)和哈希表(hash table)都是很基本的數據結構，但是我們要怎麽從兩者之間進行選擇呢？他們的不同是什麽？優缺點分別是什麽？ 回答這個問題不是一兩句話可以說清楚的，原因是在不同

二叉樹和雜湊表的優缺點對比與選擇

二叉樹(binary tree)和雜湊表(hash table)都是很基本的資料結構，但是我們要怎麼從兩者之間進行選擇呢？他們的不同是什麼？優缺點分別是什麼？ 回答這個問題不是一兩句話可以說清楚的，原因是在不同的情況下，選擇的依據肯定也不同。首先來回顧一下這兩個資料結構： 雜湊表使用hash functi

劍指offer——找出二叉樹和為n的路徑

連結串列和二叉樹比較難做，主要因其均以鏈相連線，.next and .left 來輸出結構中的資料，無法精確定位，所以通常用遞迴方法實現。 通過遞迴方法，本人感覺最重要的是確定.next的這部中具體實現的操作，然後逐漸實現遞迴。找出二叉樹和為n的路徑，就針對每一步做加和操作以及記錄路徑，並判

LeetCode-二叉樹的最大深度

.title { text-align: center; margin-bottom: .2em } .subtitle { text-align: center; font-size: medium; font-weight: bold; margin-top: 0 } .todo { font-famil

Leetcode 二叉樹的minimum Depth

已知一個二叉樹，求它的高。空樹的樹高是0，下面的樹的樹高是3。    遞迴地計算一個節點的左右子樹的樹高，將高度設值為兩個孩子最大高度加1。看下面的虛擬碼和程式的詳細情況。 演算法： package learn.java.cn.data.stru; cl

[Leetcode] 二叉樹的最小差

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x)

線索二叉樹和二叉樹基本操作的實現

2018-11-18-18:25:23 一：二叉樹 1.二叉樹的性質 　　①：在二叉樹的第i層上至多有pow(2,i-1)個結點(i>=1)。 　　②：深度為k的二叉樹至多有pow(2,k)-1個結點(k>=1)。 　　③：對任何一顆二叉樹T,如果其終端結點的個數為n0，度為2的結點數為

給定一個二叉樹和其中的一個結點，請找出中序遍歷順序的下一個結點並且返回。注意，樹中的結點不僅包含左右子結點，同時包含指向父結點的指標。

題目描述 給定一個二叉樹和其中的一個結點，請找出中序遍歷順序的下一個結點並且返回。注意，樹中的結點不僅包含左右子結點，同時包含指向父結點的指標。 /* 分析二叉樹的下一個節點，一共有以下情況： 1.二叉樹為空，則返回空； 2.節點右孩子存在，則設定一個指標從該節點的右孩子出發，一直沿著指向左

Leetcode---二叉樹的鋸齒形層次遍歷--思路

二叉樹的鋸齒形層次遍歷 題目連結：二叉樹的鋸齒形層次遍歷 解題思路： 思路上和普通層次遍歷沒有什麼區別，就多了一個偶數層翻轉集合順序 深度遍歷使用輔助棧結構，層次遍歷使用輔助佇列結構，java當中List結構也可以作為佇列使用 通過兩個數分別記錄當前層和下一層

【資料結構學習筆記】二叉樹和其他樹

基礎定義 一個樹t是一個非空的有限元素的集合，其中一個元素為根（root），其餘的元素（如果有的話）組成t的子樹（subtree） 樹的另一常用術語為級（level）。樹根是1級，其孩子（如果有）是2級，孩子的孩子是3級，等等。 一棵樹的高度（height）或深度（de